【統計力学9】量子力学への道【状態は離散的に】
箱の中の電磁場の問題を考えるところから,量子力学という分野が拓けました.ここでは,統計力学に関連して,量子力学の原理についても簡単に解説します.歴史的には電磁場の話以外にもさまざまな複雑な経緯があったので,ここで正確に量子力学の歴史をたどることはできませんし,私にそれを語る力もありませんが,どうして量子力学を導入しなければならないかというところは納得できるように話したいと思います.
エネルギー量子仮説
はじめに,調和振動子について,古典力学での取り扱いを復習し,問題点を振り返ります.
調和振動子のハミルトニアンは
$$
H(q,p) = \frac{p^2}{2m} + \frac{m\omega^2 q^2}{2}
$$
であって,トラジェクトリは図のようになります.
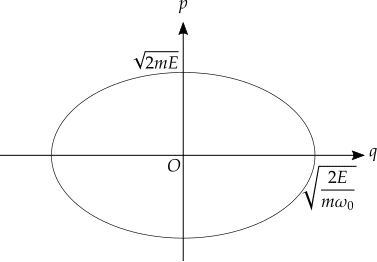
この場合はトラジェクトリは二次元に書けるので等エネルギー「線」になっていて,その囲む面積は
$$
\frac{2\pi E}{\omega}
$$
となっていることを後のために指摘しておきます.
調和振動子の古典的な分配関数を定義に従って計算すると,
$$
\newcommand{\explr}[1]{\exp\!\left(#1\right)}
\begin{align*}
Z(\beta) &= \int_{-\infty}^{\infty} \frac{dqdp}{h} e^{-\beta H} \\
&= \frac{1}{h} \int_{-\infty}^{\infty} \explr{-\frac{\beta p^2}{2m}} dp
\int_{-\infty}^{\infty} \explr{-\frac{\beta m \omega^2 q^2}{2}} dq\\
&= \frac{1}{h} \sqrt{\frac{2\pi m }{\beta}} \sqrt{\frac{2\pi kT}{m\omega^2}} = \frac{2\pi }{\beta h\omega} = \frac{1}{\beta \hbar \omega}
\end{align*}
$$
となるので,エネルギーの期待値は
$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\begin{align*}
E(\beta) &= -\pd{}{\beta} \ln Z(\beta)\\
&= \frac{1}{\beta} = kT
\end{align*}
$$
となり,エネルギー等分配則を得ます.電磁場は,空間が連続であることに由来して,無限個の調和振動子と同等であることがいえるので,エネルギー等分配則を箱の中の電磁場に適用するとエネルギーが無限大になってしまうというおかしなことになってしまうのでした.
ここで,ボルツマンの公式にも出てくる,状態数の数え方を思い出しましょう.状態数を数えるときは,位相空間において等エネルギー面の囲む体積を,プランク定数というもので割ることで無次元に合わせていました.プランク定数は最終的な計算結果には自由エネルギーの定数部分に現れるだけだったので,自由エネルギーの微分から求まる物理量には何も影響しません.古典力学的にはプランク定数は次元さえ合わせられれば何でもよかったのです.
ただ単に次元を合わせるためのプランク定数でしたが,本当にプランク定数で区切られる体積ごとに,とりうるエネルギーの値が離散化される(とびとびの値をとる)と考えてみます(これを初めて見出したのはボーズで,歴史的には本当はもう少し後のことです).つまり,
$$
\frac{2\pi E}{\omega} = nh\\
\therefore E = \hbar \omega n
$$
と考えて,エネルギーのとりうる値は
$$
n = 0, 1, 2, \ldots
$$
によってとびとびの値に制限されると考えるのです.ただし,$${\hbar = h/2\pi}$$としました.この今のところよくわからないアイデアを採用すれば,調和振動子の分配関数は,積分ではなく和に置き換わって
$$
Z(\beta) = \sum_{n=0}^{\infty} e^{-\beta \hbar \omega n} = \frac{1}{1 - e^{-\beta \hbar\omega}}
$$
と(等比数列の和の公式を使って)計算されます.するとエネルギーの期待値は
$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\begin{align*}
E(\beta,\omega) &= - \pd{}{\beta} \ln Z(\beta)\\
&= \hbar \omega \frac{e^{-\beta\hbar\omega}}{1 - e^{-\beta\hbar\omega}}\\
&= \frac{1}{\beta}\frac{\beta\hbar \omega}{e^{\beta\hbar\omega} - 1}
\end{align*}
$$
となります.この新しいエネルギー分配則では,エネルギーが温度だけでなく,調和振動子の周波数にも依存しているところがエネルギー等分配則とは違います.この式をプランクの分配則と呼びましょう.プランクの分配則は,高温または低周波の領域では,分母の指数を展開することにより,エネルギー等分配則に戻ることがわかります.
ではこの結果を,箱の中の電磁場のスペクトルを考えるのに当てはめてみましょう.箱の中の電磁場において,振動数が$${[\omega, \omega+ d\omega)}$$の間にある振動子の数は,単位体積当たり
$$
\frac{\omega^2}{\pi^2 c^3} d\omega
$$
となることが示せます.(これを示すのは省略しますが,簡単です.)したがって,箱の中の電磁場のエネルギーのスペクトルは,単位体積当たり
$$
u(\omega,\beta) = \frac{\hbar \omega^3}{\pi^2 c^3} \frac{1}{e^{\beta\hbar\omega} - 1}
$$
となります.これをプランクの公式といいます.
この式は実験とよく一致しています.プランクの公式によってプランク定数は初めて決められ,今ではその値は
$$
h = 6.62607015 \times 10^{-34}\ \text{J s}
$$
という定義値となっています.(2019年に単位系が改定され,プランク定数は定義値になりました.プランク定数を定義値とすることによって,これまで重さの単位の基準となっていたキログラム原器がお役御免になりましたね.)
また,周波数について足し上げれば,
$$
\epsilon(T) = \int_{0}^{\infty} d\omega\ u(\omega,\beta) = \frac{\pi^2 k^4}{15 c^3 \hbar^3} T^4
$$
を得て,エネルギー密度が温度の4乗に比例するというシュテファン・ボルツマンの法則を再現します.
プランクの公式の意味を考えるために,極限的な状況を考えてみましょう.プランクの公式において,低周波数の極限の領域のとき,つまり
$$
kT \gg \hbar\omega
$$
のとき,分母の指数を展開して
$$
u(\omega,\beta) \sim \frac{\omega^2}{\pi^2 c^3} kT
$$
と近似されます.これはレイリー・ジーンズ(Rayleigh-Jeans)の法則と呼ばれます.これは,電磁波を古典的な波動と考えて,エネルギー等分配則を適用した式になっています.逆に,高周波数の極限の領域のとき,つまり
$$
kT \ll \hbar\omega
$$
のときは,分母の1を無視して
$$
u(\omega,\beta) \sim \frac{\hbar\omega^3}{\pi^2 c^3} e^{-\beta\hbar \omega}
$$
と近似されます.こちらはヴィーン(Wien)の法則と呼ばれます.これは,エネルギーとして「エネルギー素量」$${\hbar\omega}$$をもつ古典的「粒子」がマクスウェル分布しているときの式になっています.
以上がどういうことかというと,エネルギー素量が大きい(周波数が大きい)ほど,エネルギーの不連続性が顕著になるわけです.そういうときは,たった一つでもエネルギー素量が分配されるだけでも,分配される確率$${e^{-\beta E}}$$が非常に小さくなって,ほとんど期待値には寄与しなくなるのです.このおかげで,周波数の大きい自由度は「死んで」しまって,エネルギーが無限大になることが回避できているのです.まわりの熱的環境に比べてエネルギー素量が十分小さい(周波数が小さい)とき,エネルギーはほぼ連続に扱ってよくなり,エネルギー等分配則によく従うことになります.
これは皆さんのお財布にたとえることができると思います.数百円の安い買い物をする(=環境の温度が低い)ときには,普通は小銭(=小さなエネルギー素量)で支払って,一万円札(=大きなエネルギー素量)は使わないでしょう.こういうときは一万円札は買い物に寄与しないということになります.
以上を振り返ると,実験に合う結果を導くうえで重要だった仮説は,
$$
E = \hbar \omega n
$$
という,エネルギーが離散的な値しかとらないというものでした.これをエネルギー量子仮説といいます.これは1900年にプランクが初めて提唱しました.
結晶の比熱
エネルギー等分配則に代わり,プランクの分配則が得られたので,これを用いて結晶の比熱の理論を作り直すことができそうです.
結晶を連続体と近似的にとらえると,振動数が$${[\omega,\omega+ d\omega)}$$の間にある固有振動の数は,単位体積当たり
$$
\newcommand{\lr}[1]{\left(#1\right)}
\frac{1}{2\pi^2}\lr{\frac{1}{c_l^3} + \frac{2}{c_t^3}} \omega^2 d\omega
$$
となります.光子気体の場合は二つの成分の横波だけでしたが,連続体を伝わる波は二成分の横波に加えて一成分の縦波もあるため,表式が少し異なります.縦波の速度を$${c_l}$$,横波の速度を$${c_t}$$としています.
ところで,結晶は本当は連続体ではないので,有限の自由度を持ちます.したがって,固有振動数の総数はその自由度に等しい,すなわち,固有振動数にはあるところに上限$${\omega_{\mathrm{max}}}$$があって,
$$
\newcommand{\lr}[1]{\left(#1\right)}
\int_0^{\omega_{\max}} \frac{1}{2\pi^2} \lr{\frac{1}{c_l^3} + \frac{2}{c_t^3}} \omega^2 d\omega = \frac{3N}{V}
$$
が成り立っていなくてはなりません.この上限よりも高い振動数の振動はないと考えます.この式から上限の固有振動数が求まります.
以上の考えをもとに,プランクの分配則を用いると,結晶の総エネルギーは
$$
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
E(T,V,N) &= V \int_0^{\omega_{\max}} \frac{\hbar\omega^3}{2\pi^2} \lr{\frac{1}{c_l^3} + \frac{2}{c_t^3}} \frac{1}{e^{\beta\hbar\omega} - 1} d\omega\\
&= 3 NkT D\lr{\frac{\hbar\omega_{\max}}{kT}}
\end{align*}
$$
と書けます.ここでデバイ関数は
$$
D(x) = \frac{3}{x^3} \int_0^x \frac{\xi^3}{e^{\xi} - 1} d\xi
$$
によって定義しました.デバイ関数の引数が小さいと1に近づき,大きいと0に近づく関数になっています.
結晶の総エネルギーの温度微分によってモル比熱を計算すると,
$$
\newcommand{\lr}[1]{\left(#1\right)}
c= 3N_A k \lr{4D\lr{\frac{\hbar\omega_{\max}}{kT}} - \frac{3 \beta \hbar \omega_{\max}}{ e^{\beta\hbar\omega_{\max}} - 1} }
$$
となります.固有振動数の上限値を定めれば,この式によって実験結果をよく説明することができます.ただし,固有振動数の上限値は物質によって異なる値を持ち,理論的に定めるのは困難です.理論から言える普遍的な法則は,温度が高い領域ではデュロン・プティの法則であり,温度の低いところでは比熱は温度の3乗に比例するということになります.(物理は極限的な状況を考えるのは得意ですが,物の性質を反映するような中間的なところを考えるのは苦手なところがあります.中間的なところは実際に実験してみるのが最も良い方法です.)
量子力学の定式化
エネルギー量子仮説の「状態が離散化される」という条件は,古典論の範囲で考えている限り,外から付加的に与えてやらなければいけないものです.これは単に古典力学にちょっと制限をつけるだけのものと考えても良さそうですが,実はそれではいけません.たとえば着目系と環境がエネルギーをやり取りするときを考えてみましょう.このとき,常にエネルギーが離散化されているためには,エネルギー素量$${\epsilon = \hbar\omega}$$を単位としてやり取りしなければならないはずです.しかし,古典力学では,電磁場のエネルギーは空間に連続に分布していて,しかもエネルギーの伝播速度は有限ですので,エネルギーの塊を瞬間的にやり取りすることは許されていません.ということは,エネルギーは空間に粒々に存在していて,その粒をやり取りすると考える必要があるわけですが,このような考え方は古典力学ではいくらひねっても出てくるものではありません.
後になって,光が粒々のようにふるまうと考えると,光が生成・消滅したりする現象,たとえば,光を金属表面に当てると電子が飛び出す光電効果という現象も,簡単に説明することができることがわかりました.身近な例を挙げると,ストーブでは日焼けしないのに,紫外線に当たると日焼けすることも,光が粒子のように振る舞うからと考えると簡単に説明できるとわかりました.しかし,これまで波であるとほとんど確信していた光が,実は粒子でもあったというおかしなことが起こってしまったのです.
現在では,光は波であるという立場から出発しても,粒子であるという立場から出発しても,実は全く同値であることがわかっています.つまり,もはや光が粒子なのか,波動なのかという質問に意味はなくなっています.よく粒子と波動の二重性といいますが,これらが二重に備わっているというのは誤解を招く表現だと思います.粒子とか波動とかいうものも,もとはといえば人間が考えたものですから,本性は別にどちらでもなくとも本当は不思議はないのです.
これは光に限らず,逆にこれまで粒子だと考えられてきた電子や陽子,中性子なども同様に,波動と思ってよいことが後々わかりました.こういうわけで,光もこれらの仲間として考えてよくなり,光の「粒子」を光子と呼ぶようになりました.
さて,エネルギー素量を表す式において,プランク定数は周波数とエネルギーを等置する奇妙な役割を果たしていますが,この意味でこの式は光の「波動性」を「粒子性」と結びつける式だということもできます.古典力学では,波動のエネルギーというのは,波の振幅の二乗に比例したものです.そして振幅は任意の値をとることができます.したがって,そこに粒子性を考慮に入れるのなら,振幅の大きさを離散化するなんらかの理論形式が必要になります.
状態が離散化される,このどうしても必要な条件をあらかじめ物理量の性質として数学的な構造の中に組み込んでしまったのが量子力学(quantum mechanics)です.これがどのような理論かというと,位置や運動量はただの数ではなくて,
$$
p(t)q(t) - q(t)p(t) = -i \hbar
$$
を満たすような行列だというのです(ただの数だとしたら掛け算の順番を変えても同じなので上は0になってしまいますが,そうではないといっています).ちなみに,この左辺をよく
$$
[p(t), q(t)]
$$
と記して交換子(commutator)といい,上の関係は正準交換関係(canonical commutation relation)といいます.
物理量が行列で表されるなら,私たちが観測する実数の世界の物理量は何なのかと思われると思います.実は,量子力学の構造は次のようになっています.まず,量子力学的に許される状態(量子状態)というのは,物理量(行列で表されている)の固有ベクトルたちです.それぞれの固有ベクトルの属している固有値は,その量子状態を観測すると実際に現れる物理量(実数値をとる)です.そして,実際に私たちがマクロな世界で観測するのは,各量子状態の持つ固有値を確率的に足し合わせた期待値なのです.
系の運動方程式はやはり正準方程式
$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\begin{align*}
\dot{p}_i &= - \pd{H}{q_i}\\
\dot{q}_i &= \pd{H}{p_i}
\end{align*}
$$
で与えられると考えることにします.すると行列関数の偏微分の形となっていて,恐ろしく見えますが,行列関数の偏微分も,ただの数の偏微分と同様にして定義できます.行列関数の偏微分をうまく定義して,さらに先ほどの正準交換関係を仮定すると,結局,正準方程式は交換子を用いて書くことができて,
$$
\dot{p} = \frac{i}{\hbar} [H, p]\\
\dot{q} = \frac{i}{\hbar} [H, q]
$$
という形になることが数学的に示せます.さらに一般の物理量についても,
$$
\dot{f} = \frac{i}{\hbar} [H, f]
$$
という美しい形に書けることが示せます.これをハイゼンベルグ(Heisenberg)の運動方程式といいます.ハイゼンベルグの運動方程式が,量子力学の基礎方程式となります.
「物理量が行列で表されること」と,「ハイゼンベルグの運動方程式」とを要請することから,エネルギーが量子化されることを次に簡単にお話します.
調和振動子の量子化
さて,まずはハイゼンベルグの運動方程式を用いると,古典力学での調和振動子の運動方程式と同等のものを再現することを確かめておきます.
調和振動子のハミルトニアンはやはり
$$
H(q,p) = \frac{p^2}{2m} + \frac{m\omega^2 q^2}{2}
$$
で,これをハイゼンベルグの運動方程式に入れると
$$
\begin{align*}
\dot{p} &= \frac{i}{\hbar} \frac{m\omega^2}{2}[q^2, p]\\
&= \frac{i}{\hbar}\frac{m\omega^2}{2} (q[q, p] + [q, p]q)\\
\dot{q} &= \frac{i}{\hbar} \frac{1}{2m} [p^2, q]\\
&= \frac{i}{\hbar} \frac{1}{2m} (p [p, q] + [p, q] p)
\end{align*}
$$
と変形できます.
ここに位置と運動量が正準交換関係を満たす行列であると仮定すると,
$$
\dot{p} = - m\omega^2 q \\
\dot{q} = \frac{p}{m}
$$
となり,古典力学の運動方程式と同じ形のものが得られます.(ただし,古典力学の調和振動子の運動方程式と同じものを得るために満たすべき交換関係やハミルトニアンはこれに限らないことが知られています.その場合は,また異なった粒子の性質が現れてきますが,またそれは次回のお話.)
ところで,
$$
a = \sqrt{ \frac{m\omega}{2\hbar} } q + \frac{i}{\sqrt{2m\hbar \omega}} p,\\
a^{\dagger} = \sqrt{ \frac{m\omega}{2\hbar} } q - \frac{i}{\sqrt{2m\hbar \omega}} p
$$
によって無次元の量を定義すると,正準交換関係はこれらに対しては
$$
[a(t), a^{\dagger}(t)] = 1
$$
と同等であることを導けます.するとハミルトニアンは
$$
\newcommand{\lr}[1]{\left(#1\right)}
H = \hbar \omega \lr{a^{\dagger}a + \frac{1}{2}}
$$
と一つの物理量
$$
a^{\dagger}a = n
$$
によって書くことができます.この物理量を数演算子(number operator)と呼びます.そして,数演算子の固有値は
$$
n = 0,1,2,\ldots
$$
と整数になることが導けます.したがって,このように量子力学で調和振動子を扱うと,振幅は任意の値をとることはなく,離散的な値しか取れないことになるのです.
もちろん,この話だけで量子力学が正しいとするのは証拠不十分ですが,数々の実験が量子力学の正しさを裏付けています.(歴史的には,原子の発光スペクトルから,軌道の遷移の理論を着想し,それと古典力学との対応原理に導かれて量子力学を徐々に整備していった...という感じです.)
今回のまとめ
統計力学の問題から量子力学が生まれた.量子力学によると状態は離散化される.状態が離散化されると考えると,プランクの分配法則という実験によくあう法則が得られる.光は波動と粒子の両方の側面を持つこともわかったが,それは数式上は振動数と振幅のことで,振幅のとりうる大きさが量子力学によって制限されることになっている.
おまけ: 量子力学を学びたい人のために
量子力学に関してここでは深くは扱わなかったので,参考文献を挙げておきたいと思います.(いつか私の記事でもまとめたいですが...いつになることやら...)
まず,プランクの公式に始まり,昔の天才物理学者たちがいかにして苦労して量子力学なる枠組みを組み上げていったのかがわかる名著として朝永先生の『量子力学』があります.この記事を書く際にも大いに参考にしました.
この本は,I・IIの二巻+補巻『角運動量とスピン』の全三巻からなる教科書でして,全て読むのはかなり大変ですが,量子力学の理論の必然性がわかり,また,どうやって理論を組み立てていくんだろうと読んでいて非常にワクワクします.ただし,このワクワクはミステリー小説を読むときのワクワクに近いのかもしれません.つまり,最後まで読まないと犯人が分からないのと同様に,この本は最後まで読まないと量子力学の正しい理論がわからないのです.ミステリー小説でネタバレは面白さ半減ですが,すでに完成された物理の理解を目的とするときは,逆に早くネタバレしてくれた方が効率よく楽に学べるものです.この本ではじわじわと理論を作っていくので,かなり難しいし,最後まで読む前に挫折するのが普通だと思います.ですから,初めて量子力学を学ぶのに読む本としては効率が悪く,おすすめしません.それでも,別の教科書を使って量子力学の理論体系をネタバレしておいてから学ぶ本としては,なんといってもとても面白いのです.物理はネタバレしても面白さは変わらないどころか,理論を完成させた学者に対する尊敬をもって,かえって楽しく学べる気がします.
さて,効率よく量子力学をネタバレするためにおすすめの本は,清水明さんの『量子論の基礎』やJ. J. サクライの『現代の量子力学』が簡潔でわかりやすいと思います.まずはこちらで学ぶのがよいと思います.
清水さんの本もサクライの本も基礎がわかるように深いところから書かれていると感じます.
ちなみに,私は実は化学専攻の人間なので,初めて量子力学を学んだのは物理化学の教科書でした.物理化学の教科書というのは,物理の教科書と違って,原子や分子の性質を説明するために「量子力学を使っていく」イメージの教科書が多いので,私はしばらくはわけがわからないまま量子力学を使っていました.そんな中,P. Atkinsの“Molecular Quantum Mechanics”は量子力学も誤魔化しなしに書かれていて,よかったです.
英語が得意でないくせに,院試勉強もこの本でしました.しかし英語で書かれていると精読しようとするのでかえってきちんと理解するのによかったのかもしれません.また,この本には結構な間違いが含まれていたと思います.さすがに教科書に間違いはないに越したことはありませんが,教科書が間違っている気がして色々調べるのも勉強になることがあります.(特に群論の章で,大直交定理を既約ユニタリ表現でないものに適用していますが,これはおかしいので注意が要ります.)
ところで,この本の表紙はかっこいい.なんと,表紙の数式はやや立体的になっていて,さらに光沢のある加工がされていて,光の反射で数式が浮かび上がるようになっています!
______________________
2020. 08. 14 執筆
2020. 08. 28 ご指摘のあった光電効果と光子に関する説明を修正しました
2020. 11. 27 アトキンスの書評を修正
いいなと思ったら応援しよう!

