【統計力学５】カノニカル分布【温度で指定された系】

熱力学では，温度と外部変数で状態が指定されました．このときの状態を記述するような統計力学的なモデルを得ることが今回の目標です．

熱的に接触した系の運動

温度で状態を指定したいので，前回に引き続き，議論の出発点として着目系と環境が熱的に接触した系を考えます．

着目系と環境を合わせた全系は孤立系として運動するとすると，全系は等エネルギー面上を運動します．しかし，着目系の運動のみを見ると，着目系は環境とエネルギーをやりとりしますから，もはや運動は等エネルギー面上に限られません．環境の情報を縮約してしまう結果，いろいろなエネルギーに対応する領域を確率的に運動することになります．

今考えている理論枠組み（平衡統計力学の枠組み）では，詳細なダイナミクスは必要ないので，代表点の確率分布を調べるだけでよく，比較的簡単に考えることができそうです．

カノニカル分布の導出

前回，全エネルギーは決まっているとき，着目系があるエネルギーをとる確率を次のように与えました．

このとき，着目系の位相空間上のある点に系が見いだされる確率は，

に比例することになります．着目系のミクロな状態を一つに決めても，環境のミクロな状態がいろいろな状態をとってよいので，確率は環境の状態数に比例するわけです．エネルギーを独り占めするような状況ほど，起こりづらくなるような分布になっています．

着目系のエネルギーが全体のエネルギーに比べて小さいとして，対数をとってテイラー（Taylor）展開すると

となります．（補足: テイラー展開をここまでで打ち切ってよいことは

このようにオーダーを確認すると確かめられます．環境の粒子数が大きい極限で二次以上の項を無視できます．）

これを再び指数をとってやると，（テイラー展開の第一項はただの定数なので指数をとれば比例に押し込めてよくて，）

という分布が得られます．エネルギーが高いほど指数関数的に見出す確率が低くなるような分布です．ただし，ここで前回得られた要請

を使いました．（このように環境の温度を用いて系の温度とするために，大きな環境に小さな着目系が浸かっているような状況で考察をしたのです．）この分布をカノニカル分布（canonical distribution）といいます．

今のところ，確率分布の比例関係だけを得たわけですが，確率分布であるからには，確率変数（ここでは位相空間上の位置）について和をとると１になっていなくてはなりません．規格化定数を

と置けば，カノニカル分布は

と書けます．この規格化定数のことを分配関数（partition function）と呼びます．またはより古い呼び名で状態和ということもあります．この分配関数はただの規格化定数のように思えますが，実は分配関数には系の情報がすべて詰まっています．そのことは次回見ることにしましょう．

（余談: カノニカルという言葉は，音楽のカノンと同じ語源です．カノンには規範という意味があります．カノニカル分布は統計力学でもっとも有用に用いられる分布だからこのように名付けられたのでしょう．

それから，分配関数という名前はおそらく，エネルギーを着目系と環境とで分配したときの場合の数（状態数）の考察から得られたものなので，このような名前なのだろうと思いますが，あまりしっくりきません．

語源はつい気になってしまいますが，物理用語は当時の物理学者が苦心してつけたものであって，自然の本質を表しているとは限りませんから，あまり気にしないほうがよいと思います．ちなみに，Ｘ線も当時正体不明だったのでＸ線と名付けられ，その名前が定着してしまったものです．物理は難しいので，ぴったりとくるような良い名前を付けるのも確かに難しいことですね．）

ミクロカノニカル分布とカノニカル分布の等価性

ミクロカノニカル分布は，次の図のように，等エネルギー面上に代表点が一様に分布したものでした．

一方，カノニカル分布は，次の図のように，あらゆるエネルギーをとりえますが，それぞれの代表点を取りうる確率は，エネルギーが高いほど減少していくような分布です．

一見，系が孤立しているか開放しているかによって，異なる分布を考えなければならないように思えます．しかし，平衡状態とは，いったん達成されてしまえば，部分系を切り離して孤立させても，同じ温度の環境の中に浸けても，なにも起こらない状態です．平衡状態は孤立していようがしていまいが同じことです．したがって，ミクロカノニカル分布も，カノニカル分布も同じ状態を記述するものでなければなりません．

しかし実際に，ミクロカノニカル分布とカノニカル分布が同じ状態を記述することは，前回見た次の図

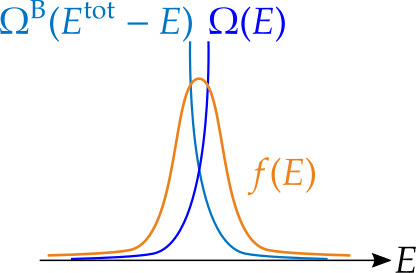
からほぼそのまま理解することができます．つまり，カノニカル分布で計算しても，平衡状態のエネルギーの値のところに鋭いピークを与えるので，結局ミクロカノニカル分布と同じ状態を記述していると言えるのです．

ちょっとしたたとえ話をしてみます．お金がありすぎて困る人はいないと思います．お金がたくさんあれば色々なものが買えて可能性が広がりますから，みんなお金持ちになりたいと思うわけです．（幸せはお金に依存しないという意見もあるでしょうし私はそれに賛成ですが，本ノートの範囲を超える問題です...）しかし，実際には億万長者はごく限られた人しかなれません．逆に，お金が全くないという人は何も買えず，生きていくことができませんから，そういう人もほぼいないでしょう．それで，ほとんどの人はみんな似たり寄ったりの収入でやりくりしているのです．お金をエネルギーと思うと，今の話はカノニカル分布がミクロカノニカル分布と一致する理由と似ています．

（余談: このたとえ話では「景気」のようなものが温度に対応するような気がなんとなくします．また「利潤最大化」のような原理が熱力学の自由エネルギー最小原理（またはエントロピー最大原理）と対応するような気がします．しかし私は経済学を何も知らないので，これ以上深入りするのはやめておきます．経済学を熱力学や統計力学と結びつけるような研究はあるのでしょうか？私は知りませんが，ミクロ経済学やマクロ経済学という言葉を聞いたことはありますし，自然な発想としてありそうな気はします．詳しい方がいたら教えてください．）

ミクロカノニカル分布もカノニカル分布も与える物理量の計算結果は同じです．それでは何が違うのかというと，考えている系の違いというよりも，系の状態の指定の仕方が違うのです．ミクロカノニカル分布はエネルギーで状態を指定しているのに対して，カノニカル分布は温度で状態を指定して物理量を計算するための分布です．ミクロカノニカル分布が実際の分布を表すわけではなかったのと同様に，カノニカル分布も実際にの分布しているわけではないと思っておくのが正しい．私たちは温度を制御して実験をすることが多いから，カノニカル分布を便利に用いて計算をするというだけです．

今回のまとめ

カノニカル分布は温度で指定された系の状態を記述する分布であり，エネルギーで指定された系の状態を記述するミクロカノニカル分布と同じ計算結果を与える．