4次元版マンデルブロ集合を見てみたかった

2023年1月22日 19:00

どうも、108Hassiumです。

ある時ふと、こんなことを思いつきました。

以下の数列が無限大に発散しないような$${(c_v,c_w,c_x,c_y)}$$($${\in\mathbb{R}^4}$$)全体の集合を可視化できないか？
$${\begin{cases}v_{n+1}=v_n^2-w_n^2-x_n^2+y_n^2+c_v&v_0=0\\w_{n+1}=2v_nw_n-2x_ny_n+c_w&w_0=0\\x_{n+1}=2(v_nx_n-w_ny_n)+c_x&x_0=0\\y_{n+1}=2(v_ny_n+w_nx_n)+c_y&y_0=0\end{cases}}$$

数式だけ見てもなんのこっちゃ分からないという人が多いと思いますので、順を追って説明します。

まず、マンデルブロ集合は以下の複素数列が無限大に発散しない複素定数$${c}$$全体の集合です。

$${z_{n+1}=z_n^2+c　z_0=0}$$

$${z_n=a_n+ib_n}$$、$${c=c_a+ic_b}$$とすると$${z_{n+1}}$$は以下のように表され、マンデルブロ集合は以下の数列が無限大に発散しない実数の2つ組$${(c_a,c_b)}$$全体の集合となります。

$${\begin{cases}a_{n+1}=a_n^2-b_n^2+c_a&a_0=0\\b_{n+1}=2a_nb_n+c_b&b_0=0\end{cases}}$$

ここでさらに、$${a_n}$$と$${b_n}$$を複素数に拡張し、$${a_n=v_n+iw_n}$$、$${b_n=x_n+iy_n}$$、$${c_a=c_v+ic_w}$$、$${c_b=c_x+ic_y}$$とすると$${a_{n+1}}$$と$${b_{n+1}}$$の式は以下のように書き換えられます。

$${\begin{cases}v_{n+1}=v_n^2-w_n^2-x_n^2+y_n^2+c_v&v_0=0\\w_{n+1}=2v_nw_n-2x_ny_n+c_w&w_0=0\\x_{n+1}=2(v_nx_n-w_ny_n)+c_x&x_0=0\\y_{n+1}=2(v_ny_n+w_nx_n)+c_y&y_0=0\end{cases}}$$

これこそが冒頭の式です。

そして、この数列が無限大に発散しないような$${(c_v,c_w,c_x,c_y)}$$全体の集合こそが「4次元版のマンデルブロ集合」と呼ぶにふさわしいと考え、その姿を見てみたいというのが冒頭で述べた「思い付き」の真意でした。

というわけで、4次元マンデルブロ集合の可視化を試みました。

2Dスライス

まずは、4つの変数の内２つを固定して2Dの画像として描画してみることにしました。

描画方法は以下の記事に書いてあるものと大体同じです。(ほぼ変数を増やしただけです)

定義上、これは明らかに普通のマンデルブロ集合と同じです。

$${c_w}$$を少しずらしてみました。

左側の円形の領域が変形していたり右側の谷が2つに分裂していたりするのが目立ちますが、それ以外にも細部をよく見ると枝状の部分が消えかかっていたりと微妙な違いがあります。

$${(c_v,c_x)=(-0.1,0.8)}$$付近の拡大図です。

枝は途切れ、円状領域は裂け、左下の方の飛び地はもはや訳が分からない状態になっています。

$${c_y}$$の方をずらしてみました。

$${c_w}$$をずらした方と同様に、普通のマンデルブロ集合の一部を切って別の部分とくっつけたような形に見えます。

$${c_w}$$と$${c_y}$$を両方動かしてみたら、対称性が崩れました。

アニメでよくある(?)「斬られてから数秒後に人体がバラバラになるシーン」みたいですが、切り口からも円状領域が生えているのを見ると斬られた方も只者ではなさそうです。

$${c_v}$$と$${c_w}$$を固定してみました。

多項式関数のマンデルブロ集合として普通にありそうな感じの、地味な形状です。

何の面白みもない正方形になってしまいました。

この形(といってもただの正方形ですが)、実は「分解型複素数のマンデルブロ集合」と全く同じ形です。

分解型複素数とは$${j^2=1}$$を満たす1でも-1でもない数$${j}$$と2つの実数$${a,b}$$を用いて$${a+bj}$$と表せる数のことです。

普通の複素数と同様に分解型複素数でも加法と乗法が定義でき、$${z_{n+1}=z_n^2+c}$$という数列の分解型複素数版は以下のようになります。

$${\begin{cases}a_{n+1}=a_n^2+b_n^2+c_a\\b_{n+1}=2a_nb_n+c_b\end{cases}}$$

説明は省きますが、4次元マンデルブロ集合の式は$${w_n=x_n=c_w=c_x=0}$$とすると上記の式と同じ形になり、先程の図形が分解型複素数のマンデルブロ集合と同じであることがわかります。

先程と同じく真っ黒い正方形が現れましたが、先程と違って周りに模様があります。

$${c_w}$$を連続的に動かしてみました。

真ん中の水平な線から上下に向かってマンデルブロ集合がスライドして出入りするだけに見えますが、よく見ると真ん中から離れた位置の構造も少しだけ動いています。

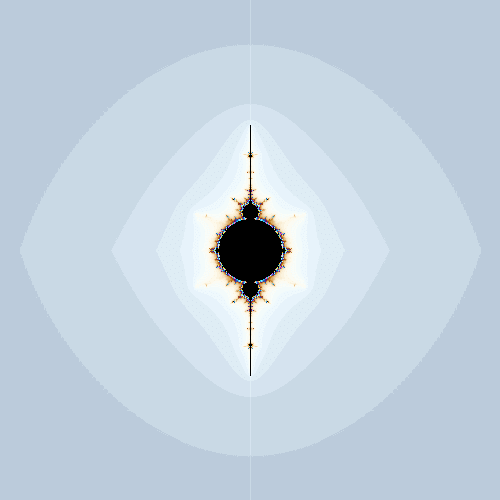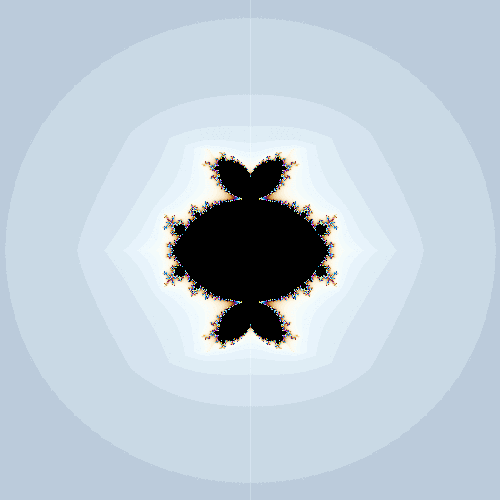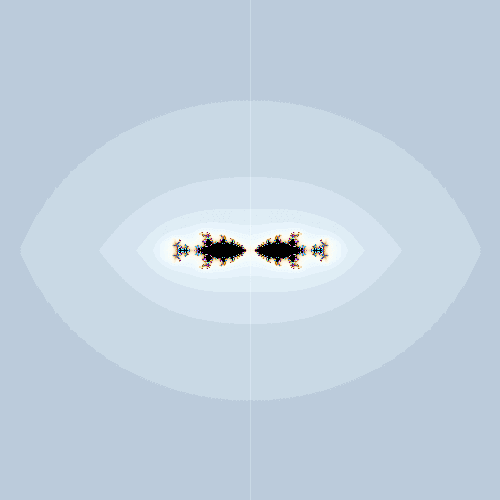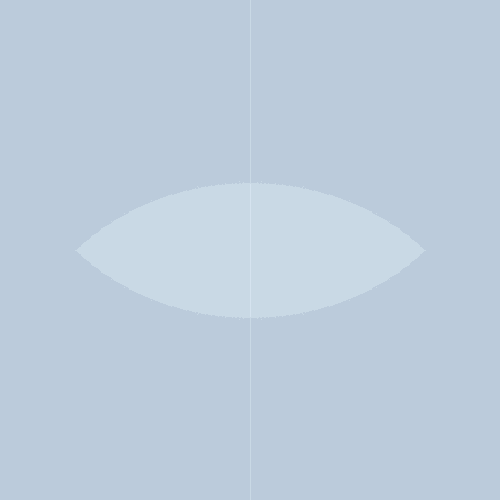
3Dスライス

2Dだとどんな形をしているのかよくわからなかったので、次元を一つ上げて3Dでの描画に挑戦してみました。

Processingで立体図形を描画する方法はよくわからなかったので(というか3DCGを勉強したことが一切ない)、完全に自己流のやり方で描画しました。

一応ソースコードを貼っておきますが、正直に言うとあまり参考にしないほうが良い気がします。

void setup(){
  size(1000,1000);
  colorMode(HSB);
  background(0);
  noStroke();
  int maxc,d,dmax;
  double v,w,x,y,pv,pw,px,py,cv,cw,cx,cy;
  boolean o,p;
  for(int a=0;a<1000;a++){
    for(int b=0;b<1000;b++){
      maxc=0;
      dmax=0;
      o=true;
      for(int c=0;c<1000&&o;c++){
        pv=(double)a/250.0-2.5;
        pw=(double)b/250.0-2.0;
        px=(double)c/250.0-2.0;
        cv=((pv*cos(-0.5)-px*sin(-0.5))*cos(0.5)-pw*sin(0.5))*0.7;
        cw=(pw*cos(0.5)+(pv*cos(-0.5)-px*sin(-0.5))*sin(0.5))*0.7;
        cx=(px*cos(-0.5)+pv*sin(-0.5))*0.7;
        cy=0;
        v=0;
        w=0;
        x=0;
        y=0;
        o=false;
        p=true;
        for(d=0;d<50&&p;d++){
          pv=v;
          pw=w;
          px=x;
          py=y;
          v=pv*pv-pw*pw-px*px+py*py+cv;
          w=2.0*pv*pw-2.0*px*py+cw;
          x=2.0*(pv*px-pw*py)+cx;
          y=2.0*(pv*py+pw*px)+cy;
          if(v*v+w*w+x*x+y*y>100){
            o=true;
            p=false;
          }
        }
        if(dmax<d){
          maxc=c;
          dmax=d;
        }
      }
      fill(cr(dmax/2.0),255,sh((float)maxc/500.0)*255);
      rect(a,b,1,1);
    }
  }
}

float cr(float c){
  return (c%256)*(256-(c%256))/65;
}

float sh(float c){
  return 1.0/(c*c*c*c+1.0);
}