
ノイマンのセル・オートマトン
どうも、108Hassiumです。
セル・オートマトンといえばいわゆる「コンウェイのライフゲーム」だけがやたらと有名ですが、実はセル・オートマトンの歴史はライフゲームが発表されるずっと前から続いており、ライフゲームよりも古いセル・オートマトンのルールがいくつも存在します。
そんな中でも特に古い(最古ではないらしいです)のが、「Von Neumann cellular automaton(ノイマンのセル・オートマトン)」です。
ざっと調べてみたところ、このルールの面白さについて日本語でわかりやすく解説している無料の資料は見つけられなかったのでこの記事で解説したいと思います。
歴史
ノイマンのセル・オートマトンは、1950年頃に数学者のジョン・フォン・ノイマンによって考案されました。
ノイマンは当時機械の自己複製について研究しており、自己複製が可能な機械のモデルを作るためにノイマンのセル・オートマトンを考案したようです。
当時はまだ実用的なコンピュータが開発される前でしたが、ノイマンは紙の上の計算だけで約20万セルの自己複製物体を設計したそうです。
ちなみにノイマンといえば、信じられないような計算能力の持ち主として数々の逸話が残っています。
先程の自己複製物体の話もその一つですが、実用的なコンピュータが開発された後ではコンピュータとの計算勝負に勝ち「俺の次に計算が速い奴ができた」と言った、というエピソードが有名です。
Gollyでの扱い
ノイマンのセル・オートマトンは、Gollyでは「JvN29」というルール名で登録されています。
※☟Gollyの基本的な使い方は以下の記事に書いてあります。
「Control」→「Set Rule」で出せるルール欄に入力することで設定できるほか、「Set Algorithm」から「JvN」を選択した際も自動的にJvN29が選択されるようになっています。

ルールをJvN29に設定すると画面はこのようになります。

このままパターンの作成をすることもできますが、このままセルを置いていくとどれが何のセルかわからなくなります。

この状態で下図のアイコンをクリックすると、セルの表示が見やすいものに切り替わります。

以下、セルの表示はこの形式にしたまま解説します。
また、ルール名も「ノイマンのセル・オートマトン」ではなく「JvN29」を使うことにします。
定義
JvN29の定義は非常に複雑なので、略式かつ少し変則的な説明の仕方をします。
9~12

9番から12番までの4種類セルは、信号(後述)を伝達させる導線の役割を持ちます。
アイコンが矢印型であることからわかる通り、信号の伝達方向はセルの種類ごとに固定されています。
13~16

13番から16番のセルは、導線の中を移動する信号として機能します。
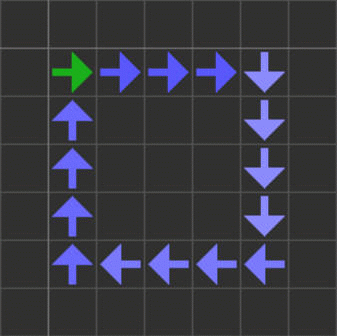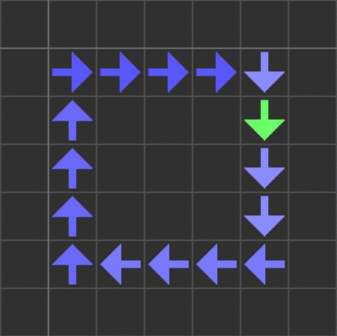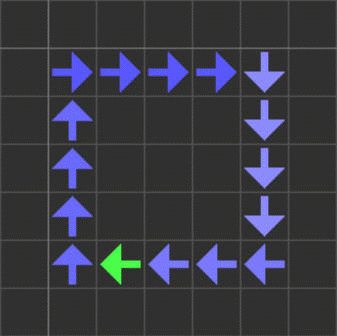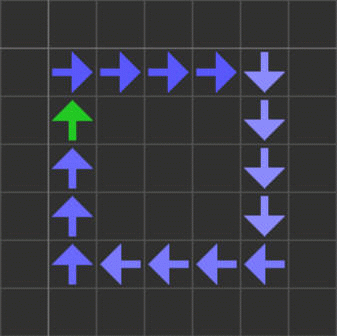
なお、JvN29の近傍形状はライフゲームと同じムーア近傍(カドを含む8セル)ではなく4セルの「ノイマン近傍」なので、斜め方向に接しているセルには信号は伝達しません。
17~20,21~24

17番から20番と21番から24番までのセルは、9~12と13~16と同様に「導線と信号」として機能します。

各導線と信号は違う色の方の導線セルを消去する機能があり、導線の末端に信号が到達するとその先にある違う色の導線を消せます。
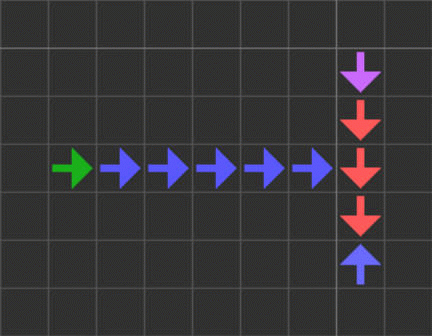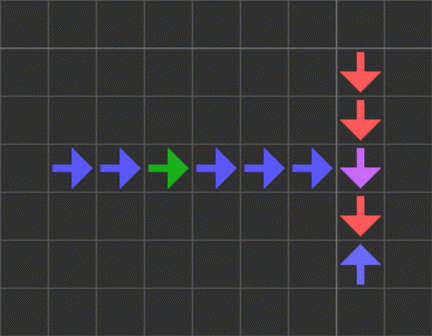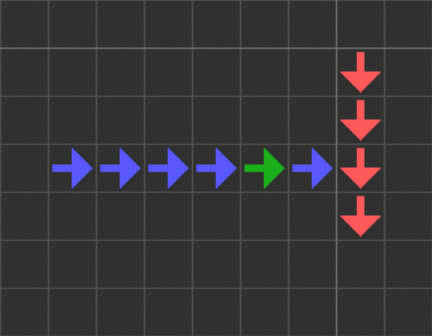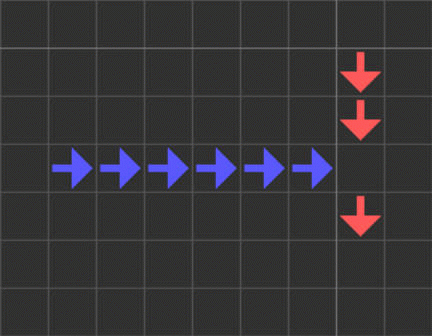
25~28

25番から28番までのセルは、導線の分岐点として機能します。

また、信号の伝達を遅延させる役割もあります。

さらに、「信号が流れ込む導線が複数本存在するときは、全ルートから同時に信号が流れた時しか信号が通らない」という仕様もあります。

なお、これらの仕様は青い導線から信号を受け取る時しか適用されず、赤の導線から信号を受け取ることはできないようです。

また、青線と25番セルどうしでの信号のやり取りはできるものの、25番セルどうしで直接信号を伝達させることはできません。
1~8

1番から8番までのセルは、新たなセルが生まれるときの中間状態のようです。

導線の端に信号が到達すると1~8番のセルが生まれ、信号の中身によって違うセルへと変化していきます。
どのセルがどの信号によって生成されるかわかっていないとこのルールで遊ぶのは困難ですが、かといって1~8番のセルの変化規則を覚えるのは大変です。
なので、私は先ほどのGIFのパターンを編集中のパターンファイルに貼り付けておき、必要な時にいつでも見られるようにして作業をしています。
パターン例
このルールでどんなパターンが作れるかを紹介します。
カウンター
2色の導線と分岐セルをうまく組み合わせることで、比較的簡単な構造でN進カウンターを作ることができます。

この2進カウンターはシンプルさを意識したためこんな形になっていますが、一般のN進法の場合は以下のような形になります。

建築アーム
以下のようなパターンを使うと、他のパターンを自動的に建築(?)するパターンを作ることができます。

左側に延びている導線から右側の部分に信号を送ることで、アームを伸縮させたり任意の位置にセルを置いたりといった動作ができます。

x = 47, y = 11, rule = JvN29
37.I2MIMpA4Q$37.4IMpA4I2$14.IMIM3IMI3MI2MI3MIM3IM2IMpA4Q$14.IM5IM14I
2M3IMpA4I2$7.IM7I3MI2MI3MIM6I6MIMpA4Q$7.I2M3I2M14I2M2I2M2IM3IMpA4I2$
12I2MIMIM5I3MI2MI3MIM3IM2IMpA4Q$4IM4IMIMIMIMIMI3M14I2M3IMpA4I!これを利用することで、例えばドット絵を無限に描き続けるパターンが作れます。
#セル・オートマトン
— 108Hassium (@1Hassium) November 3, 2019
ンョ゛ハー ゛ pic.twitter.com/rQKf1ttFem
また、少々変則的なパターンとして以下のようなものがあります。
#セル・オートマトン
— 108Hassium (@1Hassium) August 27, 2020
いのちの輝き pic.twitter.com/9mHiZ9wo9D
#のば描き#セル・オートマトン pic.twitter.com/77Hsb0xC8t
— 108Hassium (@1Hassium) July 26, 2021
この2つでは、描画するパターンと建築アームが一体化しています。
なお、セルの配色は下図の位置をダブルクリックすることで変更できます。

建築アームの変種として、以下のようなものがあります。

アーム自体の構造はほぼ同じですが、アームに送るコードを格納するテープが1本だけになっています。
アームを構成する上下2本の導線に全く同じ信号を送りつつ違う動きをさせなければならないので、使いこなすのはかなり難しいです。
利用方法は後述しますが、動作コードを書くだけでもパズル的で結構楽しいです。
無限増殖物体
ライフゲームのような「人口生命体シミュレータ」でないルールだと意味合いが変わってしまう気もするのですが、無限にセルが増え続けるパターンを作るのも結構面白いです。
このルールにおける最小の無限増殖物体は、おそらく以下の5セルのパターンです。
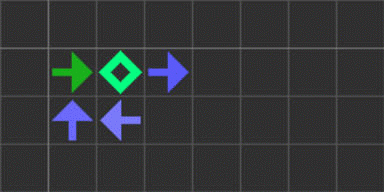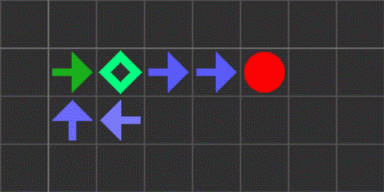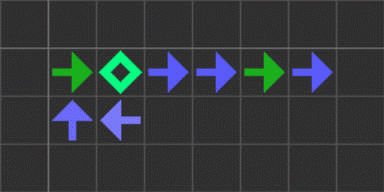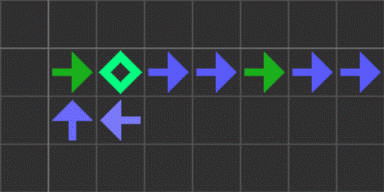
建築アームでこのパターンを作ることで、breeder(時間の2乗のオーダーで増殖する物体)ができます。


このパターンの初期セル数は672セルもあるのですが、改良を重ねたところ72セルのbreederを作ることができました。

複雑な形の物体を生成するbreederを作る際は、単テープ建築アームが役立つことがあります。

9999999999999999999999999
9999999999999999999999999
9999999999999999999999999
9999999999999999999999999
9999999999999999999999999
普通の建築アームを作る場合、作った建築アームを動かすためには2か所に同時に別々の信号を送る必要があるので設計に工夫が必要になります。
breeder以外にも、$${O(\sqrt{t})}$$や$${O(\text{log}(t))}$$などの変則的な成長速度を持つ物体を作ることができます。


ライフゲームと比べると、グライダーのような小さい移動物体が存在しない代わりに2進カウンターや信号ループ、建築アームのような便利なツールを作りやすいため、複雑なパターンを作りやすいです。
自己複製物体
ここまでで紹介したパターンはほぼ自作のものでしたが、ここからはGollyのサンプルパターンに入っているものを紹介します。
バージョン4.2では、JvN29のサンプルパターンは「Patterns」の中の「Self-Rep」の中の「JvN」というフォルダの中に入っています。

まず、これが「sphinx.mc.gz」というファイルの中身です。

右下の方にある点線がプログラムのコードの役割を持ち、建設アームとは異なった構造の読み取りアームで点の有無を読み取り、スフィンクスのような形の部分で読み取り結果を変換して右上の建築アームに送って自己複製を行う、というような仕組みになっているようです。
機械上の部分が非常に複雑なうえに、右下から画面外へ伸びているのコード部分が非常に長く総セル数は13万を超えています。
ちなみに動作は恐ろしく遅いようで、約2.6×10¹¹世代経過してようやく1回目の自己複製を終えたところのデータが「sphinx-spark.mc.gz」という名前で収録されています。

続いて、「JvN-loop-replicator.rle.gz」というファイルの中身がこちらです。

何やら文字がたくさん書いてあるのが目につきますが、そもそも構造がスフィンクスと全く違うのがわかると思います。
機械部分が小型化されているのは勿論のこと、よく見ると右下のコード部分が点線ではなくなっています。
ファイル名に「loop」と書いてある通り、このパターンでは点線の代わりに信号ループを使ってコードを管理しているようです。
ループ内のコードを機械部分で読み取って建築アームを動かし、機械部分だけを複製し、複製が終わったら機械部分に組み込まれたカウンターを動かしてループを作成し、それが終わったらコードをコピーしてループの中に格納する、という順序で自己複製を行っているっぽいです。
点線の読取機構等が要らなくなったためか機械部分は小型化されましたが、コード自体は長くなったようで総セル数は420万(文字部分を除くと丁度ではなくなる)となっています。
そして最後に、「small-JvN-self-replicator.rle」を紹介します。

これは見ての通りめちゃくちゃ小型化された自己複製物体です。
データ形式はJvN-loop-replicatorと同じループを用いているにもかかわらず、機械部分もコードも大幅に短縮され、総セル数は何と僅か24866セルです。
ところで、wikipediaの「セル・オートマトン」のページには「ノイマンは20万セルの自己複製物体を設計した」という記述がありますが、上記の3つの自己複製物体の初期セル数はどれも20万セルからは離れた値で、実際にノイマンが設計したものとは別物なのかもしれません。
コンピュータ


コンピュータができていた。
なお何の計算をしているのかは不明ですが、計算速度はかなり遅いようです。
