生死等価セル・オートマトン
どうも、108Hassiumです。
皆さんは「Day and Night」という名前のセル・オートマトンをご存知でしょうか。
※日本語版の記事は無いようです。
Day and Nightはライフゲームと同じ「
2状態2次元外部総和型ムーア近傍ルール」というグループに属するセル・オートマトンで、定義は以下の通りです。
死んだセルに接している生きたセルの個数が3、6、7、8のいずれかであれば、生きたセルに変化する。
生きたセルに接している生きたセルの個数が3、4、6、7、8のいずれかならば、生きたセルのまま変化しない。
Golly(セル・オートマトンのシミュレーションソフト)やLife Wikiなどで使われるルール記法(以下、B/S表記)では、このルールはB3678/S34678と表記されます。
さて、このDay and Nightには非常におもしろい性質が存在します。

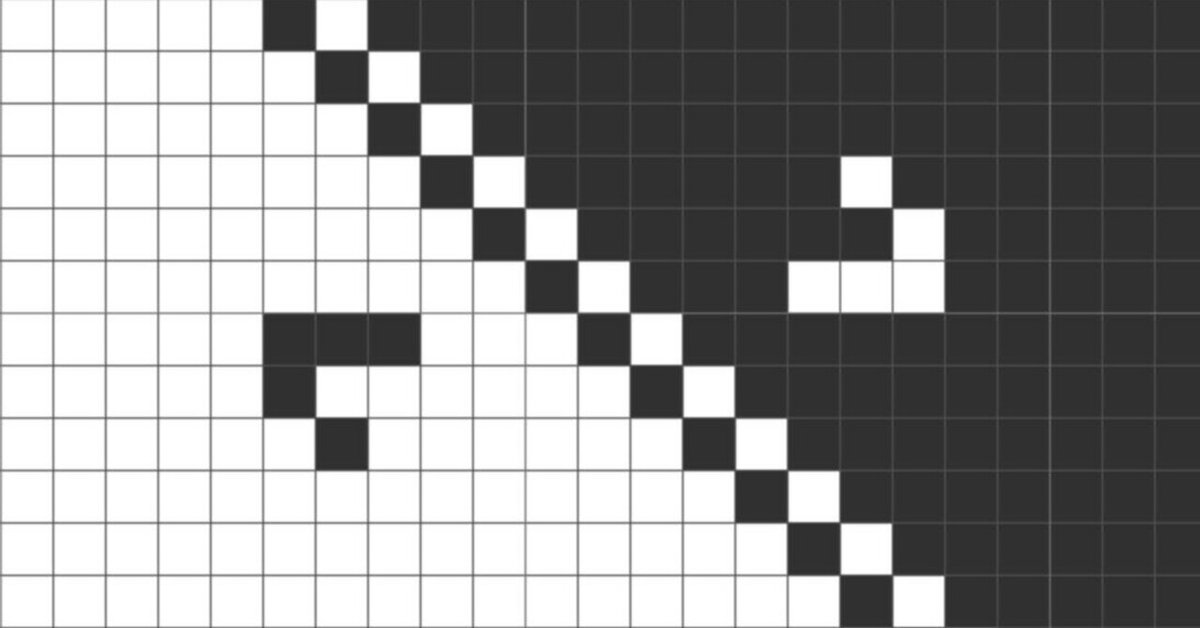
このgif動画の左側では生きたセル(白)が振動物体を形成していますが、右側では生きたセルに囲まれた死んだセル(黒)が全く同じ動きをしています。
実はDay and Nightは、「生きてるセルと死んだセルが等価(入れ替えても同じ挙動になる)」という性質を持っています。
ここまでなら知っているという人もいると思いますが、実はこのような性質を持つセル・オートマトンはDay and Night以外にも存在します。
というわけで、この記事ではDay and Nightのような生死等価セル・オートマトンを探す(作る?)方法を解説します。
外部総和型ルールの場合
セルの状態が数値で表され、あるセルの状態が「そのセルの近傍のセルの状態値の総和」と「そのセル自身の状態」の組み合わせで決まるようなセル・オートマトンのルールを、「外部総和型」(outer totalistic)と呼びます。
例えばライフゲームやDay and Nightの定義は、死んだセルを0番、生きたセルを1番とすると近傍のセルの番号の総和(とセルの状態の組み合わせ)で表せるので外部総和型ルールに含まれます。
そしてルールのB/S表記(ライフゲームはB3/S23、Day and NightはB3678/S34678)は、Bの後の数字が「死んだセルが生きたセルに変化する条件(近傍のセル番号の総和)」、Sの後が「生きたセルが死んだセルに変化しない条件」を表しています。
以上を踏まえて、外部総和型ルールかつ生死等価ルールでもあるようなものを探す方法を考えます。
生きたセルと死んだセルが等価という事は、「死んだセルが生きたセルに変わる条件」と「生きたセルが死んだセルに変わる条件」がある意味で同じ(生と死を入れ替えても変わらない)ということになります。
B/S表記は「死→生」と「生→生」の条件を表すものであり、このままだとややこしいので「『死→生』と『生→死』」を直接表した表記に変換します。
例として、B368/S245というルールを考えます。
このルールのB/S表記を日本語に訳すと以下のようになります。
死んだセルに接している生きたセルの個数が3、6、8のいずれかなら、生きたセルに変化する。
生きたセルに接している生きたセルの個数が2、4、5のいずれかならば、生きたセルのまま変化しない。
2個目のルール(Sの後の数字に対応)を「生→死」の条件に書き換えるとこうなります。
生きたセルに接している生きたセルの個数が0、1、3、6、7、8のいずれかならば、死んだセルに変化する。
さらに、生きたセルの個数ではなく死んだセルの個数を使って書き換えます。
生きたセルに接している死んだセルの個数が8、7、5、2、1、0のいずれかならば、死んだセルに変化する。
1個のセルに接しているセルの個数は常に8個なので、「生きたセルの個数がN」という条件は「死んだセルの個数が8-N」に書き換えられます。
以上の手順により、Sの後ろにあった245という数列は012578(昇順に並べ直してあります)に変換されました。
以下、この手順により「生→死」の条件に書き換えられたルールを「B368/D012578」と表記し、この記法をB/D表記と呼ぶことにします。
さて、Day and NightをB/D表記で表すと「B3678/D3678」になります。
つまり、Day and Nightのルールは以下のように表すことができます。
死んだセルに接している生きたセルの個数が3、6、7、8のいずれかならば、生きたセルに変化する。
生きたセルに接している死んだセルの個数が3、6、7、8のいずれかならば、死んだセルに変化する。
この説明文における「生きたセル」と「死んだセル」という単語を全て入れ替えると、以下のようになります。
生きたセルに接している死んだセルの個数が3、6、7、8のいずれかならば、死んだセルに変化する。
死んだセルに接している生きたセルの個数が3、6、7、8のいずれかならば、生きたセルに変化する。
変換前後のルールを見比べてみると実質的に全く同じルールとなっており、Day and Nightの「生きてるセルと死んだセルが等価」という性質が可視化されたことになります。
そして、この手順を応用することで、以下の手順により生死等価な2状態2次元外部総和型ムーア近傍ルールをつくることができます。
B/D表記でBの後とDの後の数列が等しいルールを作る。
B/D表記からB/S表記に変換する。

ちなみにB25678/S4578はこんな感じのルールです。


等方性非総和型ルールの場合
Gollyでは、外部総和型ルールを拡張した「等方性非総和型」(以下、INT)と呼ばれるルールも扱うことができます。
INTルールの表記法として「Hensel記法」というものがあり、近傍のセル配置に対して以下のように記号を割り振ります。

例えばB34e/S23というルールは、ライフゲームとほぼ同じですが「死んだセルが4つの生きたセルと辺で接している(4e配置)ならば、生きたセルに変化する」というという遷移規則が追加されたルールになっています。
また、数字とアルファベットの間に"-"を入れることで特定の配置を排除することができ、例えばB3-e/S23と書くと「死んだセルが生きたセルと3e配置で接しているときは生きたセルに変化しないが、他はライフゲームと同じ」というルールになります。
さてHensel記法で表せるような等方性非総和型ルールの中で生死等価ルールを探すには、以下の性質が便利です。
性質1:B/S012345678は生死等価ルールである
性質2:ある生死等価ルールに対して、「ある配置を誕生条件に加え、その配置の生きたセルと死んだセルを反転させた配置を生存条件から消す」という操作をしたルールは生死等価ルールである。
まず、一つ目の性質についてはほぼ明らかかと思います。
B/S012345678では、死んだセルは何があっても生きたセルに変化せず、生きたセルも絶対に死んだセルに変化しないので生死等価です。
性質2は少し複雑なので補足します。
まず、「生きたセルと死んだセルを反転させた配置」というのはこういうことです。

生きたセルの個数が4個の場合以外は、「1c↔7c」や「6k↔2k」のように数値を8から引くだけで反転配置が得られるようになっています。
ただし生きたセルが4個の場合だけは不規則で、以下のような関係になっています。

そして、例えば「B/S012345678」→「B3e/S012345-e678」のように誕生条件の追加と生存条件の削除を同時に行うことで新たな生死等価ルールを生成できる、というのが性質2です。
ちなみにこの方法は外部総和型ルールでも利用可能で、「B/S012345678」→「B2/S01234578」みたいな感じで追加&削除の繰り返しで生死等価ルールを作れます。
外部総和型ルールではできなくてもINTルールでなら可能なこととして、「特定の物体が存在する生死等価ルールの作成」というものがあります。(厳密には外部総和型でもできたりINTでもできなかったりすることもありますが、INTルールの方が圧倒的にやりやすいです)
例えば、「グライダーが存在する生死等価ルール」をつくることを考えます。

グライダーの近傍のセルの配置を調べると、以下のようになっています。

生きているセルの近傍配置の内、2e、2a、3n、3j、3rはライフゲームの生存条件(S23)に含まれ、1c、1e、4kは含まれていません。
ということは、生存条件に1c、1e、4kの内のどれか一つでも入っているルールではグライダーは存在できず、2ea3njrの内一つでも欠けているルールでもグライダーは存在できないことになります。
誕生条件でも同様に、12cea4r5nが含まれているルールと3ainjが揃っていないルールはグライダーが存在できません。
以下、「その物体が存在するために絶対にルールに入れておかなければならない配置」を集めたルールをその物体の必須ルール、「その物体が存在するために絶対にルールに入れてはならない配置」を禁止ルールと呼ぶことにします。

グライダーが存在する生死等価ルールを見つけるには、先程説明した手順に従って必須ルールの追加と禁止ルールの削除を行えばOKです。
具体的には、B/012345678に対して
誕生条件に3ainjを追加し、生存条件から5ainjを削除する。
生存条件から14kを削除し、誕生条件に74kを追加する。
という操作を行い、生成されたB3aijn4k7/S0234-k5-aijn678というルールは生死等価ルールであり、なおかつグライダーが存在します。

B3aijn4k7/S0234-k5-aijn678は爆発性が高くてあまり面白くないのですが、必須・禁止ルールに気をつけながら更に条件の追加・削除を行うことで、もう少し面白そうなルールを見つけることができます。
例えばB3aijn4k5aikqy6-ae78/S2ae3cejnr4-k5-aijn678は、グライダー以外にも2種類の小さな移動物体が存在し、棒状の無限増殖物体も見つかっています。

また、B3aijn4k5-ijnr6-ae78/S2ae3ijnr4-k5-aijn678は複数の無限増殖物体が存在し、なおかつほぼ爆発しないルールです。(B3aijn4k5aikqy6-ae78/S2ae3cejnr4-k5-aijn678は非常にゆっくりと爆発していくことがあります)

