ある作図問題とその周辺

どうも、108Hassiumです。

突然ですが、私があるとき熱中した「N点等距離問題」という作図問題とその関連問題を紹介します。

2点等距離問題

まず、全ての始まりとなった2点等距離問題はこんな問題です。

2点等距離問題：長方形$${ABCD}$$の辺上に、$${AP_1=P_1P_2=P_2C}$$が成り立つような2点$${P_1}$$、$${P_2}$$を作図せよ。

便宜上「問題」と書きましたが、正確には作図問題としては不完全です。

まず、長方形の頂点のラベリングの仕方は2種類存在します。

☝2種類の長方形ABC

以下、AとCが辺を共有しているものをシス型、そうでないほうをトランス型とします。(ABCDの配置も上記のものと同じものを使うことにします)

☝シス型とトランス型

さて、シス型とトランス型に分けて考えてもまだ問題としては不完全です。

例えば以下の例のように、同一の長方形に対しても異なる点の配置が存在します。

☝同じトランス型長方形に対する異なる点の配置

私が調べた限りでは、シス型とトランス型を合わせて11種類の点配置が存在するようです。

※以下、作図手順ではなく点の配置のことを「解」と呼ぶことにします。

☝2点等距離問題の11通りの解

さて、問題名に「2点」とあることからわかる通り、この問題には点の個数を変えたバリエーションが存在します。

$${N}$$点等距離問題：長方形$${ABCD}$$の辺上に、$${AP_1=P_1P_2=P_2P_3=…=P_{N-1}P_N=P_NC}$$が成り立つような点$${P_1,P_2P_3,…P_{N-1},P_N}$$を作図せよ。

Nが2以外のときは以下のような解が見つかっています。

☝N=1

☝N=3

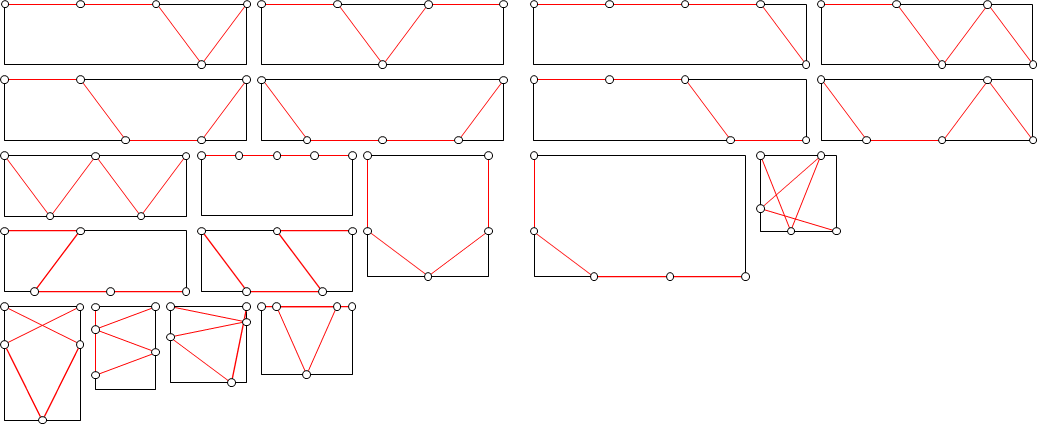
図は省略しますが、N=4では54通りの解が見つかっています。

※長方形の頂点ABCDと点P₁、P₂、P₃・・・の計N+4点のうち一つでも重なるようなものは解としてカウントしないことにします。

こうなると当然「Nの値に対して何通りの解が存在するか」ということが気になってきますが、実はこの問題には問題があります。

今まで特に触れていませんでしたが、何をもって異なる解と見做すかが決まっていないと解を数え上げることはできません。

そして、実は今のところ解を明確に区別する基準は見つけられていません。

疑問1：N点等距離問題の解を区別する基準ってどう定義したらいいの？

先程列挙した解は感覚だけをもとにして何となくで区別していましたが、直感と正確に一致する基準を定めるのは簡単ではなさそうです。

例えば、以下の解を同一の解と見做すのは本当に合理的でしょうか？

どちらの解も、向かい合う辺の3等分点を交互に結ぶという全く同じ方法で構成されたものです。

作図の問題として見れば2点の配置はそれぞれ別物ですが、数え上げ問題の解としては同一視する方が自然に感じます。

また、以下の解はどうでしょうか。

2点等距離問題について考え始めてすぐの時期、私は「どの点がどの辺上にあるか」という情報をもとにして解を識別するコードを考え出しました。

☝識別コードの例(書式は当時のものとは異なる)

※シス型なら1文字目はCisのC

しかし先程の2つの解は点と辺の組み合わせが完全に同一であり、識別コードも同じ「T(BP₂C)(AP₁D)」になります。

悩んだ挙句当時の私は2つのT(BP₂C)(AP₁D)を「同じ長方形で、同じ向きで同時に存在するから」という理由で別物と判定していました。

しかし、後になってからさらにややこしい例が見つかりました。

☝T(AP₃B)(BP₁C)(AP₂D)

どうも、T(AP₃B)(BP₁C)(AP₂D)も同じ長方形で同じ向きで同時に2つ存在するようです。

しかも、T(BP₂C)(AP₁D)が角の大きさで明確に区別できたのと違い、T(AP₃B)(BP₁C)(AP₂D)は特徴が無く別々の解と見做すのには抵抗があります。

・・・というような事情があって、解の列挙を数え上げ問題として厳密に定義することは今のところはできていません。

直観を無視して区別できるものを全て区別していくという選択肢もあるのですが、そうなるとT(AP₃B)(BP₁C)(AP₂D)ペアのようなものを見つけなければならなくなり、数え上げ問題としての難易度が跳ねあがってしまいます。

数え上げ方法が何とかして定義できたとして、解の総数の上限を考えることで以下のような疑問が発生しました。

疑問2-1：$${N}$$点等距離問題の解の個数って$${2×6^N}$$より少ないの？
疑問2-2：$${N}$$点等距離問題の解の個数って$${\frac{(N+3)!}{3}}$$より少ないの？

疑問2-1は点$${P_1,P_2,…P_N,C}$$がどの位置に配置できるかを順番に考えていくことで、疑問2-2は解の識別コードの総パターン数を数えることで導出できる式です。

☝疑問2-1の由来

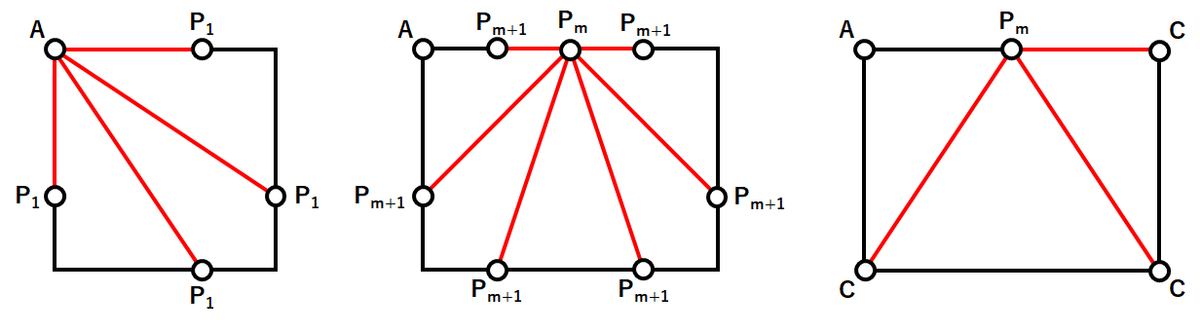
どちらの見積もりでも、実在の解に対応しないパターンも数え上げているため実際の解の個数はもっと小さいだろう、と予想しています。

ただし、どちらもT(AP₃B)(BP₁C)(AP₂D)のような区別しにくい解を無視しており、数え方の定義次第では解の個数の方が上回る可能性もあるため、あくまでも予想として扱います。

さて、基本の話が終わったので、ここからはより細かい性質や派生問題の話をします。

作図可能性

いきなり数え上げ問題の話をしてしまったので忘れた人もいるかもしれませんが、もともとN点等距離問題は作図の問題です。

というわけで、それぞれの解の作図問題としての性質を見ていきましょう。

まず、N=2の各解の作図難易度は以下のようになっています。

☝2点等距離問題の作図難易度

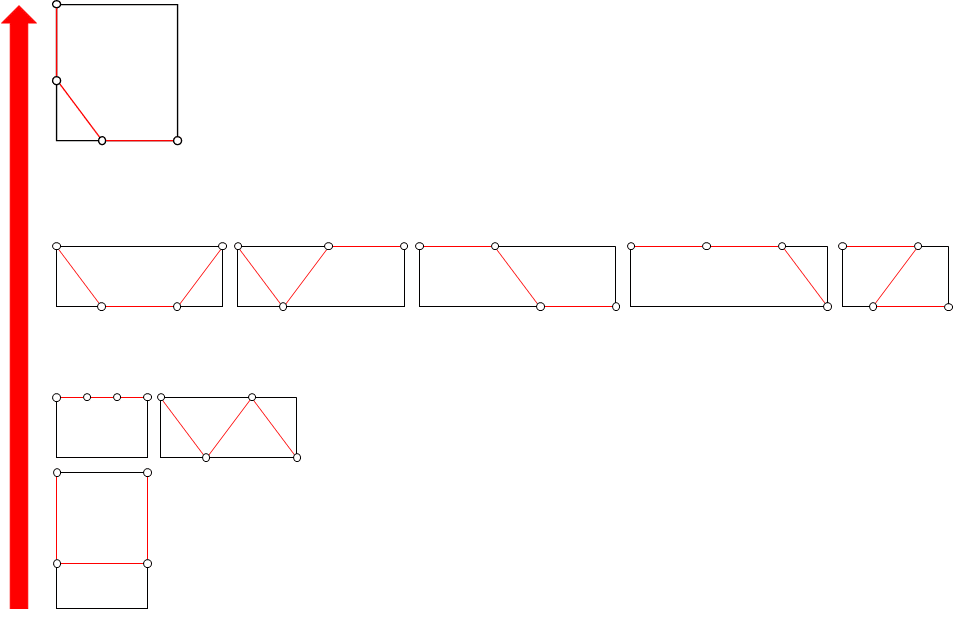
一番下の3つの解については、説明するまでもないと思います。

真ん中の5つの解の内の4つについては、角の二等分線の性質と対称性を利用すると線分の3等分の作図に帰着させられます。

☝AQ:CQ=2:1

C(BP₁D)(AP₂C)はパッと見難しそうですが、点P₁と点Cを通る直線で点P₂を対称移動するとC(BP₁P₂D)の作図に帰着させられることがわかります。

☝C(BP₁D)(AP₂C)からC(BP₁P₂D)への変換

この変換(以下、「菱形変換」)を利用することで作図方法が他の解の作図に帰着できたり、解の数え上げをする際にはある解から他の解を生成することができたりします。

さて、2点等距離問題で作図が一番難しい解であるT(AP₁B)(BP₂C)ですが、菱形反転と角の二等分の組み合わせにより以下のような方法を見つけました。

☝AQ:QC=1:√2

菱形反転により直角二等辺三角形が出現し、それをうまく利用することで1:√2という作図しやすい比が現れます。

この性質をうまく利用することでT(AP₁B)(BP₂C)を作図できるのですが、実は全く別のアプローチによりもっと簡単に作図できます。

まず、線分の長さを以下のように置きます。

そして三平方の定理を使って$${x}$$と$${y}$$の関係を表す方程式を立て、$${y}$$について解きます。

$${(1-y)^2+(x-y)^2=y^2}$$

$${1-2y+y^2+x^2-2xy+y^2=y^2}$$

$${y^2-2(x+1)y+x^2+1=0}$$

$${y=x+1\pm \sqrt{(x+1)^2-(x^2+1)}\\=x+1\pm \sqrt{2x}}$$

先程の図から$${y< x}$$であることがわかるので、ルートの前の符号はマイナスになります。

そして、実はこの$${x+1-\sqrt{2x}}$$という値を直接作図するのが手っ取り早い作図方法になります。

☝菱形反転を使った作図の跡

☝簡単な作図方法の跡

説明は省きますが、最初の図の方が線が多くて複雑なのがわかると思います。

※この記事では作図方法の詳細な説明はしないことにします。

次はN=3ですが、全体的にはN=2より簡単に作図できる解が多いです。

☝簡単に作図できる3点等距離問題の解

上の10個の解は、垂直二等分線の組み合わせだけで簡単に作図できてしまいます。

ただし、一つ一つの解を見ていくとN=2の時のどれよりも難しい解があります。

まずT(AP₃B)(BP₁C)(AP₂D)は、図形的性質に基づいた綺麗な(?)作図方法が見つかっていません。

☝T(AP₃B)(BP₁C)(AP₂D)

辺と平行な線が無いので、どこをどう菱形変換しても作図できそうな感じにならないのです。

ただし、先程のT(AP₁B)(BP₂C)と同じように線分AP₁の長さを直接作図するという方法なら適用可能です。

先程と同様に縦の辺の長さを1、横の辺を$${x}$$、AP₁の長さを$${y}$$とすると$${y}$$は以下のように表せます。

$${y=\sqrt{\frac{11-2x^2\pm\sqrt{21-20x^2}}{8}}}$$

既知の長さと有理数と四則演算・平方根を使って表せる長さは全て作図可能なので、この長さの線分を作図できればT(AP₃B)(BP₁C)(AP₂D)を作図できることになります。

そして、これよりさらに難しいのがC(AP₂B)(BP₃D)(CP₁D)です。

☝C(AP₂B)(BP₃D)(CP₁D)

今までと同じようにAP₁と辺長の方程式を立て、整理すると以下のようになります。

$${256y^8-(896x^2+512)y^6+(1072x^4+256)y^4-(504x^6-688x^4+384x^2)y^2+81x^8-200x^6+144x^4=0}$$

明らかにヤバそうな方程式になりました。

$${y}$$の次数が全て偶数なので$${y^2}$$についての方程式と見做して次数を下げることもできますが、それでも4次です。

一般の3次以上の方程式の解は作図不可能なので、C(AP₂B)(BP₃D)(CP₁D)は作図不可能です。

実際、Wolfram Alpha先生に聞いてみると立方根が混ざった長大な解を出力してくれます。

☝解の内の1つ

なお、方程式自体が複雑で導出過程で計算ミスが発生している可能性が高いので、C(AP₂B)(BP₃D)(CP₁D)が本当に作図不可能解なのかは現時点では未確定であるということにしておきます。

疑問3：N点等距離問題に作図不可能解が存在するNの最小値は？

定数解

2点等距離問題のC(AP₁P₂C)という解には、ちょっとだけ面白い特徴があります。

☝C(AP₁P₂C)

上の図で長方形の縦の辺の長さを$${y}$$、横の辺の長さを$${x}$$としたとき、線分AP₁の長さは$${\frac{1}{3}x}$$となり、$${y}$$に依存しない値になります。

以下、このように「AP₁の長さが長方形の1つの辺の長さにしか依存しない」という性質を満たす解を「定数解」と呼ぶことにします。(「定数」という名前は、横の辺の長さを1とするとAP₁の長さが定数になることに由来しています)

N<3では、以下のような定数解が存在します。

☝N=1～3までの定数解

2点までの定数解はかなり単純なものしか存在しませんが、3点になるとちょっと面白いものが出てきます。

まず右下のC(AP₃P₁B)(CP₂D)は、横の辺の長さを1とするとAP₁の長さが$${\frac{3\sqrt{2}}{4}}$$という少し複雑な値になります。

そしてC(BP₁P₂D)(AP₃C)は、AP₁の長さは縦の辺の長さに依存しないものの、点P₁と点P₂の位置が縦の辺の長さに応じて変化します。

☝C(BP₁P₂D)(AP₃C)の点の配置が縦の辺の長さによって変化する様子

以下、C(BP₁P₂D)(AP₃C)のように点の位置が(縦横両方の)辺の長さに依存するような定数解を「非相似定数解」、そうでない定数解を「相似定数解」と呼ぶことにします。

疑問4：作図不可能な定数解が存在するNの最小値は？

疑問5：作図不可能な非相似定数解が存在するNの最小値は？

疑問6：トランス型の定数解って存在するの？

まず疑問4については、以下のN=7の解が作図不可能っぽいです。

☝C(AP₄P₆P₁B)(CP₅P₂P₇D)(AP₃C)

よって、Nが5か6のときに作図不可能な定数解が存在するかが問題となるかと思います。

一方で疑問5については、作図不可能な非相似定数解の実例すら見つかっていません。

CC(BP₁P₂D)(AP₃C)と同じような発想で見つけられる非相似定数解はAP₁の長さが辺ACの有理数倍にしかならないため、作図不可能な解を見つけるには全く新しい手法が必要になりそうです。

疑問6も同様に、既存の定数解の発見方法はシス型の長方形であることが前提になっているため自力では見つけられていません。

また、定数解と直接は関係していませんが、以下のようなことも気になっています。

疑問7：長方形ABCDの辺の長さを固定してもP₁、P₂、P₃・・・の位置を連続的に動かせるような解って存在するの？

例えばT(AP₃B)(BP₂C)(AP₁D)はすでに述べた通り「同じ長方形において2通りの配置が存在する」という性質を持ちますが、3点等距離問題の条件を満たしたまま一方の配置からもう一方の配置へと連続的に変形することはできません。

しかし、もしかしたらそれが可能な解もあるのではないか、というのが疑問7です。

延長

N点等距離問題の拡張として、以下のようなものを考えました。

延$${N}$$点等距離問題：長方形$${ABCD}$$の辺上またはその延長線上に、$${AP_1=P_1P_2=P_2P_3=…=P_{N-1}P_N=P_NC}$$が成り立つような点$${P_1,P_2P_3,…P_{N-1},P_N}$$を作図せよ。

例えばN=2のとき、以下のような解が存在します。

☝2点等距離問題の解17個

この図はほぼ作図難易度順に並べてあり、右端の3つはおそらく作図不可能です。

なお、問題の定義上はN点等距離問題の解も延N点等距離問題の解に含まれるのですが、この記事では基本的に「延N点等距離問題の解」といったらN点等距離問題の解ではないものを指すことにします。

さて、N点等距離問題に関する疑問の殆どは延N点等距離問題にも適用可能です。

疑問8：延$${N}$$点等距離問題の解の個数って$${\frac{(N+12)!×2}{12!}}$$より少ないの？

疑問2-2の延長版で、解の識別コードを使った評価です。(疑問2-1のような点配置による評価は思いつきませんでした)

識別コードは延N点等距離問題でもほぼ同じように使用することができ、例えば以下の解は「C(P₂BD)(CDP₁)」と表記することができます。

☝C(P₂BD)(CDP₁)

疑問9：延N点等距離問題に作図不可能解が存在するNの最小値は？

前述の通りN=2で作図不可能っぽい解があるので、多分最小値はN=2です。

疑問10：延N点等距離問題に作図不可能な定数解が存在するNの最小値は？

疑問11：延N点等距離問題に作図不可能な非相似定数解が存在するNの最小値は？

疑問12：延N点等距離問題にトランス型の定数解って存在するの？

疑問13：延N点等距離問題に長方形ABCDの辺の長さを固定してもP₁、P₂、P₃…の位置を連続的に動かせるような解って存在するの？

疑問4～7の延長版です。

N点等距離問題で存在したものが延N点等距離問題では存在しない、ということはほとんどなさそうなので疑問12と13の真偽はそれぞれ6、7と一致する気がします。

ちなみにN点等距離問題で非相似定数解が出現したのはN=3でしたが、延N点等距離問題では2点のものがあります。

存在範囲

※これ以降の話も延N点等距離問題に拡張可能ですが、面倒なので今後は延N点等距離問題については極力触れないようにして進めたいと思います。

N点等距離問題の解の中には、その解が存在するような長方形の縦横比が制限されているものがあります。

例えばC(AP₁B)(CP₂D)は、縦の辺に対して横の辺が長いと点P₁と点P₂が長方形の辺の外にはみ出してしまいます。

☝C(AP₁B)(CP₂D)の点の配置が横の辺の長さによって変化する様子

ここで、縦の辺の長さを1、横の辺の長さを$${x}$$とし、特定の解の存在範囲を$${x}$$についての不等式で表すことにします。

なお、長方形の頂点ABCDとP₁、P₂、P₃・・・の計N+4点のうち一つでも重なるような場合は存在範囲に含めないことにします。

例えば先程のC(AP₁B)(CP₂D)の場合、$${x=1}$$のときはP₁とP₂がB、Dと重なり、それより長い場合はP₁とP₂が変の外にはみ出すため、存在範囲は「$${x<1}$$」となります。

さて、T(BP₂C)(AP₁D)の存在範囲はちょっと特殊です。

☝T(BP₂C)(AP₁D)の点の配置が横の辺の長さによって変化する様子

前述の通りT(BP₂C)(AP₁D)は同じ長方形で同じ向きで同時に2種類存在するのですが、$${x}$$を短くしていくと$${x=\sqrt{3}}$$のときに2つの解が重なり同一の解になります。($${x<\sqrt{3}}$$のときはどちらの解も存在できなくなります)

同一の解の中で点の重なりが起きるわけではないので$${x=\sqrt{3}}$$のケースを存在範囲に含めるとすると、T(BP₂C)(AP₁D)の存在範囲は$${\sqrt{3}\leq x}$$になります。

なおこの記事の最初の方で「2つのT(BP₂C)(AP₁D)は角の大きさで明確に区別できる」と書きましたが、あれは嘘です。

上のgif動画を見ればわかる通り、$${\sqrt{3}< x<2}$$のときはどちらの解でも角AP₁P₂が鋭角になります。

存在範囲に関しては、以下のような疑問が未解決です。

疑問14：存在範囲が閉区間になる解って存在するの？

閉区間とは、$${a\leq x\leq b}$$という形の区間です。

これに近いものとしてはT(AP₃B)(BP₁C)(AP₂D)の$${1< x\leq\frac{\sqrt{39}}{6}}$$という結果がありますが、両側が等号付き不等号になるものは見つかっていません。

疑問15：存在範囲の幅が0の解って存在するの？

$${x}$$が特定の値ピッタリのときのみ存在するような解は無いのか、ということです。

ちなみに$${x=a}$$という条件は$${a\leq x\leq a}$$と同値なので、この問題が肯定的に解決されれば疑問14も解けたことになります。

疑問16：存在範囲の上限か下限に作図不可能数が現れる解が存在するNの最小値は？

作図不可能数とは、四則演算と平方根の有限回の組み合わせで表せない数のことです。

実は存在範囲はAP₁の長さなどと違って確実に求める方法がわかっていない(そもそも定義が曖昧ですが)のですが、大抵代数方程式で求められるので作図不可能数になることもあるだろう、と予想しています。

また、N=4の解の存在範囲はまだあまり調べていないのですが、複雑すぎて計算できそうにない解が存在するのでNの最小値は4だろうと思っています。

☝存在範囲が不明な解の一つ、T(AP₄B)(BP₁C)(CP₂D)(AP₃D)

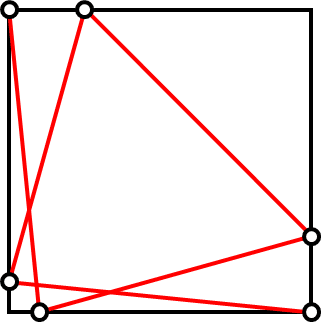
疑問17：「N点等距離問題の解の存在範囲の幅(0を除く)の最小値の逆数」の増加速度はどのくらい？

存在範囲の定義のほか、解の判別方法にも依存する曖昧さのある問題です。

とりあえず区別できるものをなるべく全部区別し、「$${N}$$点等距離問題(略)の最小値の逆数」の値を$${f(N)}$$とすると、現在見つかっている解による$${f(N)}$$の下限は以下のようになっています。

• $${f(1)\geq1}$$(T(BP₁C))

• $${f(2)\geq2}$$(T(BP₁P₂C))

• $${f(3)\geq13+2\sqrt{39}\approx 25.49}$$(T(AP₃B)(BP₁C)(CP₂D))

☝f(1)～f(3)の下限に対応する解とその存在範囲

サンプル図

解の具体例を表す図(以下、サンプル図)を描くとき、格子点をうまく使うと描きやすくなります。

☝格子を使ったサンプル図の作図

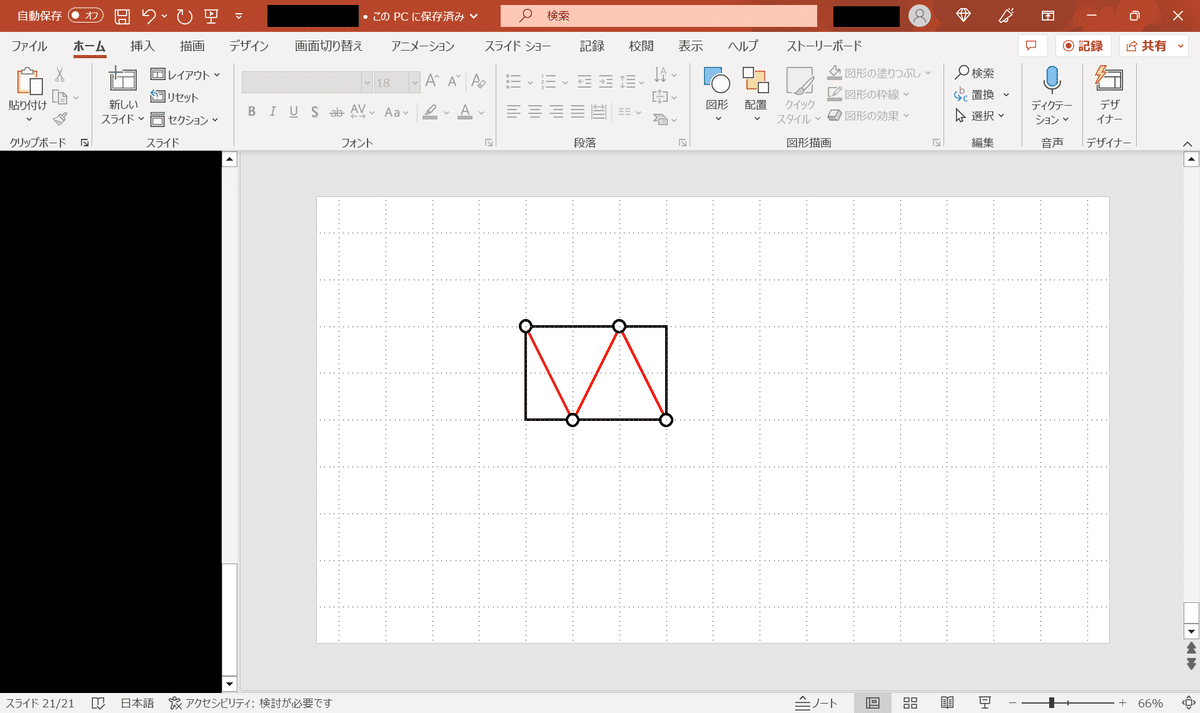
例えばT(BP₁C)(AP₂D)のサンプル図を作成する場合、横の辺の長さが3の倍数になるように長方形を描くことで簡単かつ正確に図を描くことができます。

また、C(BP₁P₂D)のような辺と平行な線と斜めの線が混ざった解でも、3:4:5のピタゴラス三角形をうまく使うことでサンプル図が得られることがあります。

☝C(BP₁P₂D)と格子

しかし複雑な形状の解だと上手くいかず、例えばT(AP₃B)(BP₁C)(AP₂D)なんかは3点が全て格子点に乗るような組み合わせが見つかっていません。

☝この記事で使用されているT(AP₃B)(BP₁C)(AP₂D)のサンプル図は、
実は目分量で描いた近似図です

かつて私がN点等距離問題にハマっていたころ、ドット入りのルーズリーフに研究結果(?)をまとめてファイリングしたりしていたので、格子点に乗るサンプル図について考えるようになるのはほぼ必然的でした。

というわけで、まずは以下の用語を定義します。

座標整数解：N点等距離問題の解の具体例の内、点A、B、C、D、P₁、P₂、P₃・・・の座標を全て整数にできるもの。
距離整数解：N点等距離問題の解の具体例の内、長方形ABCDの全ての辺の長さとAP₁の長さを整数にできるもの。
完全整数解：N点等距離問題の解の具体例の内、座標整数解と距離整数解の両方に該当するもの。

整数「解」という単語を使っていますが、定数解とは異なり1種類ずつの解のさらに具体的なA、B、C、D、P₁、P₂、P₃・・・の組み合わせを指す単語です。

例えば定数解は「C(AP₁C)は定数解だが、C(BP₁D)は定数解ではない」というような使い方のできる単語ですが、整数解は「C(BP₁D)はAC=6、AB=4のとき座標定数解かつ距離定数解になるのでC(BP₁D)は完全整数解をもつ」というように使います。

少々トリッキーな完全整数解を持つ解として、C(BP₂D)(AP₃P₁C)というものがあります。

☝C(BP₂D)(AP₃P₁C)の完全整数解(AB=12,AC=16,AP₁=13)

この整数解は5:12:13のピタゴラス三角形から構成されたものですが、3:4:5のピタゴラス三角形で同じことをしようとすると点P₁と点P₃が長方形の外にはみ出してしまいます。

C(AP₃P₁B)(CP₂D)は、座標整数解も距離整数解も持たない解の一つです。

☝C(AP₃P₁B)(CP₂D)

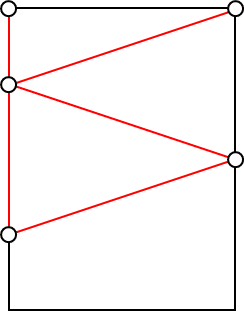
AP₁の長さは辺ACの$${\frac{3\sqrt{2}}{4}}$$(無理数)倍なので距離整数解にはなり得ず、同様の理由により座標整数解にもならないことがわかります。

座標整数解と距離整数解が存在するのかどうかすらわかっていない解としては、C(AP₂B)(BP₃D)(CP₁D)とT(AP₃B)(BP₁C)(AP₂D)があります。

☝C(AP₂B)(BP₃D)(CP₁D)とT(AP₃B)(BP₁C)(AP₂D)

ちなみにT(AP₃B)(BP₁C)(AP₂D)の方に関しては、点の重なりを許すならAB=BC=2のときに2つの解が両方とも座標整数解になり、その内の片方が距離整数解にもなります。

☝T(AP₃B)(BP₁C)(AP₂D)の整数解もどき

座標整数解が見つかっているものの距離整数解が見つかっていないものとして、C(AP₃B)(BP₂D)(CP₁D)とT(AP₄B)(BP₁C)(CP₃D)(AP₂D)があります。

☝C(AP₃B)(BP₂D)(CP₁D)とT(AP₄B)(BP₁C)(CP₃D)(AP₂D)

逆に座標整数解の方が見つかっていない解としては、C(AP₃B)(BP₁P₄D)(CP₂D)があります。

☝C(AP₃B)(BP₁P₄D)(CP₂D)

この解はAP₁=ACになる非相似定数解で、ACとABが整数であれば距離整数解になるのは明らかですが、座標整数解にもなるような組み合わせは見つかっていません。

延2点等距離問題では、「座標整数解も距離整数解も見つかっているが、完全整数解は見つかっていない」という状態の解があります。

☝C(P₂BD)(CDP₁)の座標整数解と距離定数解

整数解に関する疑問は、個別の解に関するものを挙げていくとキリがないので一般的な話のみ紹介します。

疑問18：座標整数解はあるけど距離整数解はない解って存在するの？

疑問19：距離整数解はあるけど座標整数解は無い解って存在するの？

疑問20：座標整数解も距離整数解もあるのに完全整数解は無い解って存在するの？

先程紹介した数々の例に関するものです。

ただし、作図不可能性の話題と違って既に挙げたものが具体例になっているという確証はかなり弱いです。

また、C(P₂BD)(CDP₁)はあくまでも延N点等距離問題の解であり、疑問18の具体例の候補は今のところ一つも見つかっていません。

疑問21：作図不可能かつ完全整数解を持つ解って存在するの？

「座標整数解が見つかっているが距離整数解が見つかっていない解」の例として紹介したT(AP₄B)(BP₁C)(CP₃D)(AP₂D)は、実は作図不可能解っぽいです。

疑問22：距離整数解を持たない非相似定数解って存在するの？

C(AP₃B)(BP₁P₄D)(CP₂D)は「座標整数解を持たない非相似定数解」ですが、それの逆バージョン(?)の問題です。

疑問5で言及した「作図不可能な非相似定数解」が存在すればこの問題も解決されるので、整数解に関する問題の中では比較的簡単そうな気がします。

整数解に関する大抵の問題は連立ディオファントス方程式に帰着されるので、何となくほかの問題より難しそうな印象を持っています。

整数解とは関係ないですが、サンプル図に関してこんな疑問があります。

疑問23：作図可能なサンプル図を持たない解って存在するの？

例えばC(AP₂B)(BP₃D)(CP₁D)は作図不可能解(の候補)ですが、サンプル図は作図可能です。

C(AP₂B)(BP₃D)(CP₁D)

辺ACの長さと点P₁の位置を決めるとP₂とP₃の位置が決まり、P₃の位置が決まることで辺ABの長さも決まってサンプル図が完成します。

☝同様な手法でサンプル図が作図可能な、4点等距離問題の作図不可能解

以下の2つの解は、少し事情が異なります。

☝T(AP₄B)(BP₁C)(CP₃D)(AP₂D)とT(AP₄B)(BP₂C)(CP₁D)(AP₃D)

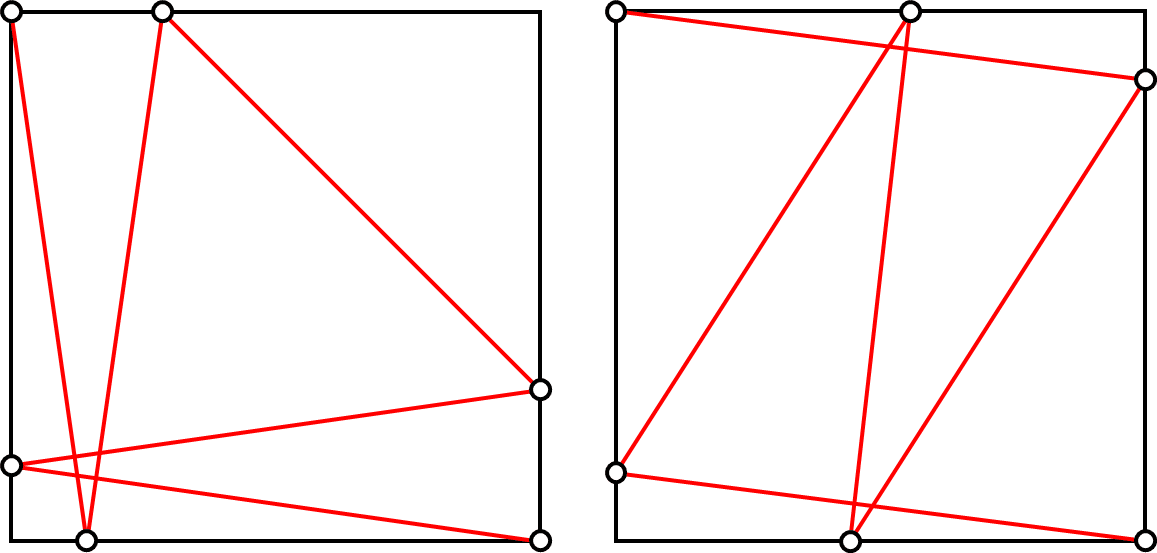
どちらの解も「長方形の形以外を先に決めて、4点の位置を決めてから長方形を描く」という手法による作図方法は見つかっていないのですが、作図可能なサンプル図の具体例は見つかっています。

T(AP₄B)(BP₁C)(CP₃D)(AP₂D)は既に紹介したとおり座標整数解が存在し、T(AP₄B)(BP₂C)(CP₁D)(AP₃D)の方は整数解ではないもののAB=BC=1のときに各点の座標が作図可能数になることを確認しています。

そして、T(AP₄B)(BP₁C)(CP₂D)(AP₃D)は現時点で作図可能なサンプル図の具体例すら見つかっていない「最強の作図不可能解」です。

☝T(AP₄B)(BP₁C)(CP₂D)(AP₃D)

なおサンプル図の作図はN点等距離問題の通常の作図問題とは異なり、ほぼ何の制限もない初期状態から作図を始めることができてしまうため、特定の解が作図可能なサンプル図を持たないことを証明するのは通常の作図不可能性の証明よりもかなり難しいのではないかと思います。

ただし、「作図不可能な相似定数解」が存在すれば作図可能なサンプル図を持たない解にもなっているはずなので、疑問23の解決自体はそんなに難しくないのかもしれません。

最後に

紹介したい内容はもう少しあるのですが、疑問の数が計23問というキリのいい数字になったのでこの辺で終わりたいと思います。

それではさようなら。

おまけ1

記事内で提示した疑問のリストです。

疑問1：N点等距離問題の解を区別する基準ってどう定義したらいいの？
疑問2-1：$${N}$$点等距離問題の解の個数って$${2×6^N}$$より少ないの？
疑問2-2：$${N}$$点等距離問題の解の個数って$${\frac{(N+3)!}{3}}$$より少ないの？
疑問3：N点等距離問題に作図不可能解が存在するNの最小値は？
疑問4：作図不可能な定数解が存在するNの最小値は？
疑問5：作図不可能な非相似定数解が存在するNの最小値は？
疑問6：トランス型の定数解って存在するの？
疑問7：長方形ABCDの辺の長さを固定してもP₁、P₂、P₃・・・の位置を連続的に動かせるような解って存在するの？
疑問8：延$${N}$$点等距離問題の解の個数って$${\frac{(N+12)!×2}{12!}}$$より少ないの？
疑問9：延N点等距離問題に作図不可能解が存在するNの最小値は？
疑問10：延N点等距離問題に作図不可能な定数解が存在するNの最小値は？
疑問11：延N点等距離問題に作図不可能な非相似定数解が存在するNの最小値は？
疑問12：延N点等距離問題にトランス型の定数解って存在するの？
疑問13：延N点等距離問題に長方形ABCDの辺の長さを固定してもP₁、P₂、P₃・・・の位置を連続的に動かせるような解って存在するの？
疑問14：存在範囲が閉区間になる解って存在するの？
疑問15：存在範囲の幅が0の解って存在するの？
疑問16：存在範囲の上限か下限に作図不可能数が現れる解が存在するNの最小値は？
疑問17：「N点等距離問題の解の存在範囲の幅(0を除く)の最小値の逆数」の増加速度はどのくらい？
疑問18：座標整数解はあるけど距離整数解はない解って存在するの？
疑問19：距離整数解はあるけど座標整数解は無い解って存在するの？
疑問20：座標整数解も距離整数解もあるのに完全整数解は無い解って存在するの？
疑問21：作図不可能かつ完全整数解を持つ解って存在するの？
疑問22：距離整数解を持たない非相似定数解って存在するの？
疑問23：作図可能なサンプル図を持たない解って存在するの？

おまけ2

疑問24：Note始めてからちょうど30本目の記事がこんな内容でいいのか？