
今週のフラクタル10 (z^2+ixy+c)
どうも、108Hassiumです。
今週は$${z^2+ixy+c}$$($${x}$$と$${y}$$は$${z}$$の実部と虚部)に関するフラクタル図形を紹介します。
「今週のフラクタル」シリーズも今回で10回目ですが、今後も特に変わらずやっていきたいと思います。
z^2+ixy+c
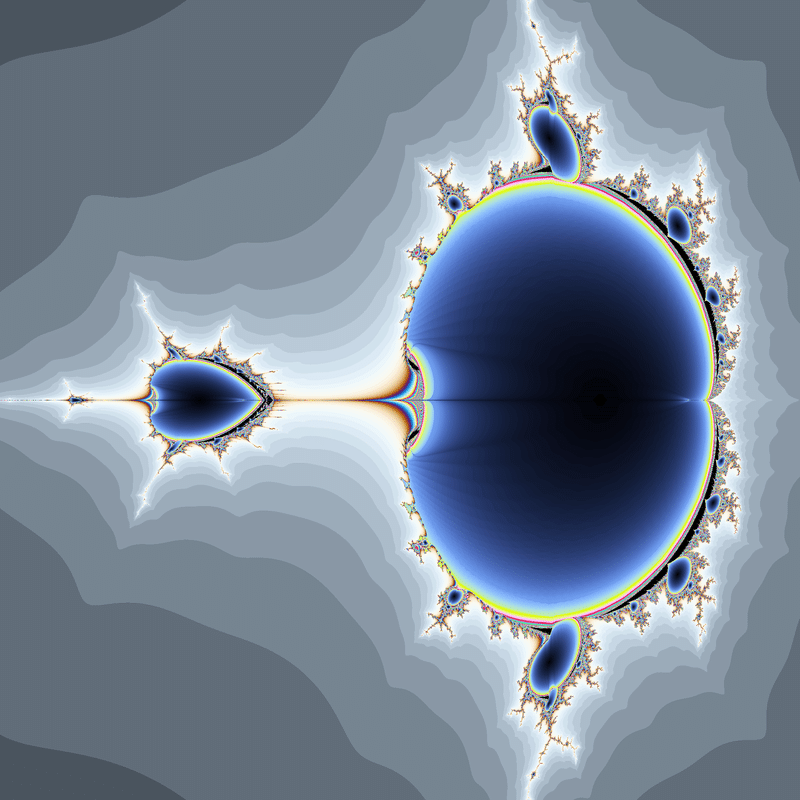
大まかなシルエットは$${z^2+c}$$に似ていますが、左側の領域がちぎれ飛んでいることや所々に真っ黒い領域($${z_n}$$が周期数列に収束しない領域)が見られることなどが特徴的です。

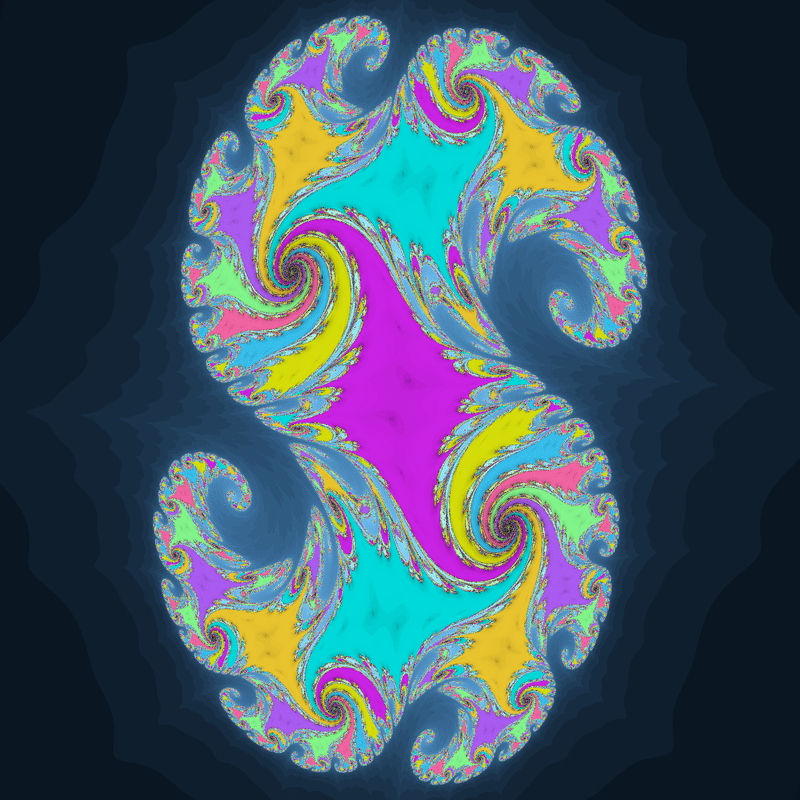

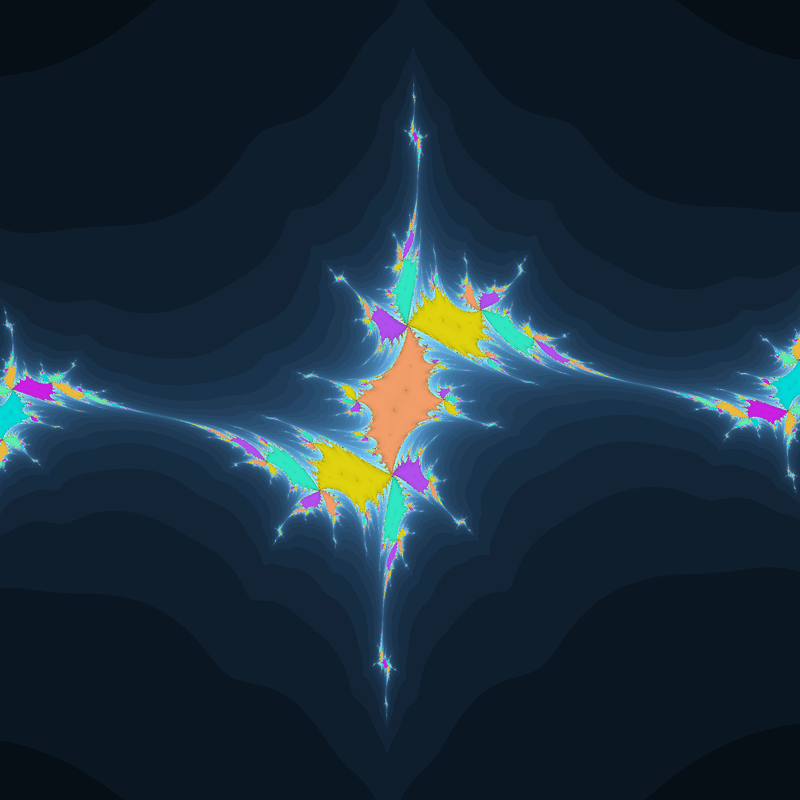
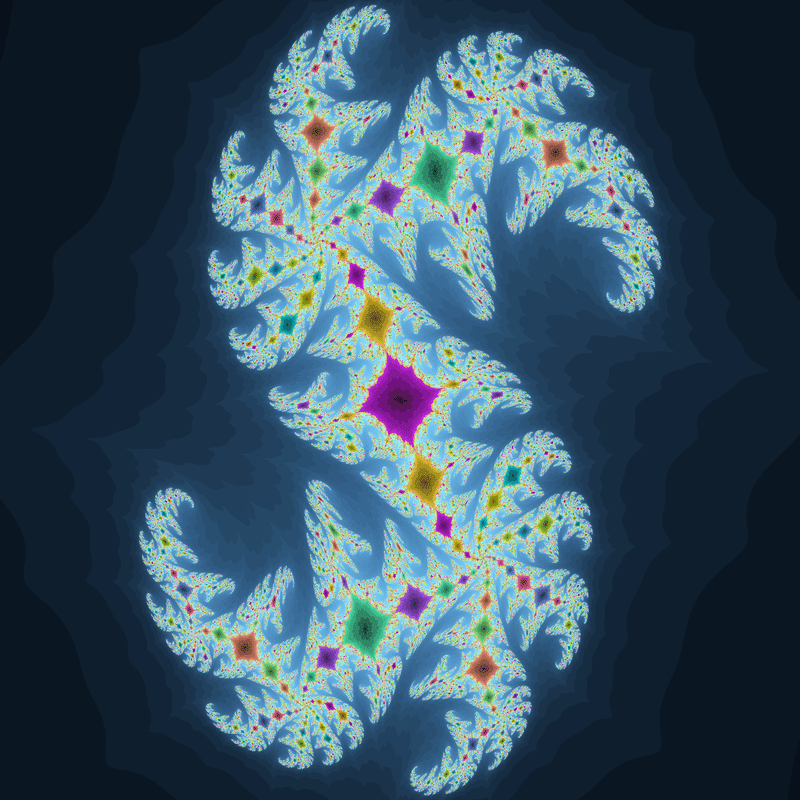
ジュリア集合の形状も、$${z^2+c}$$のものと同様に凹凸や枝分かれ、渦巻きなどが見られますが、よく見ると潰れたり引き延ばされたような形をしている部分があります。



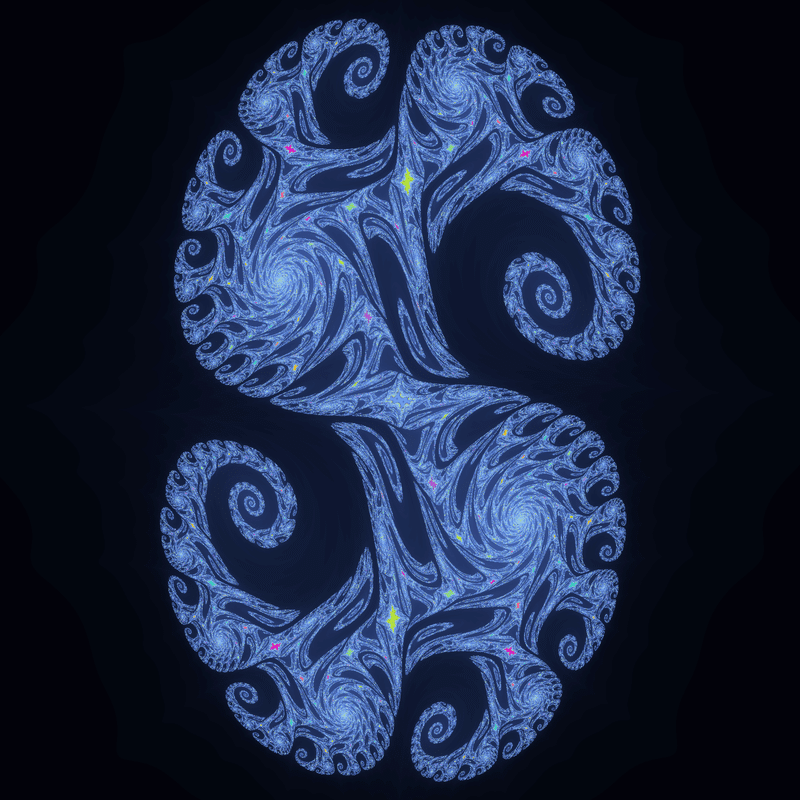
発散領域の線状の模様も、$${z^2+c}$$のものと似てるようで違う感じになります。




私が普段載せている画像は収束領域の陰影がなるべく滑らかになるようにパラーメータを調節して描画しているのですが、今回は渦巻き状や花状の面白い模様が現れたものがあったのでそれを活かしてみました。
ちなみに最後の$${z^2+ixy+0.03+0.53i}$$のものは収束領域の形自体がかなり変な形になっていますが、同じような見た目のものは見つからなかったのでなぜこんな形になるのかは謎です。
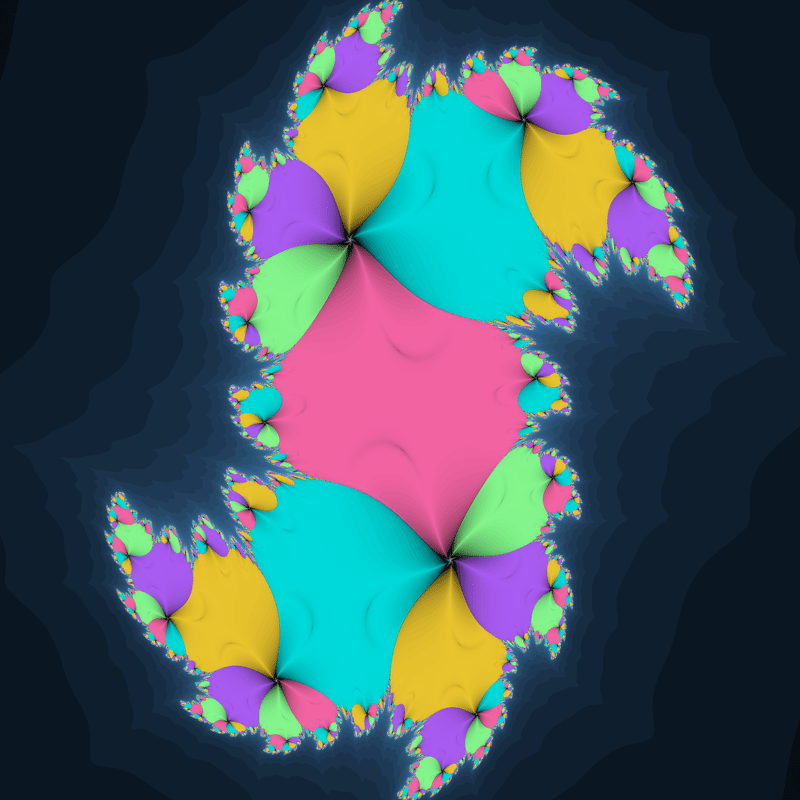




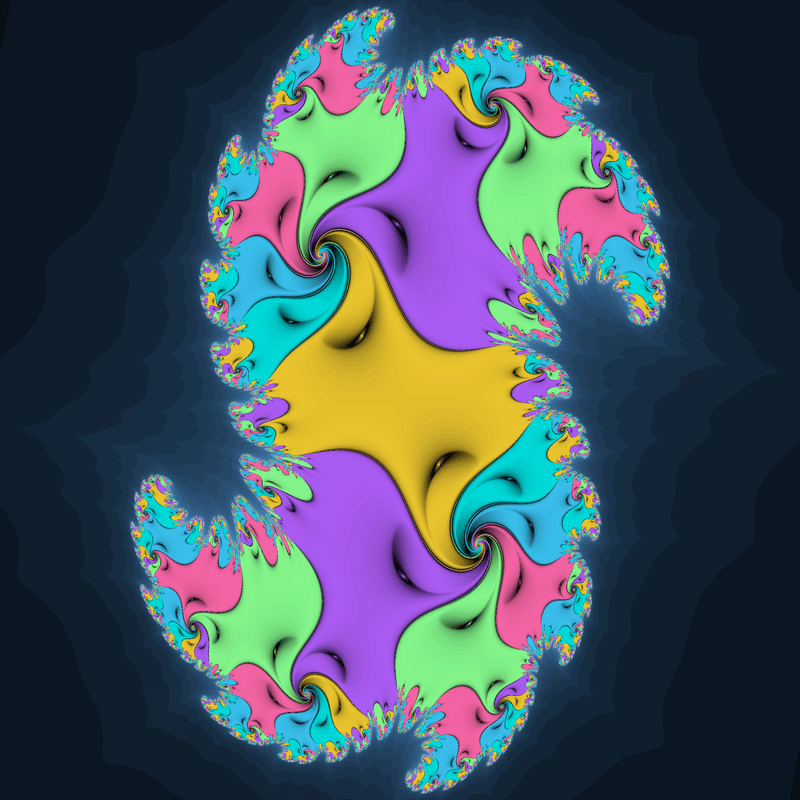

枝分かれした収束領域がぴったりくっついたような形のジュリア集合です。
このようなジュリア集合は解析的関数だと$${\frac{z^3}{z+0.1i}+c}$$や$${\frac{2z^3}{z^2+4iz+0.27}+c}$$のような分数関数によく見られますが、非解析的関数ならこのような単純な関数でも見られるようです。



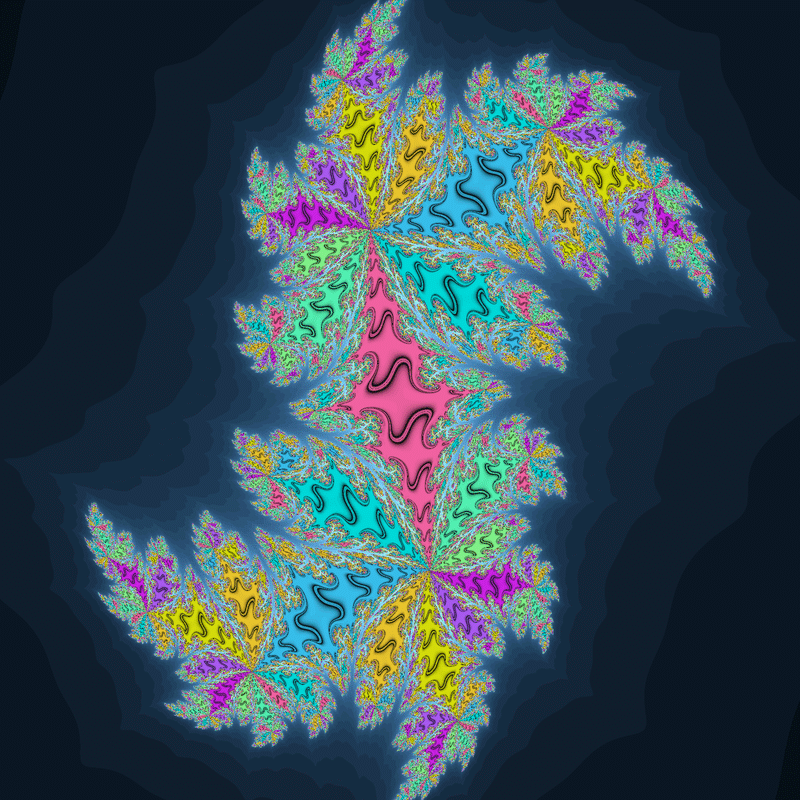

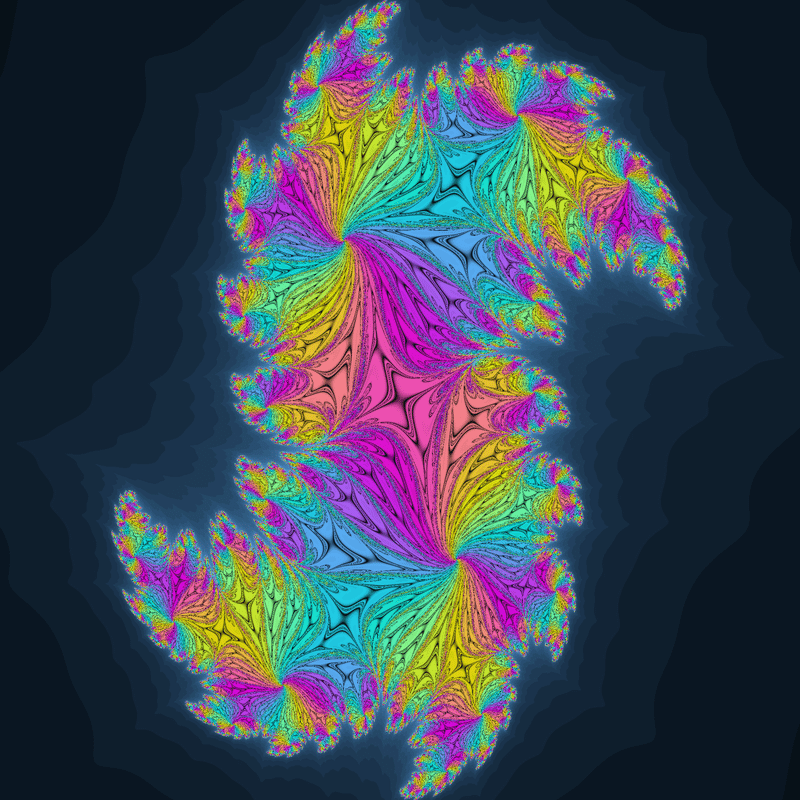
収束領域に割れ目のような線があるジュリア集合です。
この線は先ほどの「収束領域がくっついたようなジュリア集合」の領域の境目とは違うらしく、彩色関数のパラメータを弄ってもこの線に沿って色が分かれることは無いようです。







$${z_0=0}$$から到達できるサイクルとは違うサイクルが存在するジュリア集合です。
既に紹介した「収束領域がくっついたようなジュリア集合」もそうですが、何故か摂動ジュリア集合に似た性質が時折見られるようです。





いつものです。

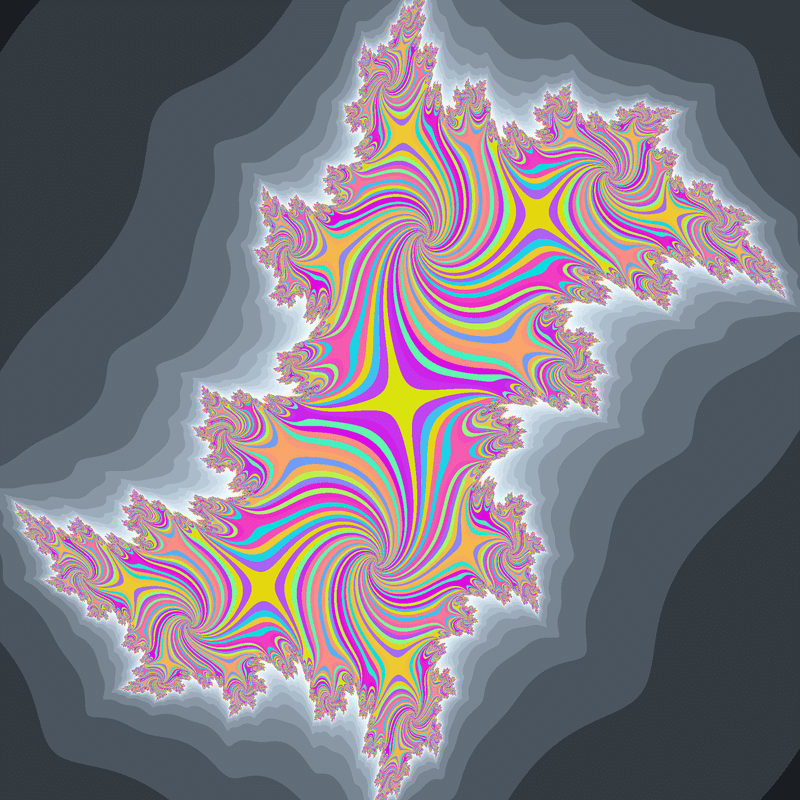


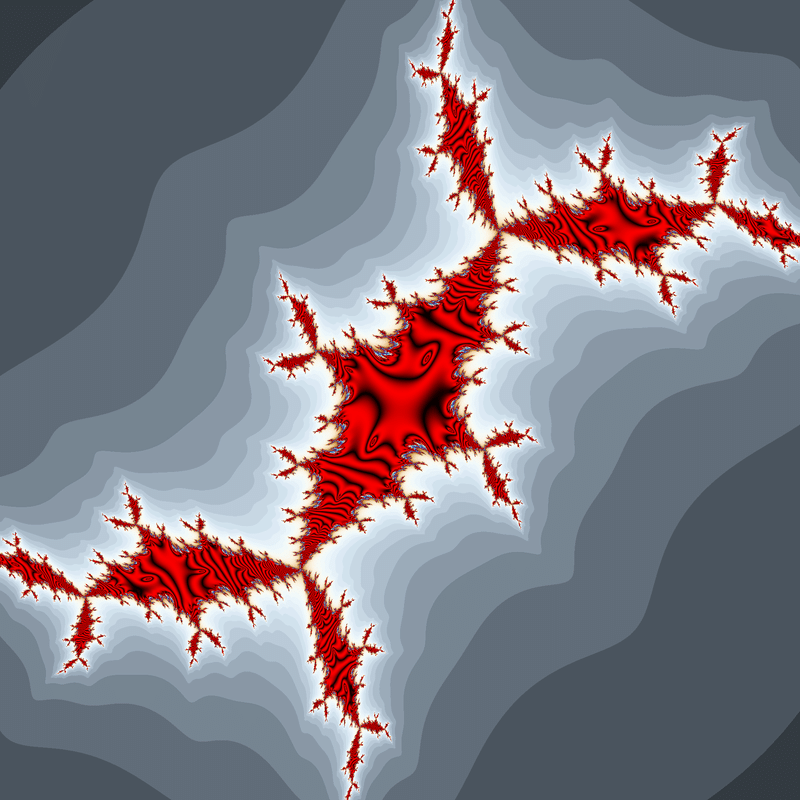


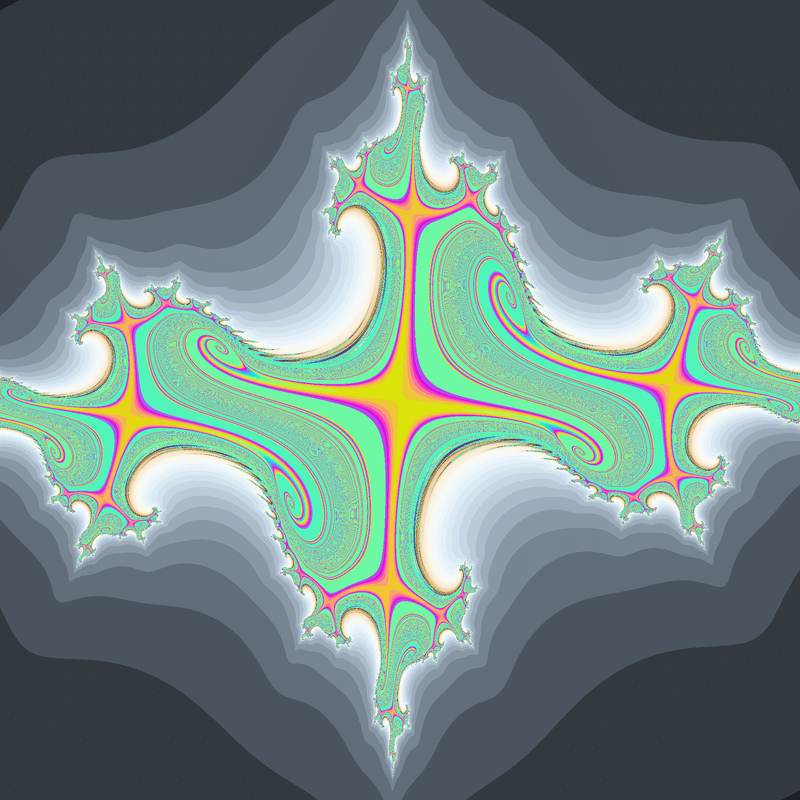
無限周期ジュリア集合です。
解析的関数では非常に限られた条件でしか無限周期のジュリア集合は生成されませんが、非解析的関数なら簡単に見つかります。
※☟解析的関数の無限周期ジュリア集合に関する記事


ごくわずかですが、無限周期ジュリア集合の中にはストレンジアトラクターを生成するものもありました。
ちなみにこのジュリア集合を無限周期ジュリア集合用の彩色方法で彩色すると、グッチャグチャのモザイク状の模様になってしまいます。
一般化
$${z^2+irxy+c}$$のマンデルブロ集合(r=-5~1)を描画してみました。

どうやら黒い領域が存在しなくなるのは、r=-4($${\text{con}(z)^2+c}$$)とr=0($${z^2+c}$$)のときだけっぽいです。
