
今週のフラクタル18 (c/(z^3-1)+1)
どうも、108Hassiumです。
今週は$${\frac{c}{z^3-1}+1}$$に関するフラクタル図形をお届けします。
c/(z^3-1)+1

$${\frac{c}{z^3-1}+1}$$という関数は、1→∞→1というサイクルを持つ2周期発散関数です。
$${\frac{c}{z^n-1}+1}$$は「臨界点は$${z=0}$$のみで、多重度は$${n-1}$$」「ジュリア集合は$${n}$$回回転対称」という性質を持ち、2周期発散関数におけるマルチブロのような存在です。



細部を拡大すると、$${z^3+c}$$のジュリア集合に似た形が現れることがあります。

これは$${\frac{c}{z^3-1}+1}$$に限った話ではないですが、マンデルブロ集合を拡大した際に現れるジュリア集合っぽい形の中をさらに拡大してみると、ジュリア集合を大きく変形させたりくっつけたりしたような図形が見つかることがあります。



前述の通り、ジュリア集合は3回回転対称になります。


このジュリア集合はよく見ると収束領域と穴の形が同じになっている部分があり、収束領域と穴が同じ色になるように彩色すると6回回転対称っぽくなります。

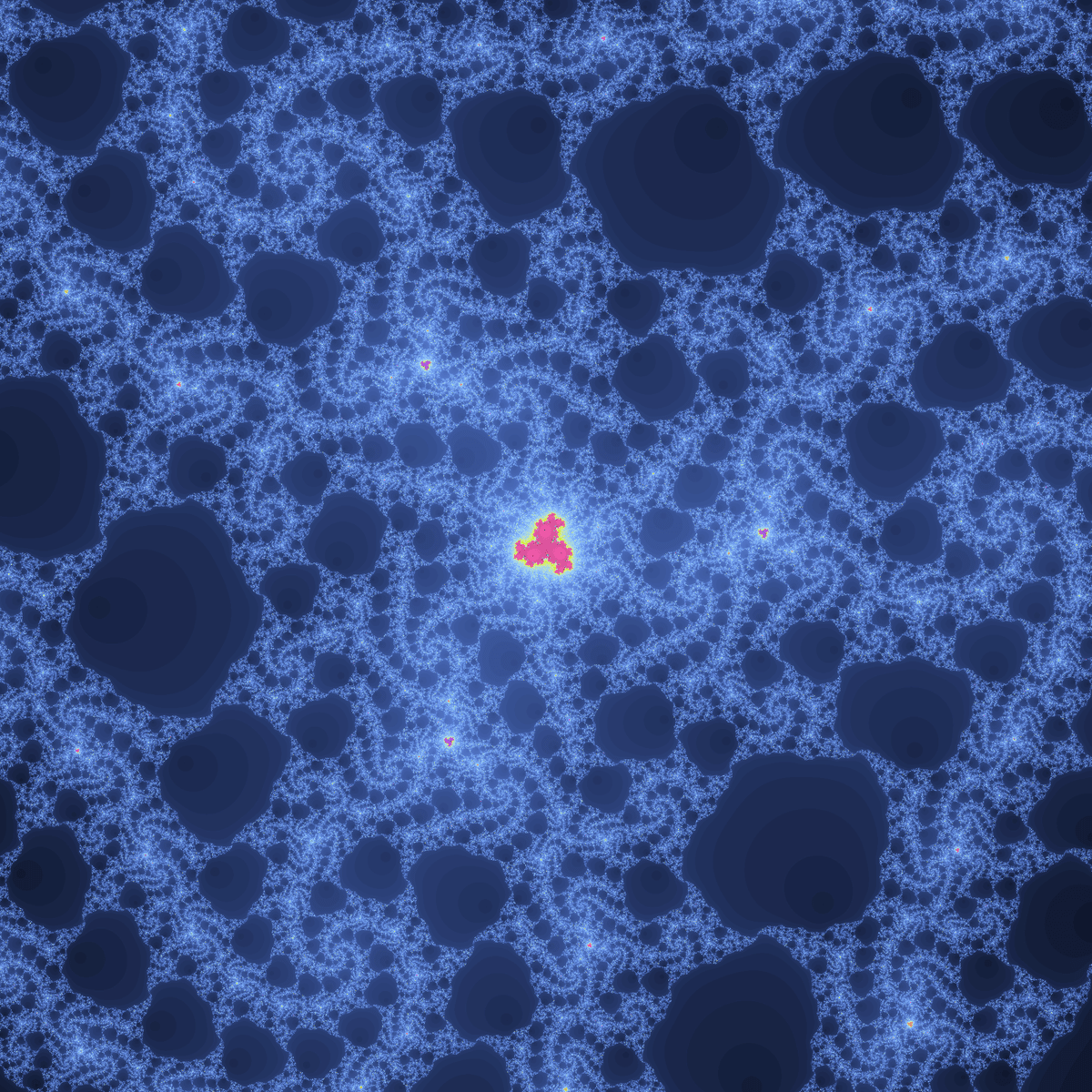

網目模様が美しい飛び地型ジュリア集合です。






いつものやつです。

無限周期と思しきジュリア集合です。
以前の記事で「無限周期ジュリア集合にも通常のものとは異なる周期の概念がある」「3周期以上の無限周期ジュリア集合は見たことが無い」と書きましたが、このジュリア集合が本当に無限周期ならなんと8周期になります。
z+(z^3-1+c)(z^3-1)/(3cz^2)

$${\frac{c}{z^3-1}+1}$$のニュートンフラクタルのマンデルブロ集合です。
※☟ニュートンフラクタルの説明
次数が0以下の有理関数の場合、ニュートンフラクタルには発散領域が生じることがあるようです。




$${z^3+c}$$のジュリア集合とニュートンフラクタルがどちらも3回回転対称になるのと同じように、$${\frac{c}{z^3-1}+1}$$のニュートンフラクタルも3回回転対称になるようです。

$${\frac{2}{z^3-1}+1}$$のジュリア集合と同じく、これだけ6回回転対称になっています。(関連性は不明です)

$${\frac{c}{z^3-1}+1=0}$$の解は$${c=1}$$のときだけ1個になるので、このような見た目になります。



$${\frac{c}{z^3-1}+1=0}$$の解に収束しない領域が出現することもあるのですが、収束先のサイクルは1個の場合(0.88+0.04iと0.5+0.18i)と3個に分かれる場合(0.4+1.1i)の2パターンがあるようです。
