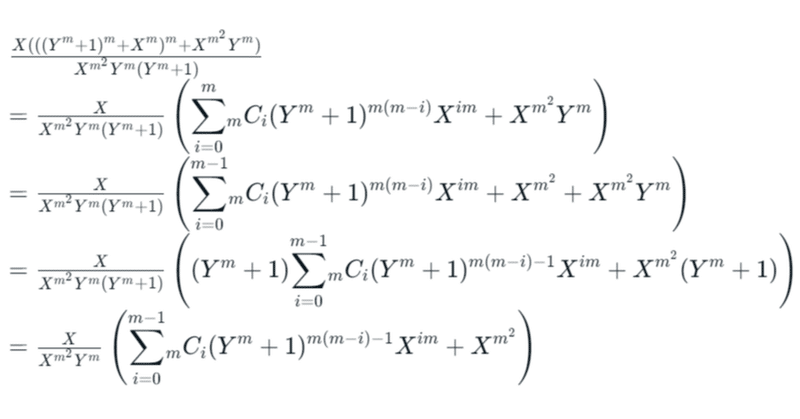
【2】何だこの数列?
どうも、108Hassiumです。
以前、こんな記事を書きました。
この記事で扱った内容に関して、新たな情報がいくつか得られたのでそれを紹介します。
ローラン多項式
前回の記事では、おまけとして以下の数列を紹介しました。
$${\begin{cases}b_0=b_1=1\\b_{n+2}=\frac{b_{n+1}^3+1}{b_n}\end{cases}}$$
$${b_n=1,1,2,9,365,5403014,432130991537958813…}$$
この数列はOEISに載っているのですが、そのページを機械翻訳に掛けて読んでみると少し気になる情報が書かれていました。


「ローラン多項式」でググると、以下のwikipediaの記事がヒットしました。
どうやらローラン多項式は、多項式の指数を負の整数に拡張したもの、もしくは単項式を分母とする有理関数だそうです。
そして、OEISの記述は「$${b_n}$$は$${b_0}$$と$${b_1}$$を変数とするローラン多項式として表せる」という意味っぽいです。
$${b_0=b_1=1}$$なので、$${b_n}$$が$${b_0}$$と$${b_1}$$の(整数係数の)ローラン多項式で表せるならば$${b_n}$$が整数になることの証明に使えそうです。
また、$${a_n}$$の方にも同じ性質があれば、前回微妙にスッキリしなかった「なぜ割り切れるのか」という疑問に対して前回の証明とは別の見方を与えることができそうです。
ということで、まずは$${a_n}$$の最初の方の項を計算してローラン多項式になっているかどうかを確認してみます。
$${a_0=x}$$
$${a_1=y}$$
$${a_2=\frac{y^2+1}{x}}$$
$${a_3=\frac{a_2^2+1}{a_1}=((\frac{y^2+1}{x})^2+1)\frac{1}{y}=\frac{(y^2+1)^2+x^2}{x^2y}}$$
$${a_4=\frac{a_3^2+1}{a_2}=((\frac{(y^2+1)^2+x^2}{x^2y})^2+1)\frac{x}{y^2+1}=\frac{(y^2+1)^4+2x^2(y^2+1)^2+x^4+x^4y^2}{x^3y^2(y^2+1)}=\frac{(y^2+1)^3+2x^2(y^2+1)+x^4}{x^3y^2}}$$
式の長さがとんでもないことになりそうなので、この辺でやめておきます。
$${a_3}$$まではローラン多項式になって当然なのですが、$${a_4}$$では分母に出てきた$${y^2+1}$$が約分により消えています。
この約分が発生したことに関しては理由や背景の類は見つけられず、$${a_5}$$以降がローラン多項式になることを直感的に理解することはできませんでした。
なお、ローラン多項式になること自体は前回発見した線形漸化式を用いれば証明可能です。
$${a_0}$$と$${a_1}$$は、明らかに$${a_0}$$と$${a_1}$$を変数とするローラン多項式である。
$${a_{n+2}=\frac{a_0^2+a_1^2+1}{a_0a_1}a_{n+1}-a_n}$$が成り立つ。
ローラン多項式の和と積はローラン多項式なので、$${a_k}$$と$${a_{k+1}}$$がローラン多項式ならば$${a_{k+2}}$$もローラン多項式である。
数学的帰納法により、全ての非負整数$${n}$$について$${a_n}$$は$${a_0}$$と$${a_1}$$を変数とするローラン多項式として表せる。
結局のところ、$${a_n}$$が整数になる理由について「$${a_n}$$は$${a_0}$$と$${a_1}$$を変数とするローラン多項式として表せるから」と答えると、「じゃあなんでローラン多項式になるの?」という疑問が発生するのであまりいい答えにはならなさそうです。
次は$${b_n}$$の方を確認してみます。
$${b_0=x}$$
$${b_1=y}$$
$${b_2=\frac{y^3+1}{x}}$$
$${b_3=((\frac{y^3+1}{x})^3+1)\frac{1}{y}=\frac{(y^3+1)^3+x^3}{x^3y}}$$
$${b_4=((\frac{(y^3+1)^3+x^3}{x^3y})^3+1)\frac{x}{y^3+1}=\frac{((y^3+1)^3+x^3)^3+x^9y^3}{x^8y^3(y^3+1)}=\frac{(y^3+1)^9+3x^3(y^3+1)^6+3x^6(y^3+1)^3+x^9+x^9y^3}{x^8y^3(y^3+1)}=\frac{(y^3+1)^8+3x^3(y^3+1)^5+3x^6(y^3+1)^2+x^9}{x^8y^3}}$$
自力で計算してみるとわかりやすいのですが、式の形や約分の発生の仕方が$${a_n}$$と非常によく似ています。
しかし、$${b_n}$$の場合は$${a_n}$$の線形漸化式のような都合のいい関係式が見つかっていないため、ローラン多項式であることの証明は難しそうです。
突然の解決
何とかして$${b_n}$$が$${b_0,b_1}$$のローラン多項式であることを証明できないか試行錯誤していたところ、ローラン多項式とほとんど関係ない方法で$${b_n}$$が整数になることを証明できてしまいました。
まず、冒頭で説明したとおり$${b_0,b_1,b_2,b_3}$$は全て整数です。
次に、$${b_k,b_{k+1},b_{k+2},b_{k+3}}$$が全て整数であると仮定します。
このとき、$${b_k=X,b_{k+1}=Y}$$とすると$${b_{k+2}}$$と$${b_{k+3}}$$は以下のように表せます。
$${b_{k+2}=\frac{Y^3+1}{X}}$$
$${b_{k+3}=((\frac{Y^3+1}{X})^3+1)\frac{1}{Y}=\frac{(Y^3+1)^3+X^3}{X^3Y}}$$
そして、$${b_{k+4}}$$は以下のように変形できます。

以上より、$${b_k,b_{k+1},b_{k+2},b_{k+3}}$$が全て整数であれば$${b_{k+4}}$$も整数であることがわかります。
よって、数学的帰納法により全ての非負整数$${n}$$について$${b_n}$$は整数になります。
途中の式変形が複雑そうに見えますが、実は$${a_n}$$と$${b_n}$$を一般化した以下の数列に対してもほとんど同じ方法が使えます。
$${\begin{cases}A_0(m)=A_1(m)=1\\A_{n+2}(m)=\frac{A_{n+1}(m)^m+1}{A_n(m)}\end{cases}}$$
まず、$${A_k(m)=X}$$、$${A_{k+1}(m)=Y}$$と置いて$${A_{k+2}(m)}$$と$${A_{k+3}(m)}$$を計算します。
$${A_{k+2}(m)=\frac{Y^m+1}{X}}$$
$${A_{k+3}(m)=\left(\left(\frac{Y^m+1}{X}\right)^m+1\right)\frac{1}{Y}=\frac{(Y^m+1)^m+X^m}{X^mY}}$$
これを使って$${A_{k+4}(m)}$$を変形し、整数係数多項式による関係式の導出を目指します。
まず、$${A_{k+4}(m)}$$を定義通りに計算します。
$${A_{k+4}(m)=\left(\left(\frac{(Y^m+1)^m+X^m}{X^mY}\right)^m+1\right)\frac{X}{Y^m+1}=\frac{X(((Y^m+1)^m+X^m)^m+X^{m^2}Y^m)}{X^{m^2}Y^m(Y^m+1)}}$$
分母の$${Y^m+1}$$が邪魔なので、分子を少し展開して約分で消します。(分子の$${X}$$も約分で消せますが、後で使うのであえて残します)

次に、右端にある$${X^{m^2}}$$を消すために$${((Y^m+1)^m+X^m)^m}$$を無理矢理作ります。

右の総和の方の$${Y^m+1}$$を1個だけ括り出して整理します。

これで整数係数多項式による関係式が導出できました。
あとは細部を補ったり整えたりすれば、$${A_n(m)}$$が整数になることの証明が得られます。
さらに、以下の数列に対しても応用可能です。
$${\begin{cases}c_0=c_1=c_2=1\\c_{n+3}=\frac{c_{n+2}c_{n+1}+1}{c_n}\end{cases}}$$
説明は省略しますが、$${A_n(m)}$$と似たような感じの式変形により$${c_{n+6}=c_{n+5}c_{n+4}c_n-c_{n+4}^2c_{n+1}-c_{n+2}}$$という関係式が得られます。
試してないので分かりませんが、もしかすると前回名前だけ出した「ソモスの数列」も整数係数多項式による関係式が存在するのかもしれませんね。
おまけ
おまけです。
似たような数列
$${\begin{cases}B_0(m)=B_1(m)=B_2(m)…=B_m(m)=1\\B_{n+m+1}(m)=\frac{B_{n+1}(m)B_{n+2}(m)B_{n+3}(m)…B_{n+m}(m)+1}{B_n(m)}\end{cases}}$$
$${B_n(2)=c_n}$$で、$${B_n(3)}$$はA051786、$${B_n(4)}$$はA072713としてOEISに載っていました。
$${\begin{cases}P=p_1,p_2,p_3,…p_m\\C_0(P)=C_1(P)=C_2(P)…=C_m(P)=1\\C_{n+m+1}(P)=\frac{C_{n+1}(P)^{p_1}C_{n+2}(P)^{p_2}C_{n+3}(P)^{p_3}…C_{n+m}(P)^{p_m}+1}{C_n(P)}\end{cases}}$$
$${C_n(m)=A_n(m)}$$で、$${p_1=p_2=p_3…=p_m=1}$$のときが$${B_n(m)}$$に対応しています。
なお、$${C_n(0,2)=1,1,1,2,5,26,\frac{677}{2}…}$$のように整数にならない数列も混ざっています。
ソースコード
noteの仕様のせいで画像で代用する羽目になった数式のデータを置いておきます。
$${b_{k+4}=\left(\left(\frac{(Y^3+1)^3+X^3}{X^3Y}\right)^3+1\right)\frac{X}{Y^3+1}\\=\frac{X((Y^3+1)^8+3X^3(Y^3+1)^5+3X^6(Y^3+1)^2+X^9)}{X^9Y^3}\\=\frac{X((Y^3+1)^9+3X^3(Y^3+1)^6+3X^6(Y^3+1)+X^9-((Y^3+1)^9+3X^3(Y^3+1)^6+3X^6(Y^3+1)^3)+(Y^3+1)^8+3X^3(Y^3+1)^5+3X^6(Y^3+1)^2)}{X^9Y^3}\\=\frac{X((Y^3+1)^3+X^3)^3}{X^9Y^3}-\frac{X((Y^3+1)^9+3X^3(Y^3+1)^6+3X^6(Y^3+1)^3-(Y^3+1)^8-3X^3(Y^3+1)^5-3X^6(Y^3+1)^2)}{X^9Y^3}\\=Xb_{k+3}^3-\frac{X((Y^3+1)^9+3X^3(Y^3+1)^6+3X^6(Y^3+1)^3-(Y^3+1)^8-3X^3(Y^3+1)^5-3X^6(Y^3+1)^2)}{X^9Y^3}\\=b_{k+3}^3b_k-\frac{Y^3(Y^3+1)^8+3X^3Y^3(Y^3+1)^5+3X^6Y^3(Y^3+1)^2+(Y^3+1)^8+3X^3(Y^3+1)^5+3X^6(Y^3+1)^2-(Y^3+1)^8-3X^3(Y^3+1)^5-3X^6(Y^3+1)^2}{X^8Y^3}\\=b_{k+3}^3b_k-\frac{Y^3(Y^3+1)^8+3X^3Y^3(Y^3+1)^5+3X^6Y^3(Y^3+1)^2}{X^8Y^3}\\=b_{k+3}^3b_k-\frac{(Y^3+1)^8}{X^8}-\frac{3(Y^3+1)^5}{X^5}-\frac{3(Y^3+1)^2}{X^2}\\=b_{k+3}^3b_k-b_{k+2}^8-3b_{k+2}^5-3b_{k+2}^2}$$$${\frac{X(((Y^m+1)^m+X^m)^m+X^{m^2}Y^m)}{X^{m^2}Y^m(Y^m+1)}\\=\frac{X}{X^{m^2}Y^m(Y^m+1)}\left(\displaystyle{\sum_{i=0}^m}{}_mC_i(Y^m+1)^{m(m-i)}X^{im}+X^{m^2}Y^m\right)\\=\frac{X}{X^{m^2}Y^m(Y^m+1)}\left(\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)}X^{im}+X^{m^2}+X^{m^2}Y^m\right)\\=\frac{X}{X^{m^2}Y^m(Y^m+1)}\left((Y^m+1)\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)-1}X^{im}+X^{m^2}(Y^m+1)\right)\\=\frac{X}{X^{m^2}Y^m}\left(\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)-1}X^{im}+X^{m^2}\right)}$$$${\frac{X}{X^{m^2}Y^m}\left(\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)-1}X^{im}+X^{m^2}\right)\\=\frac{X}{X^{m^2}Y^m}\left(\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)-1}X^{im}-\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)}X^{im}+\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)}X^{im}+X^{m^2}\right)\\=\frac{X}{X^{m^2}Y^m}\left(\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)-1}X^{im}-\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)}X^{im}+((Y^m+1)^m+X^m)^m\right)\\=\frac{X((Y^m+1)^m+X^m)^m}{X^{m^2}Y^m}+\frac{X}{X^{m^2}Y^m}\left(\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)-1}X^{im}-\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)}X^{im}\right)\\=A_{k+3}(m)^mA_k(m)+\frac{X}{X^{m^2}Y^m}\left(\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)-1}X^{im}-\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)}X^{im}\right)}$$$${A_{k+3}(m)^mA_k(m)+\frac{X}{X^{m^2}Y^m}\left(\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)-1}X^{im}-\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)}X^{im}\right)\\=A_{k+3}(m)^mA_k(m)+\frac{X}{X^{m^2}Y^m}\left(\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)-1}X^{im}-(Y^m+1)\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)-1}X^{im}\right)\\=A_{k+3}(m)^mA_k(m)-\frac{XY^m}{X^{m^2}Y^m}\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i(Y^m+1)^{m(m-i)-1}X^{im}\\=A_{k+3}(m)^mA_k(m)-\displaystyle{\sum_{i=0}^{m-1}}{}_mC_i\frac{(Y^m+1)^{m^2-im-1}}{X^{m^2-im-1}}\\=A_{k+3}(m)^mA_k(m)-\displaystyle{\sum_{i=0}^{m-1}}{}_mC_iA_{k+2}(m)^{m^2-im-1}}$$