
日本国内の新型コロナワクチンの接種者数と超過死亡率の因果関係について(2021年1月3日~2022年8月28日)
1. はじめに
ご無沙汰しております,zukeiです.これまで国単位で,新型コロナワクチンの接種回数と新型コロナ死亡者数や超過死亡との関係を,因果探索と呼ばれる統計的な手法で探ってきました.
今回は,日本全国のワクチン接種回数と超過死亡の関係を,時系列的な因果探索の手法で探っていきたいと思います.結論を先に言うと,65才以上の新型コロナワクチンのブースター接種は,超過死亡に対して先行関係を示すGranger因果を有し,推定で1万人以上の新型コロナワクチン接種由来の死者を発生させている可能性があります.
2. データ
2.1 超過死亡者数と新型コロナ死亡者数
超過死亡者数のデータは,超過死亡ダッシュボードの全死因(Estimates_weighted.csv)を使いました.このデータは週単位の集計値であり,データの取得時期は期末で,期間は2017年1月1日~2022年8月28日です.加えて新型コロナ死亡者数のデータを,厚生労働省のサイトから「死亡者数(累積)」をダウンロードし,週単位で集計しなおしました.
図1にこの期間の,理論死亡者数($${Japan\_Estimated}$$),実績死亡者数($${Japan\_Observed}$$),新型コロナ死亡者数($${death\_covid}$$)の時系列データを示します.理論死亡者数は,過去のデータから高齢化や季節要因などを加味して調整した平均的な死亡者数です.この数値と実測値の差が超過(過少)死亡者数となります.

ただこの死亡者数には前述したトレンドや周期性があり,後述する回帰モデルでは扱いにくいため,これらの影響を除去した以下の超過死亡率を定義します.ここでtはデータの期(週)を表します.
$$
超過死亡率(t)=\frac{実測死亡者数(t)}{理論死亡者数(t)} (1)
$$
式(1)を数式で書くと以下となります.
$$
omr(t)=\frac{Japan\_Observed(t)}{Japan\_Estimated(t)} (2)
$$
さらに,超過死亡率を計算する際に,新型コロナ死亡者数を減じた超過死亡率を次式で定義します.
$$
omr\_nc(t)=\frac{Japan\_Observed(t)-death\_covid(t)}{Japan\_Estimated(t)} (3)
$$
図2は図1に対応する超過死亡率です.超過死亡率が1ということは,その期で超過死亡が発生していないことを示し,その値が大きくなるほど超過死亡の度合いが大きくなることを意味します.青が全死亡者の超過死亡,オレンジが新型コロナ死亡者数を除いた超過死亡です.当然青のほうが大きくなりますが,新型コロナ流行後はオレンジのほうも依然として超過死亡が目立ちます.

もう少しわかりやすく把握するために,新型コロナ流行前(201701_202203),新型コロナ流行開始後(202003_202104),新型コロナワクチン接種開始後(202104_202208)の3期に分け,それぞれの超過死亡率の分布を図示したものを,図3,4に示します.またこれらの分布の基礎統計を表1に示します.超過死亡率はおおよそ[0.95, 1.05]の範囲に収まるのが通常なので,平均値は1.0近辺の値に収まります.しかし,ワクチン接種開始後は平均値が大きく上昇しています.よく超過死亡の原因は,新型コロナによる死亡であるといわれたりしますが,その数を除いた$${omr\_nc}$$でも,依然として新型コロナ流行前よりも統計的に高い水準に超過死亡率がとどまっているのがわかります.実際これらの期間の分布の差を多重比較で検定すると,有意水準0.001で有意差が出ます.そこで以降では,新型コロナ死を除いた超過死亡である$${omr\_nc}$$を説明する要因を探っていきます.



2.2 その他のデータ
2.2.1 新型コロナ陽性者数
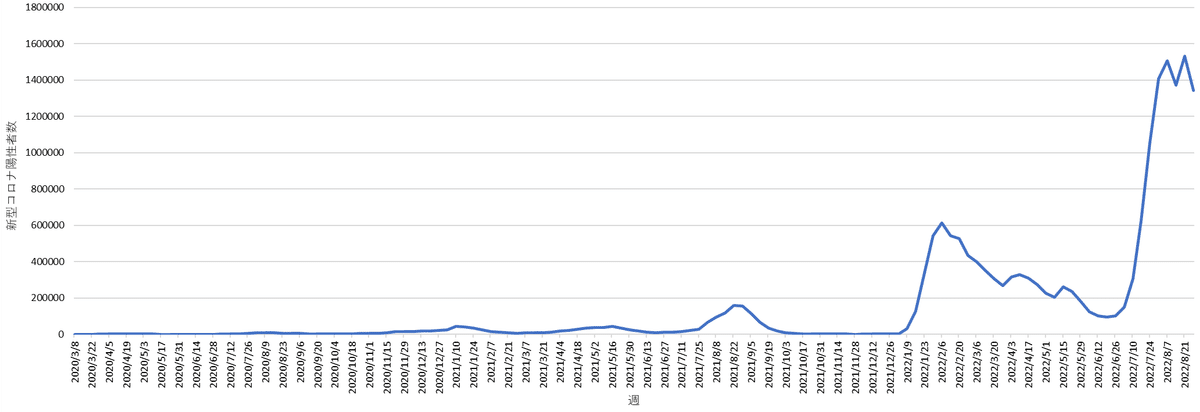
同じく厚生労働省のサイトから,「新規陽性者数の推移(日別)」をダウンロードし,週ごとに集計しました(図5)
2.2.2 新型コロナワクチン接種者数
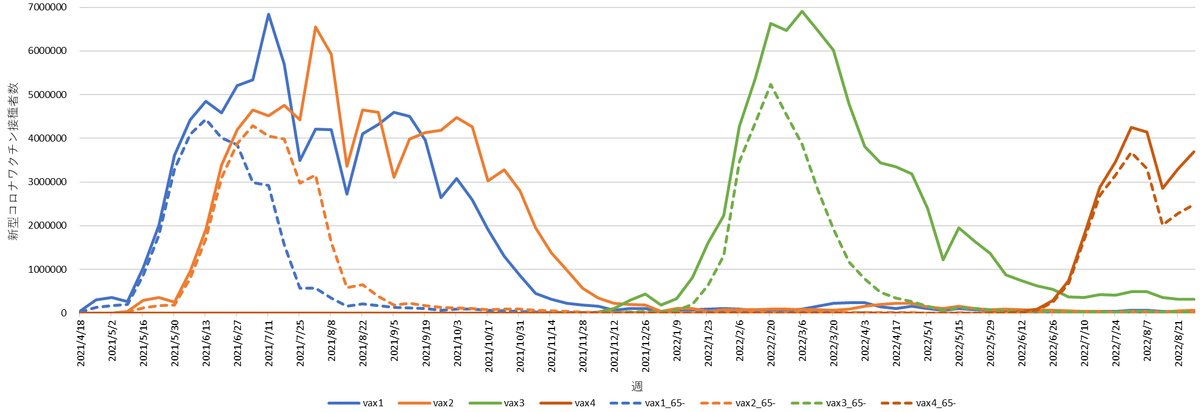
デジタル庁のVRSのサイトから,「都道府県別接種回数詳細(NDJSON)」をダウンロードしました.このデータは接種回数毎の一日単位での各都道府県単位での接種者の集計値ですが,接種者の年齢を64歳以下と65歳以上で区別する項目があります.死亡者の大多数が高齢者であることから,新型コロナワクチンの接種者数も年齢で区別することには意味があると考え,全年齢と65歳以上の2種類の接種者数のデータを用いることにしました.全国の週単位で集計したデータを図6に示します.
2.2.3 救急搬送困難件数
あるサイトで,救急搬送困難事案が超過死亡者数をよく説明するとあったので,総務省消防庁のサイトから「各消防本部からの救急搬送困難事案に係る状況調査の結果(データベース)エクセルファイル」をダウンロードして,週単位で集計しました(図7).

3.時系列データの因果探索
今回は前回までと異なり時系列データを扱うので,因果探索手法の中でも多変量の時系列データを扱えるVARLiNGAMを使用します.この方法に関する解説は,例えばこのリンクが詳しいです(ちなみにzukeiはこれらの方と全く面識はありません).
3.1 入力データ
用いるデータは,先に示した新型コロナ死亡者を除いた超過死亡率($${osm\_nc}$$),新型コロナ陽性者数($${case}$$),救急搬送困難事例数($${emg}$$),そして全年齢と65歳以上のワクチン接種者数です.ここで,ワクチン接種者数は,前回の世界の超過死亡率の検証結果で,デルタ株までとオミクロン株以降でワクチン効果が反転していることから,既定の2回目まで($${vax12|var12\_65}$$)と3・4回目のブースター接種($${vax34|var34\_65}$$)を,区別して集計することにしました.
ワクチン接種が本格的に始まるのは2021年4月18日を期末とする週ですが,VARLiGAMの入力データがある程度過去のデータを必要とするため,入力するデータの期間を2021年1月3日から2022年8月28日としました.さらにVARLiGAMに入力する各データは,計算を適切に行うため,期間内で平均0,標準偏差1になるよう標準化しています.
図8,9に,新型コロナワクチンの接種者の年齢別の標準化した時系列データを示します.


なお,時系列データをVARLiNGAMのような自己回帰モデルで分析する場合,各時系列データが「見せかけの回帰」を有しないことを保証するために,単位根検定と呼ばれる検定を行う必要があります.表2は「各時系列データが単位根である」という帰無仮説に対する検定のp値です.有意水準0.05だといくつかの変数がオーバーしますが,0.1以内には収まっていることと,一番関連付けたい$${omr\_nc}$$のp値が非常に小さいことから,入力データは問題無いと判断しています.

3.2 結果
12週前までの過去の時系列データを探索範囲とすることと,主要な因果関係だけを残す枝刈りオプションをオンにして,新型コロナワクチン接種者数の年齢を,全年齢と65歳以上それぞれのデータセットを入力し,VARLiNGAMで因果探索を行いました.結果のパス図をそれぞれ図10,11に示します.パス図の読み方は私の過去のノートをご覧ください.
図10のコロナワクチン接種者数が全年齢の場合,新型コロナ死亡者を除く超過死亡率を示す$${omr\_nc(t)}$$に接続しているのは,$${omr\_nc(t-1)}$$と$${emg(t-2)}$$です.すなわち1週前の自己の超過死亡率と,2週前の救急搬送困難事例数が,超過死亡率に対してGranger因果を有していると解釈されます.平たく言えば,自己の過去の情報を除けば,2週前の救急搬送が超過死亡率を押し上げるという意味になります.また,その因果係数はそれぞれ,0.30,0.18となり,自己の過去の影響が相対的に大きいといえます.

同様に,図11の高齢者のワクチン接種者数に限定した場合,今度はパス図がやや複雑になります.$${omr\_nc(t)}$$に接続しているのは,$${omr\_nc(t-1)}$$,$${case(t-2)}$$,$${emg(t-2)}$$,$${vax34\_65(t-1)}$$であり,因果係数はそれぞれ,0.34,0.09,0.01,0.20となります.過去の超過死亡率を除けば,Granger因果を構成する最も大きな要因は,65歳以上の新型コロナワクチンのブースター接種であることがわかります.

先のパス図の因果係数から,超過死亡率を推計するモデルをそれぞれ以下のように書けます.
$$
Model 1:
omr\_nc(t)=0.3omr\_nc(t-1)+0.18emg(t-2) (4)
$$
$$
Model 2:
omr\_nc(t)=0.34omr\_nc(t-1)+0.09case(t-2)+0.01emg(t-2)+0.2vax34\_65(t-1) (5)
$$
ただしこれらは標準化後の推定式なので,標準化に使った各データのパラメータ(平均値,標準偏差)を用いて,標準化前の超過死亡率を逆残で推定しました(図12).2022年のほうが2021年よりも追随性が良いように見えます.

さらに,得られた$${超過死亡率(t)}$$から,式(1)によって$${実測死者数(t)}$$を推計しました(図13).

これらの推定精度を決定係数で評価した結果を表3に示します.いずれも,Model 2,すなわち,新型コロナワクチン接種者数を65歳以上に限定したモデルのほうが説明力が上がっています.

最後に,精度が高かったModel2を用いて,モデルの構成要素である,2週前の新型コロナ陽性者数($${case(t-2)}$$),2週前の救急搬送困難事例数($${emg(t-2)}$$),1週前の65歳以上の新型コロナワクチンのブースター接種者数($${vax34\_65(t-1)}$$)由来の死亡者と,当該週の新型コロナ死亡者数($${death_covid(t)}$$)を積み上げると図14のようになります.(モデルの変数に入っていない,1・2回目のワクチン接種由来の死者数は考慮されていないことに注意してください.)

この死亡者数を,新型コロナワクチンの3回目接種が開始される前後で集計したのが表4です.2022年8月28日まで,65歳以上のブースターワクチン接種による死者はおよそ8600名と推計されました.この数はかなり多いと思われるかもしれませんが,社会全体で新型コロナワクチン接種の負の面が報道され始めたのは最近であり共有されていないこと,データ1週分のタイムラグが最大2週間あること,2回目までの接種で無事であれば,新型コロナワクチンは安全と認識されやすい可能性があることなどから,医者や接種者自体がワクチンと死亡を関連付けにくい状況があって,報告されない潜在的な数としては,これぐらいあるのではないかと個人的には思っています.
今回はモデルを単純にするため,枝刈りを行って推定を行い主要な因果関係をのみを残したため,1・2回目の新型コロナワクチンの接種回数は変数として残りませんでした.そのため,表の?の部分が不明となっています.因果関係はともかく,公式発表では2021年12月3日までに1368人が新型コロナワクチン接種後に亡くなっています(リンク).かなりざっくりとした試算になりますが,以下のような2期の内訳の幾何平均を使うと,?の数は今回は2144人と推計されました.主観的な評価になりますが,桁感としてはありあえる数値だと思います.
$$
\sqrt[3]{\frac{8959}{20641}\frac{295}{3491}\frac{295}{947}}\times8614\simeq2144 (5)
$$

4. おわりに
本稿では,2021年1月3日から2022年8月28日までの,日本国内の新型コロナの流行,ワクチン接種,超過死亡率の間にある因果関係を,時系列データの因果探索手法であるVARLiNGAMを用いて推計しました.その結果,特に65歳以上の新型コロナワクチンのブースター接種者数が,2022年の超過死亡者数に対してGranger因果を有する可能性が高いことを示しました.さらに,最初のワクチン接種から2022年8月28日までに,1万人以上の国民がワクチン接種由来で死亡している可能性があることを示しました.
2022年8月末では流行が収束していないので,今後のデータの追加で結果が変わる可能性がありますが,現状としてわかったことを報告させていただきました.長文をお読みいただき感謝いたします.
