アインシュタインタイル「HAT」と「TURTLE」のあいだのタイルを愛でる。とにかく愛でてみる。

前回の記事はこちら。

ここ３回はアインシュタインタイル絡みで記事を書いておりますが、今回も書きます。

そういえば角度を見ていなかった

今回は、論文「An aperiodic monotile」から、１１ページにある、以下の図を話題にします。

引用：An aperiodic monotile p.11
Figure 2.3
https://doi.org/10.48550/arXiv.2303.10798

（Tile(x,x)と名付けている）単一のタイルを平面に敷き詰めた図です。
正三角形４個を組み合わせたTile(0,1)から、徐々に変形させて正三角形８個を組み合わせたTile(1,0)となります。
この中間の図形を作り出せるアプリが、前々回の記事で紹介した「Aperodic Tile Maker」になります。

ちなみに、Tile(1,$${\sqrt{3}}$$)は「HAT」、Tile($${\sqrt{3}}$$,1)は「TURTLE」です。

取り上げたいタイルは、この２つのタイルの中間にあたるTile(1,1)です。

余談：
Tile(1,1)は、「HAT」や「TURTLE」と異なり、Tile(0,1)やTile(1,0)と同じく周期的に平面敷き詰めができるタイルです。

で、このタイルってどんな形なのか、トレースしてみました。

これがTile(1,1)です。
少なくともわかっているのは、１辺をのぞいてすべて同じ長さ（残りの１辺は２倍の長さ）であることです。
角度ですが、Figure2.3をよくよく見ると特徴的でして、「HAT」と「TURTLE」もならべてみると、このようになっております。

左：「HAT」　中：Tile(1,1)　右：「TURTLE」

赤い丸は９０°、黄色い丸は１２０°です。
黄色い丸が２つあると２４０°、赤い丸が３つあると２７０°になります。
辺の長さだけを変化させているので、角度は変化していません。

「HAT」「TURTLE」と同様に、（辺の長さが同じなのでちょっと混乱しますが）、辺を適当な本数で区切り２つに分けて平行移動させると、２つの図形ができます。

こいつも「ヘリコプター」だった

さて、そもそもこの一連のアインシュタインタイルの記事を書いているのは、「HAT」が２つの点対称の図形に分割できることに気づいたことです。

そうなると、Tile(1,1)も同じではないか、と思うわけです。

なっておりました。

しかも、「HAT」「TURTLE」と異なり、回転主翼（黄色）は点対称どころか線対称です（それゆえ、周期的敷き詰めになってしまうわけです）。
さて、ここで気になるのは、２つの図形の大きさです。
注目したいのは、それぞれの図形に引いた赤線の長さです。

似ているようで似ていないプロペラ

前の章の２つの図形を引いた赤線で切り取ると、それぞれ五角形の図形――回転主翼および回転尾翼のプロペラ――が取り出せます。
それぞれの特徴も取り出して、補助線をさらに引くと下のようになります。

左：回転尾翼のプロペラ
右：回転主翼のプロペラ

赤い丸は９０°で、黄色い丸は１２０°。
しかも、印をつけた角度を挟んでいる辺は同じ長さなので、二等辺三角形になっています。

左（回転尾翼のプロペラ）の五角形の一番上の頂点の角度は１２０°なので、赤い二等辺三角形の一番上の頂点は、（120-45-45=）３０°です。
右（回転主翼のプロペラ）の五角形の一番上の頂点の角度は９０°なので、赤い二等辺三角形の一番上の頂点は、（90-30-30=）３０°です。

つまり、２つの図形の赤い二等辺三角形は相似でして、比率は、

回転尾翼のプロペラ：回転主翼のプロペラ＝$${\sqrt{2}}$$：$${\sqrt{3}}$$

です。

……なのですが、回転主翼を五角形で切り出してしまうと、

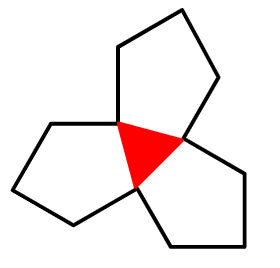
正三角形の部分が余ってしまいます。
なので、下の左図のように、正三角形三等分の図形を付け足して、プロペラを六角形にします。

付け足した部分の青の辺２本分の長さですが、３０°−６０°−９０°の直角三角形の関係より、赤の辺の$${\frac{2}{\sqrt{3}}}$$倍になります。

結局、それぞれの図形を二等分、もしくは三等分したプロペラにあたる図形の接合している辺の比率は、

回転尾翼：回転主翼＝$${\sqrt{2}}$$：1

となります。
意外とスッキリしました（とはいえ、$${\sqrt{2}}$$が残ってしまうのは、$${\sqrt3}}$$とあわせて無理数が２種類あり、おそらく扱いが面倒なんですよね）。

締め

ということで、今回は（特になにか適当な名称がつけられていない）Tile(1,1)を愛でてみました。

ここまでくると、残っているTile(1,4)とTile(4,1)も愛でないといけないかも、と思ってしまいます。
ちなみに、Tile(1,4)とTile(4,1)のどちらも「非周期性モノタイル」になるとのことです。

次回どうしましょうかね。

では。