媒介変数表示された関数の第二次導関数の分からなかったところ

　こんにちは。

　新年あけまして、おめでとうございます。
　今年もよろしくお願いいたします。

　新年一発目の記事は、ゴリゴリの数学記事になります（笑）
　最近数学検定1級の勉強をしているので、このような記事が多くなっちゃいますね。

１　躓いた問題

　私が躓いたのは、以下の問題です。
　これは、数学検定１級準拠テキスト微分積分　中村力著　の問題です。

問題

　(1)は、高校の基礎レベルの問題で、これは解けました。
　$${\frac{dy}{dx}=\frac{t^{t-1}(\log{t}+1)}{2}}$$
　で、$${t=e}$$における$${\frac{dy}{dx}}$$の値は、$${e^{e-1}}$$です。

　問題は(2)です。
　私の誤っていた考え方を紹介します。

・　私の誤った考え方

私の誤った考え方

　このような考え方をしていました。
　でもよく見ると、もし$${dt^2}$$同士で約分できたとしても、残るのは$${\frac{d^2y}{d^2x}}$$だから、$${\frac{d^2y}{dx^2}}$$と等しくないですね。
　よって、この考え方は誤りです。

２　第二次導関数の正しい認識

　躓いたときは、基礎に戻りましょう。

　第二次導関数とは、導関数において、$${x}$$の微小な変化に対する$${\frac{dy}{dx}}$$の変化の割合です。
　式でかけば、こうなります。
　$${\frac{d^2y}{dx^2}=\frac{d}{dx}(\frac{dy}{dx})}$$

　右辺の式は、$${\frac{dy}{dx}}$$を$${x}$$で微分すればよいことを言っています。ただ、今回は媒介変数表示されているため、工夫が必要です。

・　媒介変数表示された関数の第二次導関数の求め方

　今回、（第一次）導関数$${\frac{dy}{dx}}$$は、媒介変数$${t}$$で書かれています。
　これを$${x}$$で微分したものが第二次導関数$${\frac{d^2y}{dx^2}}$$です。$${t}$$で書かれた式は$${t}$$で微分するのが、一番簡単ですよね？

　なので、次のような式に変形します。

式変形

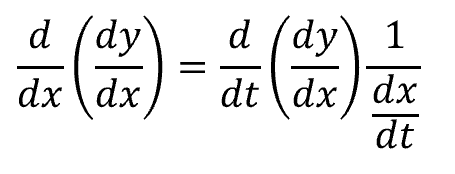
　このようにすれば、$${\frac{dy}{dx}}$$を$${t}$$で微分できます。右辺の$${\frac{1}{\frac{dx}{dt}}}$$は、「＝」にするための帳尻合わせです。

　この式を使って、躓いた問題をもう一度解いてみます。

３　躓いた問題をもう一度解く

　上で示した式変形を用いて、もう一度第二次導関数を求めます。

第二次導関数を求める過程

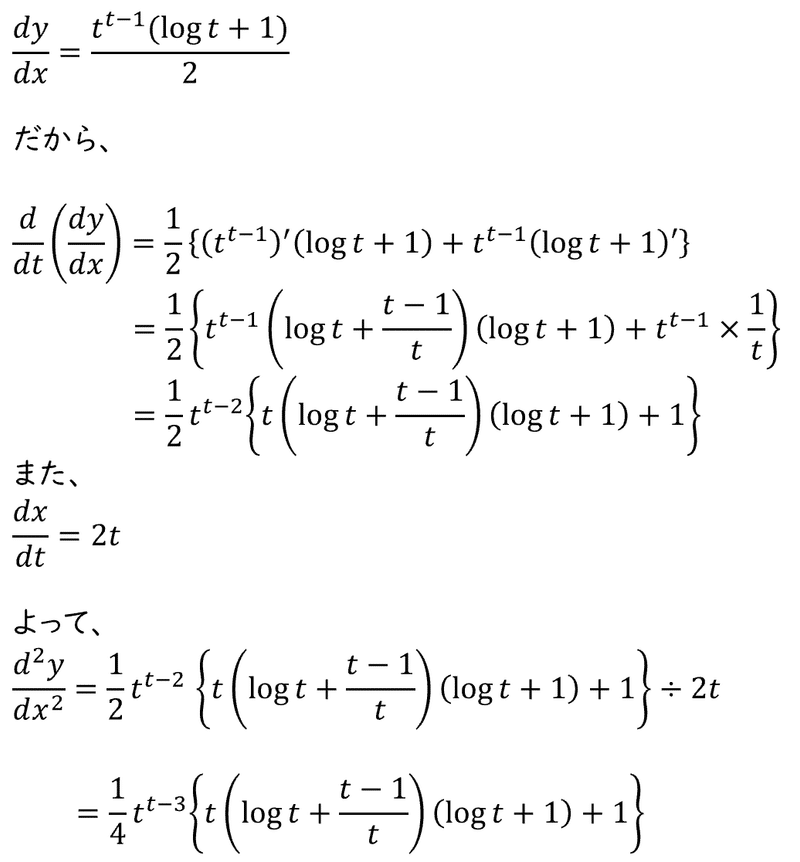
　問題は$${t=e}$$における$${\frac{d^2y}{dx^2}}$$の値なので、

t=eにおける第二次導関数の値

４　おわりに

　今回の問題から、分からないときは一度基礎に戻って定義を見直すことの大切さを教えてくれました。

　理解したと思っていても、少し複雑になると分からなくなることはありますね。でも、それを解決できた時は、以前より理解を深められます。

　最後まで読んでいただき、ありがとうございます。