#2 【非日常の数学】 なぜ怪人は単独で活動するのか?
ヒーローものの映画や番組を観てみると、毎度新しい怪人が街で暴れ、ヒーローと戦い、最後はヒーローにやられるという展開がおなじみです。でも、もし怪人どうしが協力すれば、やられずに済むかもしれません。少なくとも1人の時よりは街を破壊することはできるはずです。では、なぜ怪人は協力し合わずに単独行動をするのでしょうか?この疑問に答えるべく、怪人の行動をモデル化してみました。
※ いわゆるギャグ的な内容ですので、ゆる〜くお楽しみください。
※ 本内容をPDFでキレイにまとめたものを本文の最後にリンク掲載していますので、そちらもぜひ御覧ください。
※ 本文は全て読めますが、「投銭」として最後に購入ボタンを設定していますので、気に入っていただけましたら応援宜しくお願いします。
はじめに
誰しもが一度は憧れるであろうヒーロー。その一方で、ヒーローをヒーローたらしめているのは、敵となる怪人の存在だ。毎度毎度新たな怪人が現れて、街を破壊し、時にはヒーローをピンチに貶める。しかし、どんな怪人であれ、最後はヒーローにやられ、塵と消えていく…。
そんな怪人たちを見て、きっと誰しもが、一度は「なぜこの怪人たちは単独で活動するのだろうか?協力すれば良いのに」と疑問に思ったことだろう。そこで本著では、そうした疑問を解決するために、いくつかの仮定の下、なぜ怪人どうしが協力しないのかを示す。
怪人の目的は?
そもそも、怪人の目的は何だろうか?少なくとも、ヒーローと戦うことではないだろう。では、なぜヒーローは怪人と戦うのか?それは、ヒーローは街の平和を守る存在であり、怪人たちが街で破壊活動をしているのを止めるためである。すなわち、怪人がやりたいこととは《街を破壊すること》であることが分かる。
きっと、怪人は自らの手で街を破壊することで快感を得ることができるのであろう。そこで、すべての怪人が《利己的な存在》として、以下の目的をもって行動すると仮定しよう。
怪人の目的: 自らが破壊する街の面積を最大化したい
怪人は《利己的な存在》なので、他の怪人がどれだけ街を破壊したかには興味はなく、あくまでも自分自身の破壊でのみ快感が得られるとする。
怪人の行動のモデル化
それでは、怪人の行動をモデル化し、本当は協力した方が得なのかどうかを考えていくことにしよう。これを判断するには、怪人が1人の時に自分が街を破壊できる面積の期待値と、もう1人に協力を仰いで2人になった時の、自分が街を破壊できる面積の期待値を比較すれば良い。
簡単のため、もう1人の怪人は自分と同じ強さであるとし、怪人が単位時間あたりに破壊できる街の面積を v(t) として話を進める。また、(どんな怪人も最終的にはヒーローに倒される運命だとして)怪人がヒーローに倒されるまでの時間を T とする。
さて、まずはシンプルに v(t) が常に一定値 V、すなわち怪人は常に同じ面積を単位時間あたりに破壊し続けるとして考えてみよう。この時、怪人が自分だけの時の破壊量の期待値 E は次のように表すことができる。
![]()
一方、怪人がもう1人いたとするとどうなるだろうか。ヒーローは 50% の確率でそちらの方を先に倒しに行き、この場合は自分が倒されるまでの時間は 2T となるから、自身の破壊量の期待値は次のようになる。
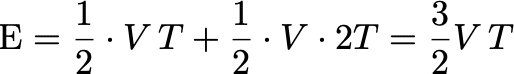
よって、単位時間あたりの破壊量が常に一定値 V であるならば、怪人どうし協力した方が、より自身の欲求を満たすことができる可能性が高い。
しかし、話はそう単純ではない。実際には単位時間あたりの破壊量 v(t) を常に一定値で保つというのは難しいからだ。街を破壊していけばいくほど、新たに破壊できる場所は減っていくため、どうしても単位時間あたり破壊量は減っていってしまう。すなわち、単位時間あたりの破壊量は、街の残り面積と比例関係にあると言える。
よって、街の残り面積を s(t) とすると、怪人が1人の時は次の式が成り立つ。ただし、式中の γ は比例定数 (< 1) である。
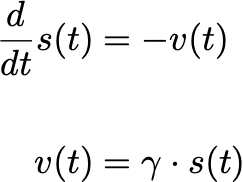
これはつまり、先ほどは破壊量を《一定値》で考えたが、今回は《一定割合》と仮定して考えていることになる。これら2式より、s(t) に関する次の微分方程式が得られる。
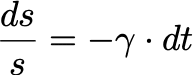
よって、s(0) = S (= 街全体の面積)とおくと、s(t) と v(t) に関する次式が得られる。
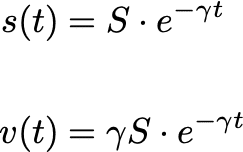
これにより、怪人1人のときの破壊量の期待値 E は次のようになる。
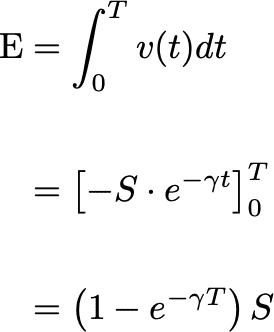
一方、2人の場合はどうなるかと言うと、怪人の強さは同じだと仮定しているので、s(t), v(t) はそれぞれ次式を満たす。
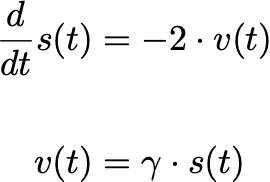
ここから、先ほどと同様に微分方程式を解くと、下式が得られる。
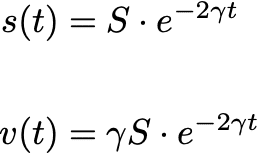
ただし、もう1人の怪人が時刻 T で倒されてしまった後は自分1人になるため、
![]()
であることを踏まえると、それ以降(t > T)では下式となる。
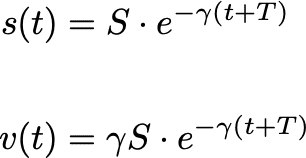
よって、怪人が2人のときの破壊量の期待値 E は次のようになる。

これで、1人の時と2人の時の期待値がそれぞれ最終的に下式のように求まったので、これら2つの大小を比較すれば良い。
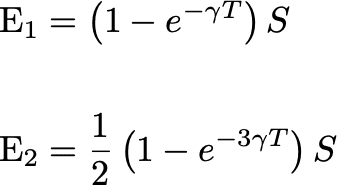
なぜ怪人は単独で活動するのか?
さて、先ほど求めた期待値を用いて、怪人が1人のときの方が得られる期待値が大きいと仮定して計算みよう。
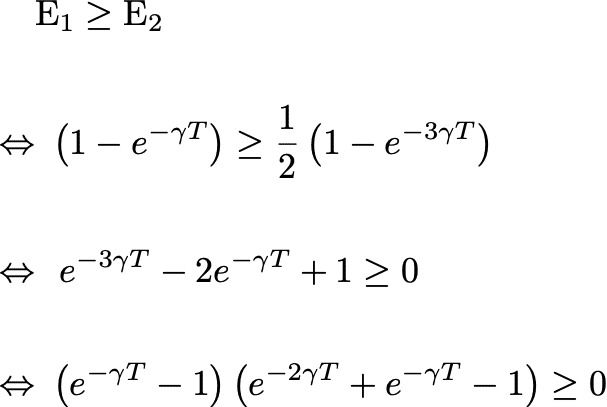
ここで、
![]()
であることに注意すると、
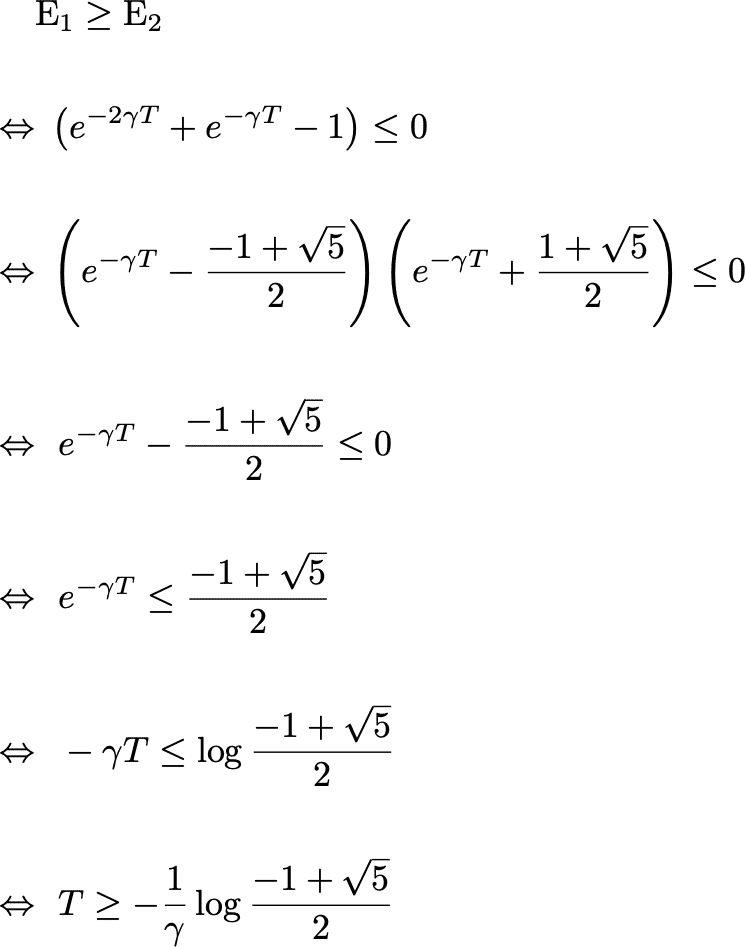
という不等式が得られる。更に、
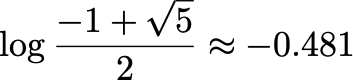
として計算すると、
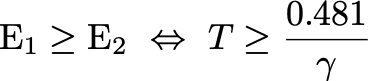
が最終的に得られる。
これはすなわち、自分が破壊活動する時間が長いほど、1人で活動する方がより満足できるということを表しており、確かに怪人自身は(ヒーローに倒されることなど夢にも思わず)ずっと破壊活動を続けられると信じているだろうから、怪人が単独で活動するのはとても合理的な選択だと言えることが分かった。
おわりに
本著では、なぜ「怪人は単独で活動するのだろうか?」という疑問を解決するために、怪人の行動をモデル化・そこから得られる期待値を計算し、確かに単独で活動する方が得られる満足度は高くなる可能性が高いことを示した。
いつもヒーローに倒されてしまう怪人たちであるが、その裏には合理的な行動の選択があるということを意識することで、よりヒーローと怪人の戦いに関心が持てるようになるであろう。
リンク
※ PDFのリンクはこちらです。(A5 / 12ページ)
※ 内容は以上が全てです。これ以降文章はありませんが、「投銭」として最後に購入ボタンを設定しています。気に入っていただけましたら応援宜しくお願いします。
ここから先は
¥ 110
この記事が気に入ったらサポートをしてみませんか?
