『凝縮系物理学』§3:金属における磁気秩序
§3.1 磁性を示すのはなぜか?
磁性を示すのは、原子の磁気モーメント同士の間にそろえようとする相互作用があるからである。この「そろえようとする相互作用」を交換相互作用と呼ぶ。
基礎となる電子のハミルトニアンは、運動エネルギー(電子の運動)+ポテンシャルエネルギー(クーロン相互作用)である。クーロン相互作用は電子と電子が反発しあう力で、電気の話であり、直接は磁気モーメントと関係なさそうに見える。これらの項が磁気モーメントとどう関係するかをまず理解する必要がある。
一番簡単な例は、水素分子である。1つの電子をもつ水素原子が2つくっついたときに、エネルギー準位は一重項と三重項に分かれる。このとき、一重項はS=0であり、三重項はS=1である。スピンがない一重項状態の方が(波動関数の重なり積分が大きくなるため)エネルギーが低くなり、2つの電子は一重項状態をとる。このようにクーロン相互作用(とパウリの排他律)の結果、スピンの状態が選択される。
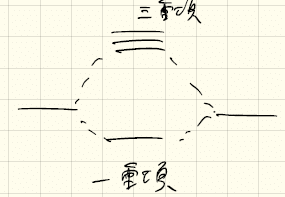
一般に、運動エネルギーとポテンシャルエネルギーの間には、以下のようなトレードオフの関係にある。
運動エネルギーは、完全に電子が局在するよりも隣に飛び移ったほうが得である。飛び移りにはパウリの排他律より反平行スピン状態が好まれる。(先ほどの水素分子の例)
↕
一方、波動関数が重なると、反平行スピンならパウリの排他律には反しないが、クーロン相互作用は損をする。この意味では平行スピン状態の方が好まれる。(実際に原子内ではスピンは平行にそろうのだった)
上記のトレードオフがどちらのスピン配置が安定であるかを考えるときの基本となるが、実際には物質によって磁性の機構は異なり複雑である。(例えば、Fe金属では電子が動くことが強磁性発現に重要である一方で、Fe酸化物は絶縁体で電子は動かない。酸化物の場合は、酸素イオンを媒介としたモデルで磁性が説明される。)電子の飛び移りにはスピンの反平行が有利、と述べたが、実は、電子がバンドを組んでいる場合には、(となりの原子の波動関数と直交しないため)必ずしもそうではない。強磁性的に電子が飛び移る場合もあり得る。強磁性と反強磁性のどちらが安定かは、d軌道の空席がどういう状況なのかにも依存する。このような細かいところは本授業の対象外なので以下では省く。
§3.2 Feはなぜ強磁性をもつのか?
Fe(1s)2(2s)2(2p)6(3s)2(3p)6(3d)6(4s)2を例にとると、(3d)6が磁性に関わり、(4s)2が結晶中を伝搬する。イメージを描くと以下のようになる。
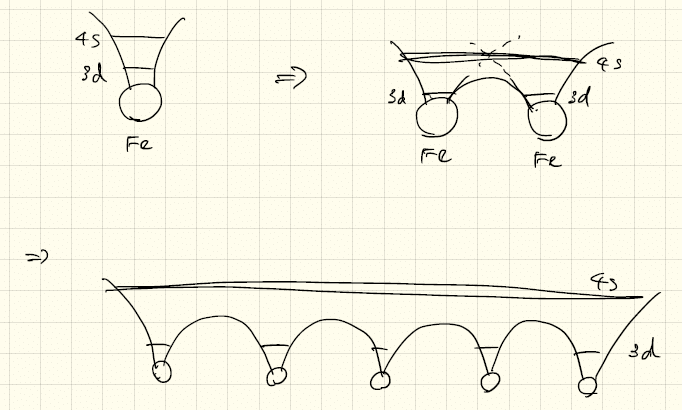
4s電子は原子核の束縛を離れ、周期ポテンシャルを感じながら自由に運動する。一方、3d電子は1つの原子の3d軌道上に十分長く滞在してから隣の原子にトンネル効果で移る。運動エネルギーの小さい3d電子の方が相対的にクーロン反発エネルギーが大きく、磁性の発現に重要となる。
金属においては、絶縁体の磁性とは異なり、隣り合う原子間を電子が飛び移る描像は現象論的な取扱いに過ぎない(3d電子もエネルギーバンドを作っている)。それでもある程度の時間は原子に滞在しているから、磁性の記述によい近似となる場合もある。よく言われる「3d電子はある程度局在している」ということである。
Feの強磁性はストーナー理論で説明される。ここでは直感的な説明を与える。5つあるd軌道は一種類のみと仮定してモデル化する。つまり、一つのサイトには電子は2つまで入り、例えばMn(3d^5)の場合は、一つの電子が入っていることになる(n=1)。
下図のようにバンドを考え、電子を下からつめたとする。そのとき上向きスピンだけでつめた場合よりも、上下スピン電子をセットにして詰めた方がフェルミエネルギーが低くなる。つまり、上下スピン電子をセットにして詰めた方が、運動エネルギーは低くなる。よって、電子スピンがそろうと(強磁性になると)、運動エネルギーは損をすることになる。一方で、クーロン反発のエネルギーは強磁性の方が得をする。(これは先ほどのトレードオフの話を言い換えただけである。)

以上の考えを簡単なモデルを使って計算する。

全原子数をNとし(全サイト数2N)、全電子数をnとする(上/下向きスピン電子n/2個ずつ)。1つのサイトに電子が2つ存在するときのクーロンエネルギーの損失は、(全原子数)×(1つの原子に2つの電子がある確率)×Uなので
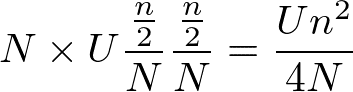
である。(1つの原子に1つの電子がある確率は1/Nであり、上/下向きスピン電子はn/2個ある)。もし強磁性になっていて、上・下向きスピン電子数をn_↑、n_↓(n_↑>n_↓)とすると、エネルギー損失は
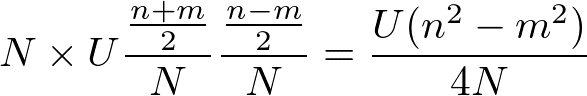
となる。ここで
![]()
とおいた。以上より、強磁性になったときのクーロンエネルギーの利得は
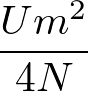
である。一方、運動エネルギーの損は、強磁性になったときに
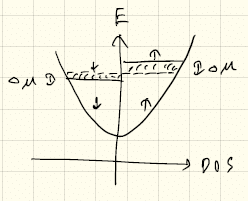
減ったスピンの電子数=増えた上向きの電子数=D(E_F)Δμ がエネルギー上昇Δμしたとして、
![]()
また
![]()
なので、
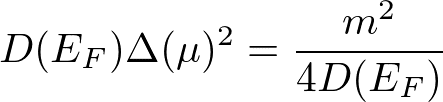
1原子当たりだと
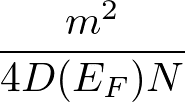
である。
以上より、強磁性が出るためには、クーロンエネルギーの得が運動エネルギーの損以上であることが必要なため、
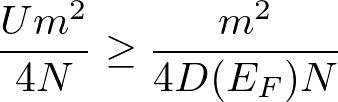
整理すると、
![]()
となる。これがストーナー条件である。強磁性が安定になるには、クーロン反発エネルギーが大きいほどよく、フェルミ面での状態密度が大きいほどよいことになる。
§3.3 反強磁性金属
反強磁性も状況によっては同じモデルで説明可能である。クーロン相互作用が運動エネルギーよりも非常に大きく(U/t>>1)、また電子数=原子数 (n=N)の場合を考える。このとき、全原子に一つずつ電子が入っていることになる。この場合は、以下の理由で、スピンが上向きと下向きで交互に並ぶ反強磁性が安定になる。
反強磁性配列だとパウリの排他律は反さないので、電子は飛び移り可能である。しかし、クーロンエネルギー>>運動エネルギーなので、運動エネルギーの得が少なく絶縁体になりそうだが、量子力学的には以下の電子遷移(一度となりの原子に電子が移って戻ってくる過程)が可能である。

この過程は、運動エネルギー(tとおく)を摂動として加えた状況であり、

と評価できる。ここで、|0>はクーロン相互作用Uに対する基底状態(各サイトに1つずつ電子がある状態①)で、E_0はその固有値である。|n>は、上図の②に相当し、電子が2つあるサイトが存在する状態である。エネルギーE_nはE_0=0として、E_n=Uと評価できる。上式の摂動計算は、①→②→③の過程を表している。
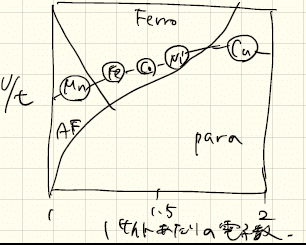
このようにU>>tではあるが、電子が隣に飛び移ることによるエネルギーの利得があり、これが反強磁性発現の1つの起源となり得る。実際に、金属Mnでは反強磁性が生じることが知られている。以下の図が3d金属のおおざっぱな相図である。1サイト当たりの電子数が1に近くてU/tが大きいMnだと反強磁性、n>1のFe,Co,Niで強磁性(状態密度の特異性も必要だが)、n=2で3d軌道は全部詰まって常磁性(Cu)になる。ここで、5つある3d軌道は一種類のみと仮定していることに注意せよ。
§3.4 金属における常磁性と反磁性
磁性の観点から金属を分類すると以下のようになる。
[A]ふつうの金属:強磁性や反強磁性にならないもの。磁化は温度によって余り変化しない。例として、アルカリ金属K, Naや貴金属Cu, Ag, Au、その他Al, Tl, Zn, Cd, Hg, Mg, ...など多くある。アルカリ金属K, Naや貴金属Cu, Ag, Auにおいては、内殻の電子が閉殻になっており(→反磁性)、外殻のs電子が1つある(→常磁性)。常磁性と反磁性が足し合わせになっており、通常は反磁性が強いことが多い。
[B]磁気的に興味ある金属:不完全電子殻をもつ原子からなるもの。3d(Sc~Ni)、4d(Y~Pd)、5d(La~Pt)は、s電子が伝導電子でd電子がある程度局在している。特に、3d金属が磁性を示す。また、PdやPtは磁化が大きめで温度変化も大きい。強磁性に近い金属と呼ばれており、実際に少量のFe,Coドーピングにより強磁性が発現する。もう一つの例は、4f殻をもつ金属で、希土類金属と呼ばれる。s電子が伝導電子であり、f電子は局在している。
この節では、常磁性と反磁性の起源を説明する。
常磁性には、(1)スピン常磁性(パウリ常磁性)と(2)軌道常磁性(ヴァンブレック常磁性)の2つがある。
(1)スピン常磁性(パウリ常磁性):磁場をかけると、ゼーマン効果により上/下向きスピン電子数に差が生じる。ゼーマン効果により、上向きスピン電子バンド +μ_B H、下向きスピン電子バンド -μ_B Hだけエネルギーが変化するので、エネルギー差は 2μ_B Hである。また、誘起される磁化は、上/下向きスピンの電子数差ΔN×μ_B で与えられる。
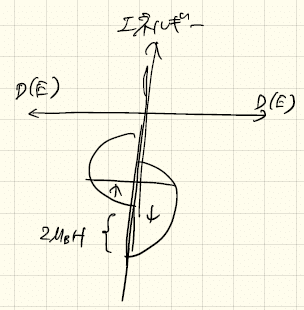
ゾンマーフェルト展開を使って計算すると、帯磁率χ_pは

となる。第一項は、フェルミエネルギーの状態密度に比例した常磁性磁化であり、磁化は磁場に比例して増大する。温度の項は含まれず、温度変化しないことがわかる。第二項はsバンドだと小さいが、dバンドだとdバンドの幅が狭いため状態密度が大きく、その二階微分も大きい場合がある。PtやPdがその例であり、帯磁率の温度変化が大きい。
(2)軌道常磁性(ヴァンブレック常磁性):軌道角運動量は通常消失しているが、少し複雑な機構で常磁性が出る場合がある。軌道常磁性を簡単に説明すると以下のようになる。
磁場をかけると、ゼーマン効果の摂動によって、上の励起状態が基底状態に混ざることで、基底状態に少し軌道角運動量が現れる。スピン-軌道結合により、磁気モーメントは少し大きくなる。(ゼーマン効果とスピン-軌道相互作用を摂動にとる。)
電子が詰まっていない準位数N_u、電子が詰まっている準位数N_0とおき、詰まっている/いない準位間のエネルギー差をΔEとおく。ΔEは熱励起できないくらい大きい。

このとき、ヴァンブレック常磁性の帯磁率χ_vvは
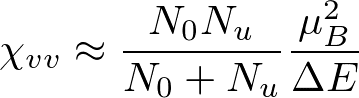
と書ける。この式をみると、温度変化は一定である。d軌道が半分空いている場合(d電子が5個の場合)がχ_vvが最も大きい。例えば、3d金属だとV、Cr、β-Mn、4d金属だとNb、Mo、5d金属だとTa、Wが、χ_vvが大きい。(全部がd5の状況ではない。)
次に、反磁性の起源を説明する。反磁性は、(1)閉殻電子に由来する起源と(2)伝導電子に由来する起源がある。
(1)閉殻電子の反磁性:閉殻電子は反磁性を示す。磁場をかけたことにより電子はサイクロトロン運動するが、環電流による磁気モーメントが磁場とは反対向きであるため、反磁性を示す。
以上を定式化する。磁場をz向きにかけるとする。ファラデーの法則
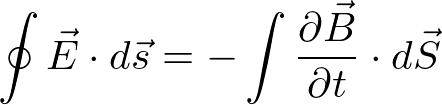
より、電子のサイクロトロン運動の半径をRとして
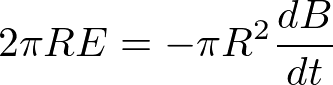
と書ける。よって電子にかかる電場は
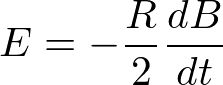
である。この電場によって生じる速度の時間変化は
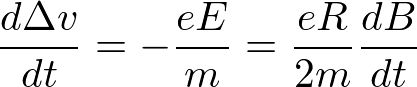
よって
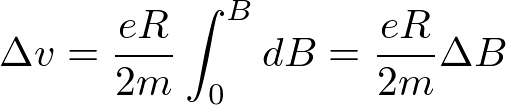
となる。環電流は
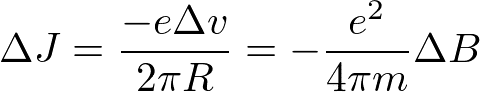
と書けるので、磁気モーメントとして
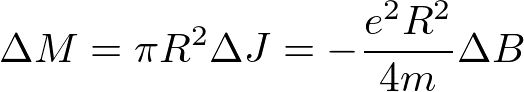
を得る。閉殻の電子の場合、Rは大体、原子核まわりの電子の波動関数の広がりの程度と見積もられる。
(2)伝導電子の反磁性(ランダウ反磁性):伝導電子は常磁性に寄与するが、反磁性も出す。伝導電子の磁場中のサイクロトロン運動を量子力学的に取り扱うと、磁場に直交した2次元面でのエネルギー固有値は量子化される(ランダウ準位)。このとき、温度のエネルギースケール>>磁場のエネルギースケールの仮定のもとでの計算によると反磁性の帯磁率χ_dは
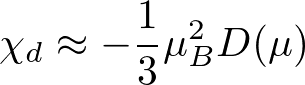
である。パウリ常磁性の1/3で符合が反対である。
以上をまとめると、ふつうの金属の帯磁率は、
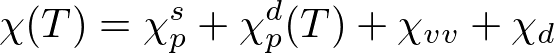
と書ける。順に、s電子によるスピン常磁性、d電子によるスピン常磁性、d電子による軌道常磁性、伝導電子および内殻電子による反磁性である。第二項がもっとも温度変化が大きいと考えられるので、(T)とつけた。
この記事が気に入ったらサポートをしてみませんか?
