力学§４：運動の解析

実際に質点の運動を解析する。運動が運動方程式で規定される以上、方針としては、微分方程式である運動方程式をどうやって解くか、が基本になる。保存則が使える場合には、有効に使うことで解析が簡単になることがある。

§４．０　微分方程式の解き方

我々の扱う微分方程式は、

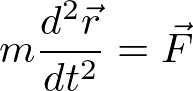
である。二階微分が含まれているので、二階の微分方程式と呼ばれる。右辺の力Fは、どのような力を考えるかで状況がわかれる。これから考える状況を整理すると、①定数項（重力など）、②位置ベクトルrに比例する項（ばねの弾性力など）、③速度ベクトルvに比例する項（粘性抵抗）が含まれる可能性がある。それぞれの状況によって、方程式の解き方が異なってくる。なお、Fが定数項を含まない場合、同次方程式と呼ばれる。

上記の方程式は、天下り的であるが、以下のように解くのが基本方針である。

（１）二階の微分方程式の解は、２個の独立な解を見つければよい。解は、２個の決定できないパラメータをもつ。

（２）非同次方程式（Fに定数項が含まれる場合）の解は、同次方程式の一般解に、非同次方程式の１つの特解を足せばよい。

（３）同次方程式

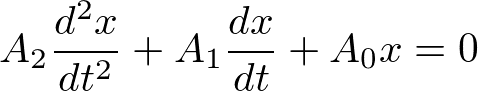
の解は、解の形を

と仮定して代入することで解ける（λの二次方程式が出てくるので、2個の独立なλが得られる）。つまり、解は

の形をしている。C_1とC_2は決定できないパラメータである（初期条件が与えられていたら決められる）。もし、λを決める式に重根があった場合は、

が解になる。

まとめると、同次方程式の解法（３）が基本的にまずやる作業で、それを利用して非同次の場合も解く。

§４．１　単振動

ばねの弾性力を受けて一次元運動する質点の運動方程式は

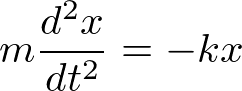
で与えられる。この方程式は、定数項を含まないため同次方程式である。§４．０の方針に従い、e^λtを代入すると、

となり、

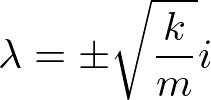
が得られる。解は

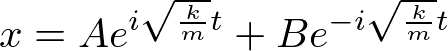
となり、解が実数となるようにAとBを取り直すと

という形に帰着される。適宜、未知パラメータを取り直しており、これらは運動の初期条件から決定される。

xの時間依存性は振動的であり、質点は振幅D_1で往復振動し、振動の周期は、

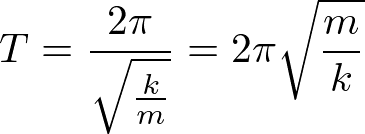
で与えられる。

問４．１　（１）上記のTの次元が「秒」になっていることを確認せよ。（２）この系の力学的エネルギーを求めて、保存することを確認せよ。

§４．２　減衰振動

単振動に粘性抵抗がはたらいて振動が止まる場合を考える。粘性抵抗は速度に比例するとして、

が運動方程式である。この式も同次方程式である。粘性抵抗の係数に2が入っているのは解を求めるにおいて楽になるように便宜上入れただけである。

解を求める方針に従い、e^λtを代入すると、

これはλに関する二次方程式であり、

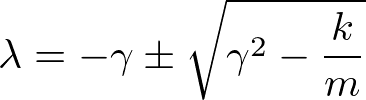
である。重根がない場合とある場合で、場合分けが必要である。

（１）粘性抵抗が大きいとき、つまり

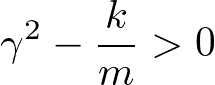
のとき、上記のλは２つの独立した実数解なので、一般解は

である。ともに指数の肩の（ ）内は正の実数であり、減衰する項である。

（２）粘性抵抗が十分小さいとき、つまり

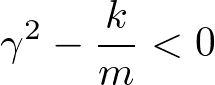
のとき、√の中が虚数になるので、

xは実数なので、AとBはxが実数になるものに限定される。

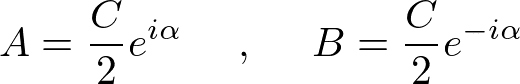
とおいて、

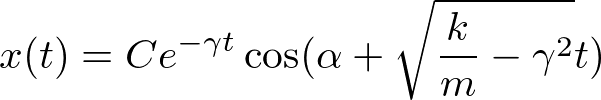
が得られる。振動の振幅がゆるやかに減衰しながら、振動する。これを減衰振動と呼ぶ。

（３）√の中がゼロになり、λが重根をもつとき、つまり

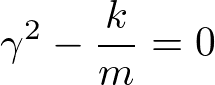
のときは、§４．０の微分方程式の解き方の方針に従うと、解は

で与えられる。これも減衰する解である。

問４．２　３つの場合における、それぞれの運動がどのような時間変化をするか図示せよ。特に、(1)の場合と(3)の場合は共に時間発展に対して減衰する解であるが、どちらが急激に減衰するか。（図は例えばここにある）

§４．３　粘性抵抗がある場合の落下運動

重力による落下運動において、抵抗がある場合を考える。運動方程式は

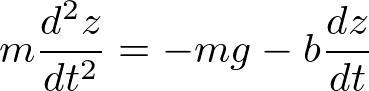
である。ここで、ｚ軸の正方向を鉛直上向きにとり、b>0である（落下の速度が下向き（負）なので、粘性抵抗は正符合（上向き）になる）。この方程式は、非同次方程式なので、§４．０の方針に従い、まずは定数項を無視した同次方程式の解を求める。

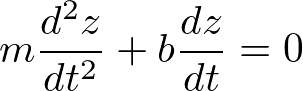
の一般解は、e^λtを代入して、

が得られるので、一般解は

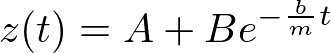
である。次に定数項を加えた非同次方程式の特殊解を考える。特殊解として、

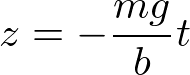
があるので、足すと、一般解

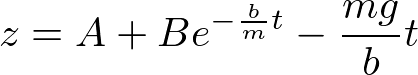
が得られる。

初期条件として、t=0でz=z_0、dz/dt=0とすると、AとBが以下のように定まる。

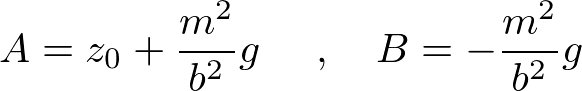
よって、

速度は、時間で微分して、

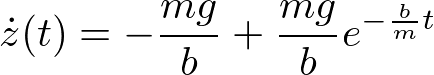
である。tが大きいとき、落下速度は、-mg/bに近づく（終速度）。

§４．４　振り子

鉛直方向を含む二次元面内で振り子運動する質点を考える。二次元極座標で考えた方が楽であり、この場合の運動方程式は、

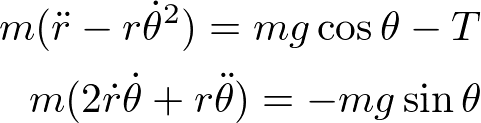
である。rが振り子の糸方向、θは振り子の回転角を表す。Tは張力である。振り子の糸は伸びないとすると、r=l（一定）で、

なので、運動方程式は

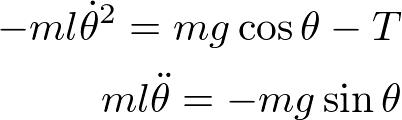
となる。二番目の式から振り子の回転角の時間依存性が求まる。回転角が小さいと仮定する（θ<<1）と、

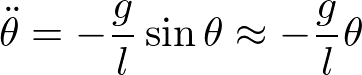
と単振動の式に帰着される。振り子の振動の周期は、単振動の場合と同様の求め方により、

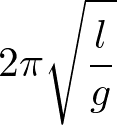
となる。糸の長さが長いほど、振り子の振動周期は長くなる（振動の振幅には関係しない）。また、解を運動方程式の第一式に代入すると、張力Tを求めることもできる。

§４．５　惑星の運動

地球が太陽の周りを公転するような場合を考える。この場合にはたらく力は万有引力である。

運動方程式を解く前に、惑星の運動に関して成立するケプラーの法則は以下の３つである。

（１）各惑星は、太陽を焦点とする楕円軌道上を運動する。

（２）静止した太陽と運動する惑星を結ぶ動径が単位時間に通過する面積は、惑星の軌道上の位置によらずに各惑星ごとに一定値である。（面積速度一定の法則）

（３）楕円軌道の長軸半径の３乗と周期の２乗の比は、全ての惑星で同じ値である。

さて、惑星の運動は回転運動であるので、公転軌道面（xy面）における２次元の極座標系で考えるのがよい。r方向の運動方程式は、

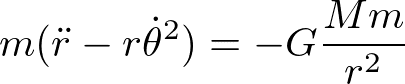
である。万有引力は中心力なので、角運動量は保存する。つまり、

が定数となる。

は面積速度一定の法則を表している。hを使ってr方向の運動方程式を書き換えると、

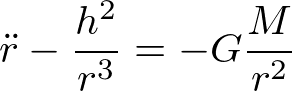
となる。求めたいのは、r=r(θ)である。

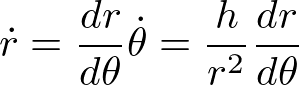
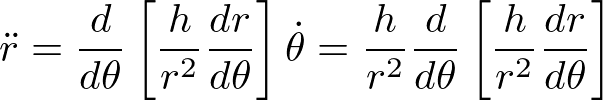
を用いると、

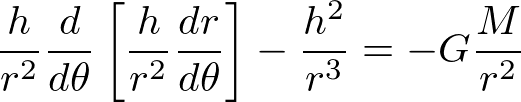
よって

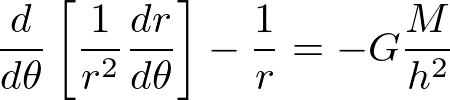
変数変換u=1/rを行うと、

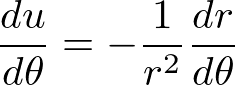
より、

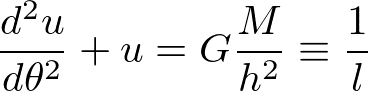
と変形できる。ここで、右辺は定数なので、それを1/lとおいた。

この微分方程式は非同次である。まず、右辺がゼロの同次方程式の一般解は、単振動と同じ形なので、

と求まる。非同次方程式の特解として、

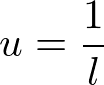
があるので、非同次方程式の一般解は、

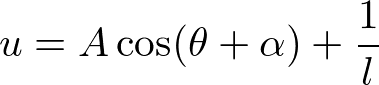
と求まる。未知パラメータAとαを

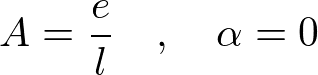
と（ある数eを使って）おくと、

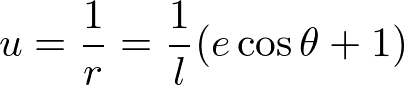
よって、

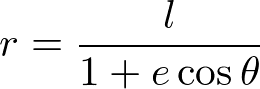
が得られる。eは離心率と呼ばれる。e=0のときに、rは定数であり、円運動を表す。0<e<1のときには楕円運動になる。また、e=1で放物線運動、e>1で双曲線運動となる。