『物性物理学１』§３：周期ポテンシャル中の「波」としての電子

（１）分子から固体へ

２原子分子（水素分子H2^+）を考える。つまり、以下の通り、１個の電子をAとBが共有している（共有結合）。

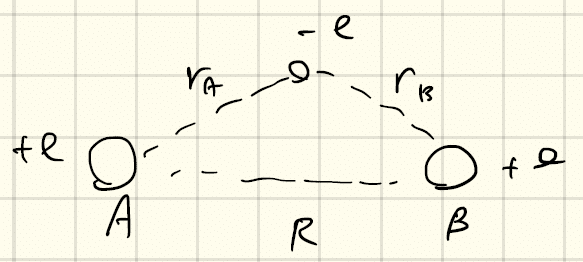
この系のハミルトニアンは、

である。Hψ=Eψの解（つまりエネルギー固有値）を求めたいが、厳密には解けない。

それぞれの１ｓ軌道の線形結合

を波動関数として仮定する。ここで、電子の電荷分布はAとBで対称なので、

よって

なので、取り得る波動関数は

の２つある。ここで、N_+とN_-は係数である。この波動関数を用いてエネルギー期待値を求める。

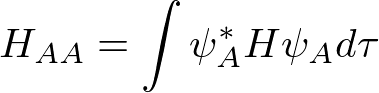
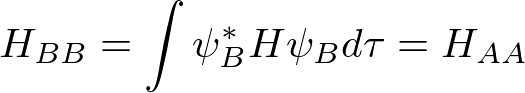
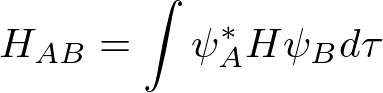
とおいて、

と書ける。（このような単純な系では）H_AAもH_ABも負なので、

となる。これは水素原子が２つ結合すると、結合性軌道と反結合性軌道に分かれることを意味している。図で描くと下のようになる。AとBの間に電子が多くいたほうが、原子核からの静電引力によるポテンシャルエネルギーが低くなる。

この例から学ぶべき教訓をまとめると、次の通りである。自由な原子は、離散的なエネルギー準位1s, 2s, ...をもっている。ここで２つの原子が近づくと、波動関数が重なり、２つの分子軌道に分かれる。そして、バンドギャップが生じる。バンドギャップは、別の言い方をすれば、２つの原子の結合力を表す。

一般にN個の原子が集まれば、N個の準位に分裂する。

準位はN個に分裂しているがエネルギー差が小さい。ほとんど連続的であり、これをエネルギーバンドと呼ぶ。

波動関数の重なりが小さいと、(孤立した原子の状況に近く）バンドの幅は狭い。これは内殻電子に相当する。一方、波動関数の重なりが大きいと、バンドの幅が広い。これは価電子（最外殻電子）に相当する。

（２）Bloch電子

結晶は周期性を有しており、その中にいる電子は周期的なポテンシャルを感じる。ポテンシャルは結晶と同じ並進対称性をもち、

と書ける。

周期ポテンシャル中を運動する電子の波動関数は、

と表せる（ブロッホの定理）。ここで、

である。結晶の周期性を反映した周期関数u_kに、平面波がくっついた形をしている（絵）。電子は各原子からの強いポテンシャルを感じても、平面波のような固有状態を保つ。一般に、k_1、k_2、k_3は整数でない。ブロッホの定理の証明は、ネットで容易に見つかる（例）。

ψ_k(r)はブロッホ関数と呼ばれる。その周期性については、

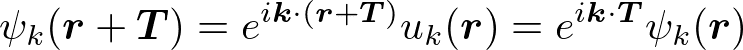
となり、波動関数は格子の周期をもたず、元の波動関数に位相因子をかけたものになる。逆格子の定義を思い出すと、kは逆格子ベクトルと同じ次元で同じ基本ベクトルをもち、逆格子空間に属するといえる。もしk_1、k_2、k_3が整数のときには、kは逆格子ベクトルに一致し、ブロッホ関数は周期的になる。

なお、ブロッホの定理は一般的なもので、電子系に限らず、周期的環境下における系の固有関数は必ずブロッホ関数でなければならない。

例として、一辺aの単純立方格子を考え、それぞれの方向にNaの周期境界条件を課す。つまり、

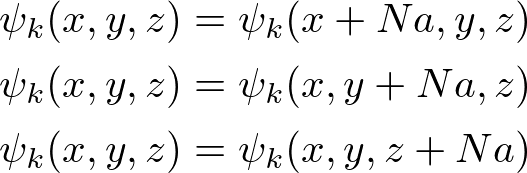
と書ける。基本並進ベクトルは、

であり、逆格子の基本並進ベクトルは、

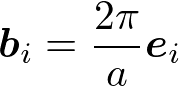
と書ける。さて、周期境界条件にブロッホ関数を代入して、

よって、

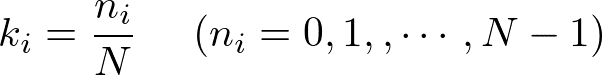
となる（Ｎ個）。第一ブリルアンゾーン内にとれば、

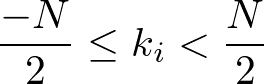
である。いずれにせよ、結晶運動量kは第一ブリルアンゾーン内にとることができ、バンドは逆格子の周期をもつ。第一ブリルアンゾーンという一周期分のエネルギー分散図を使うことができる。なお、今の場合、ｋベクトルは、

と書ける。第一ブリルアンゾーンの端のkは、k=±π/aである。

バンドギャップは、下図のように、k=nπ/a のところで生じる。この条件は、電子を波としてとらえたときのブラッグ反射条件（行路差=nλ）に相当する。

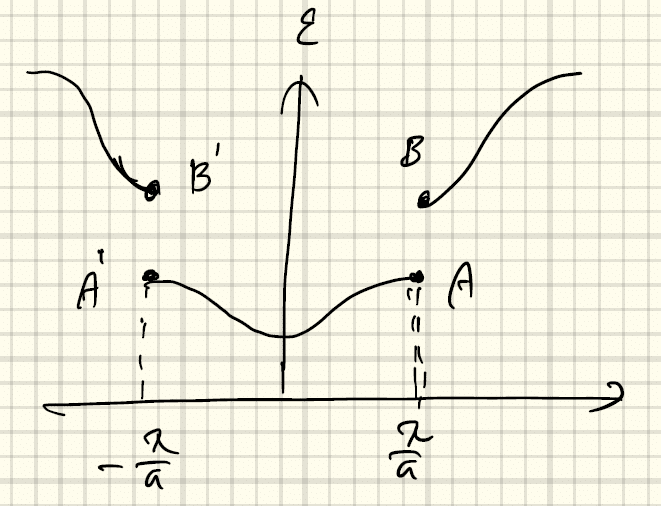
ｋの周期性から、点ＡとＡ’は同じ状態を表す。点Aのk=π/a=2π/2a より、右に進む波長2aの波と考えることができる。一方、このとき、以下のように、間隔aで並んでいる原子に対する反射を考えると、

行路差は2aであり、波長に一致する（ブラッグ条件を満たす）。このとき干渉の結果、強い反射波を作り、進行波と混ざることにより、静止した定常波が得られる。実際に上のバンド図で、点AとA'で、dε/dk=0（群速度0)となっている。このように行路差2aが波長の整数倍の時（k=nπ/aの時）に、強い干渉効果が起きて、ε(k)が不連続になる。

ブロッホ電子とエネルギーバンド

もう少し真面目に計算をしてみる。周期ポテンシャル中の電子のハミルトニアンは

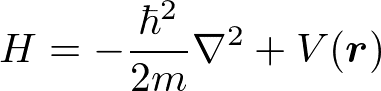
と書ける。ポテンシャルVは、前述のとおり、周期的である。シュレディンガー方程式

の解は、ブロッホの定理より

の形をとる。

u_k(r)とV(r)は周期的なので、フーリエ級数展開すると、

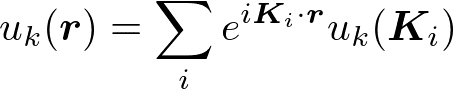
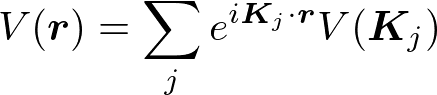
シュレディンガー方程式に代入して、

左から　

をかけて、rで積分すると

を得る。（級数をNで打ち切り）行列で書くと

のようになる。意味のある波動関数が得られるためには、このN×N行列の部分の行列式が０になる必要がある（永年方程式）。これを解くと、N個のE_kが求まることになる。これをバンド構造とよぶ。

（例）１次元の例：Kronig-Pennyのモデル

１次元の周期ポテンシャルを考える。

ポテンシャルの幅はb、周期はLである。電子のエネルギーEは、ポテンシャルの高さV_0より小さいとする。

シュレディンガー方程式を書き下すと、

・0≦x≦a で

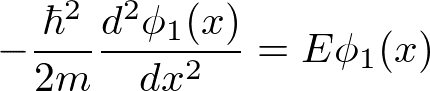
・-b≦x≦0 で

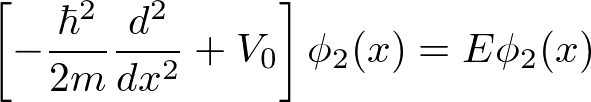
波動関数を求めると、

ここで、

である。A_1～B_2の係数は、接続条件から求まる。ブロッホの定理を使うことで、他の領域に波動関数を拡張でき、それを利用して接続条件の式をたてる。

・x=0での接続条件は、

・x=-bでの接続条件は、ブロッホの定理を使うと、以下のようにx=aでの接続条件を考えることになる。

ここで右辺においては、x=-bでの波動関数の値にe^ikLをかけている（ブロッホの定理）。

まとめると、

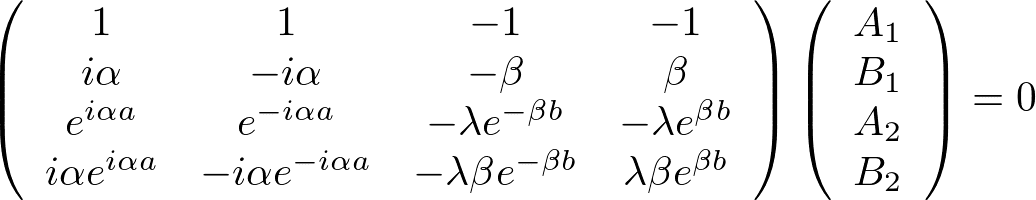
となる。ここで、

とおいた。A_1～B_2が意味ある値をとるには、この４×４行列の行列式が０でない必要がある（永年方程式）。永年方程式を解くと、

を得る。λが虚数を含んでいるが、

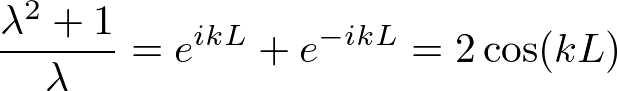
を使うと虚数は消えて、

を得る。αとβのなかにエネルギーEが入っていることを思い出すと、この式を解けば、k vs. Eのグラフが得られる。ポイントとしては、上式には三角関数が含まれているが、その大きさは１以下なので、それによりエネルギーEに制限が生じる。これがエネルギーギャップの存在につながってくる。

上式はこのままでは解けないので、以下のような極限を考える。

つまり、ポテンシャルの幅を狭くし、高さを無限にもっていく（その積は一定）。このとき、

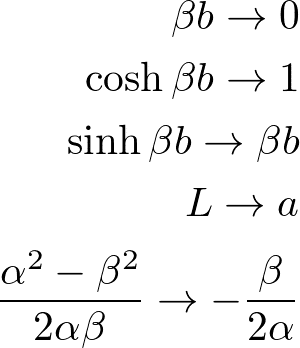
を使うと、

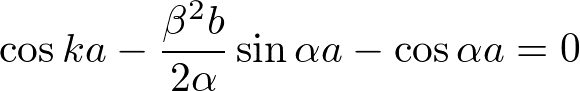
となり、さらに変形をしていくと

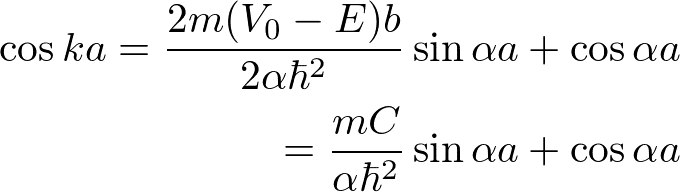
例えば、C=0（ポテンシャルの影響が全くない）のとき、

よって、

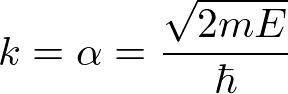
より

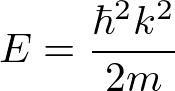
これは自由電子を表している。

一方、C＝∞のとき、

よって、

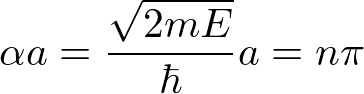
よって、

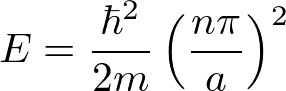
を得る。ポテンシャルの影響が強い極限においては、ｋによらずに離散的なエネルギーををとる。

通常は、C＝０とC=∞の中間の値をとる。その状況を図示すると

となり、エネルギーギャップが生じる。wikipediaやここなどに、きれいな図がある。

以下の２つの近似が、バンド構造を考えるときに用いられる。

・ほとんど自由な電子の近似（nearly free electron model)

まず、周期ポテンシャルが無視できる結晶格子（空格子）のとき、自由電子であるから、波動関数は平面波

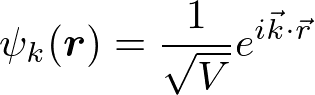
エネルギー

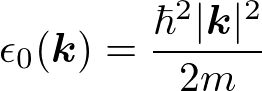
である。ただし、既に学んだように、kは離散的な値をとる。波数ベクトルkが逆格子ベクトルだけ異なるブロッホ関数は同一の状態を表すので、

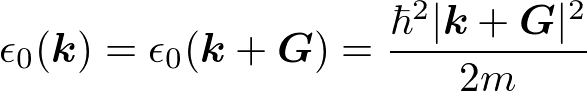
である。一次元の場合（格子定数a）に、この様子を図で表すと以下のようになる。エネルギーは周期的に振る舞うので、第一ブリルアンゾーン内で示せば十分である。

明らかに、空格子の場合にはエネルギーギャップは生じない。

続いて、弱い周期ポテンシャルを摂動として導入することを考える。

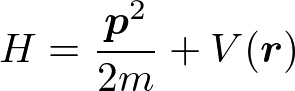
エネルギーは

と変更を受け、一次摂動項は

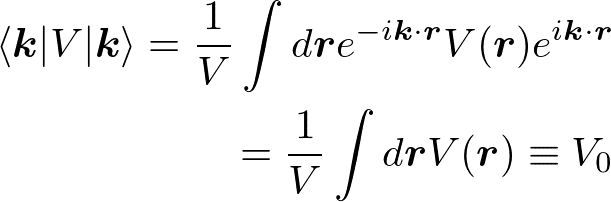
これは定数であり、全体として定数項のエネルギーシフトを表す。V_0=0とおくことが多いようである。二次の摂動項は、

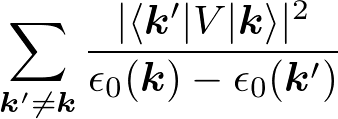
であるが、先ほど見たように、分母がゼロになる場合があり（＝ブリルアンゾーンの端）、発散してしまう。すなわち、縮退した場合の摂動論が必要になる。（上述の、一次の摂動の計算も見直すべきである。）

波動関数を、縮退した状態の線形結合

で書き、シュレディンガー方程式に代入する。

左から<k|をかけて積分すると、V_0=0として、

左から<k+G|をかけて積分すると、

ここで、

よって、

αとβが0でないためには、

ブリルアンゾーンの端にギャップが開くことがわかる。

この計算は、バンドギャップがブラッグの反射条件を満たすために生じるという直観的説明と対応する。上の式から、αとβは、

を満たす。式変形をさかのぼると、エネルギーが同じの波数kの状態と波数k+Gの状態を、同じ重みで線形結合した状態を波動関数として考えたわけである。これはブラッグ反射の考察に対応する。

・強結合近似（タイトバインディング）

内殻電子のように、原子核に強く束縛されている場合を考える。格子点R_mにある原子の、エネルギー準位ε_nに対応する電子の波動関数を

とおき、電子の波動関数を以下の線形結合で近似する（LCAO法）。

Ｎは単位胞の数である。係数の指数関数は、ブロッホの定理を満たすために現れた。波数kで指定されるブロッホ波になっていることは、以下のように示せる。

とおくと、u(r+T) = u(r)である。

強結合近似では、原子への束縛が強いため、電子の感じるポテンシャルは、R_mの近傍では

に等しく、その他の原子からの項

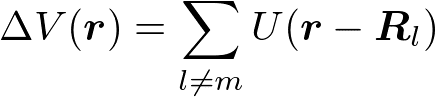
を小さいとして摂動にとる。エネルギー

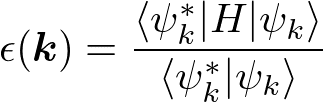
の分母は、

ここで、電子がR_mに局在しているので、m=lの項のみが主要として残した。よって、

となる。積分は、同じ原子位置（R_l = R_m)のとき（第一項）と、隣接した原子位置のとき（第二項）のときに大きな値をとるとする。それ以外の離れた原子位置での積分は、小さいとしてゼロにとる。結果として、

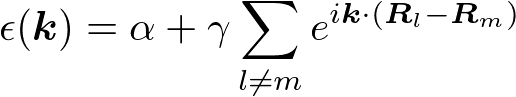
のように書ける。（記号や細かい表記は文献によって異なる。）和は、最近接のみに対してとる。例えば、一次元格子の場合（格子定数a)、

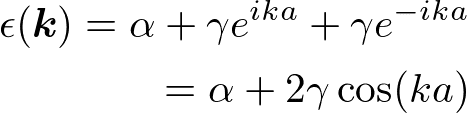
となる。絵に描くと以下のようになる。

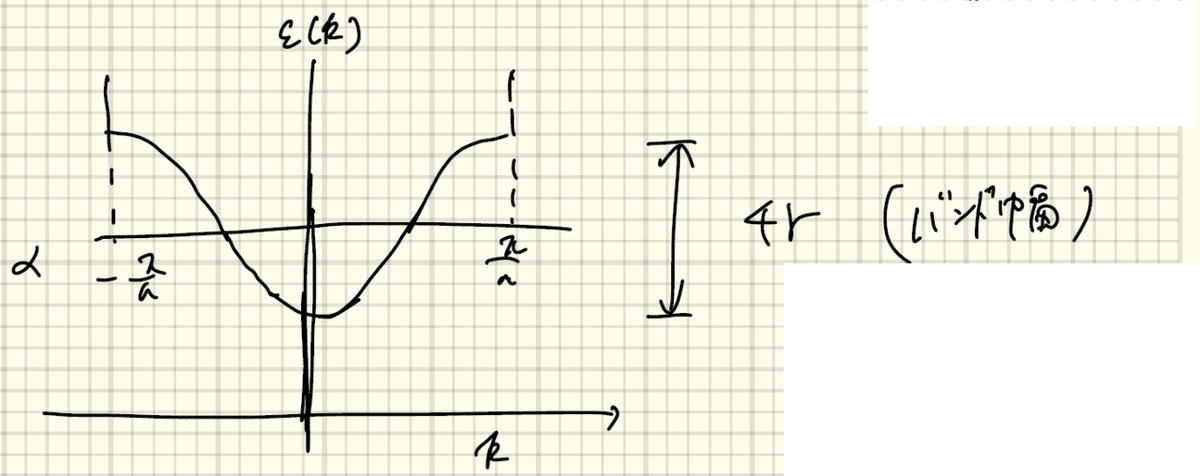
k=0付近で、~k^2となり、自由電子の場合と一致する。また、波動関数の重なりが大きいほど、γは大きくなる。例えば、遷移金属の場合、局在の大きい3dバンドのバンド幅は狭くなり、遍歴性の強い4sバンドはバンド幅が広くなる。

強結合近似で重要なことは、バンド指数の意味が明確なことである。nは、1s, 2s, 2pといった原子軌道に対応する。

（３）物質の分類（金属、半導体、絶縁体）

電気伝導度の違いによる物質の分類として、

・金属：よく電気をとおす

・絶縁体：電気を通さない

・半導体：中間の電気伝導度

が知られている。バンド理論の重要な成果は、金属と絶縁体の違いを説明したことにある。

まず、原子は電子をたくさんもっているが、内殻電子のバンドは、孤立原子に近い電子状態であり、バンドは完全に占有されている。この場合、（今から説明するように）電気は流れない。

一方、価電子のバンドは、完全に占有されたり、部分的にしか占有されなかったりする。価電子のバンドの状況で、電気伝導度に差が出る。

以下、一次元の系で簡単に考察する。§１で学んだことを思い出すと、長さがLの有限サイズの場合、ｋは離散的になる。長さ

として、

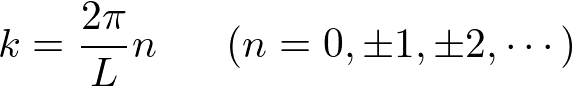
ここで、kは-π/aからπ/aの値をとり、ｎに換算すると、-N/2からN/2までに相当する。両端は同じ状態なので、ｋの状態の数はN個である。これは、結晶中の単位構造（原子）の数に相当する。ただし、スピンの上向き/下向きの自由度があるので、１つのバンドに収容できる電子の数は２N個になる。

①原子１個あたり２ｎ個（偶数個）の電子（結晶全体で２ｎN個の電子）をもつとし、バンドにつめていくとする。

低エネルギーの状態から順につめていくとすると、下からｎ番目まで完全につまる。n+1番目のバンドは空っぽである。バンドが完全に詰まっていると、電気は流さない（絶縁体）。

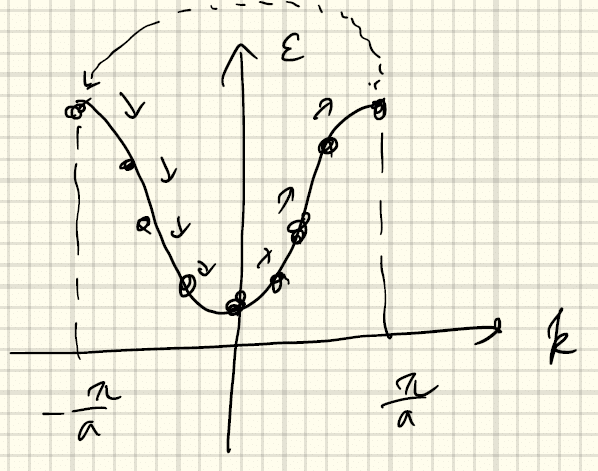
その理由は以下のとおりである。電場をかけたとき、運動方程式

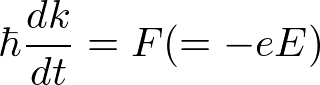
に従って、電子はｋ軸に沿って一方向に移動する（上図）。個々の電子のｋは変化するが、全体としては何も変化しない。つまり、電子の速度はdε/dk（接線の傾き）で与えられるが、k<0の領域では速度は負、k>0の領域では速度は正となっており、全体として平均速度は０である。

②次に、１原子あたりの電子数が奇数2n+1個のときを考える。このときは、全体として2nN+N個の電子がある。したがって、ｎ番目のバンドまでは満杯になり、n+1番目のバンドは下半分のみがつまることになる。このとき、系は金属になる。

これは先ほどと同様に、電場がかかったときのｋ軸上での電子の動きを考えると、今度は電子分布が左右でずれるからである。平均速度はゼロでなくなり、電流が流れる。

なお、実際の物質ではバンド構造はもっと複雑で、２つのバンドの重なり合いも起こり得る。２つのバンドが伝導に寄与する場合は、上記のような簡単な議論にはならない。

金属と絶縁体の分類については、『物性論』（黒沢達美）が丁寧である。