力学§３：運動の法則

§３．１　ニュートンの三法則

ニュートンの三法則とは以下の３つの法則である。

①第一法則：力を受けない質点は、静止あるいは等速直線運動を行う。（慣性の法則）

②第二法則：質点mの質点に力Fが作用すると、力の方向に加速度aが生じる。（運動方程式）

③第三法則：２つの物体があり、一方の物体Aがもう一方の物体Bに力Fを及ぼしている場合、物体Aは物体Bより力-Fを及ぼされる。（作用反作用の法則）

歴史的には、ニュートン以前の時代において、アリストテレスは力は速度に比例する(F=mvのような式)という考えだったようである。これは物体が運動しているなら力がはたらいているだろうという直感に由来すると思われるが、第一法則はこれを否定している。

ニュートンの三法則の一つの見方として、「力」に注目するものがある。すなわち、「力」というのは日常的な言葉でありいささか曖昧に用いる場合もあるが、物理学としての正確な定義が必要である。第一法則は、力というものが存在し、運動状態の変更に必要となるものを力と定義している。第二法則は力を定量的に表現しており、第三法則により力が物体同士の相互作用によって生じることがわかる。

別の見方をすると、第一法則は、慣性の法則が成り立つような座標系が存在することを主張しており、それを慣性系と呼ぶ。慣性系では、第二法則に規定される運動方程式が成り立つ。一方で、加速する座標系は非慣性系と呼ばれる。加速する電車の中に固定された座標系などがその例であり、生活の中でしばしば経験する状況であるが、我々のここでの主な興味はニュートンの三法則が成り立つ慣性系である。

問３．１　以下の図のように天秤が釣り合っている状況を考える。左側の栓を抜いたら水が下のタンクに落ちる。水が下のタンクに達しない間、天秤は左に傾くか、右に傾くか、釣り合ったままか[3]。

今後、質点の運動を考えるが、その基礎となるのは運動方程式（第二法則）である。はたらいている力がわかれば、それは位置ベクトルの時間に関する二階微分に比例するため、時間に関する積分操作を行うことで、質点の運動を求めることができる。

§３．２　次元と単位

次元とは、物理量からその大きさを除いた概念である。通常[F]のように[ ]括弧を用いて表す。基本的な量は、[r]=L（長さ）、[m]=M（質量）、[t]=T（時間）である。例えば、力については、質量×加速度なので

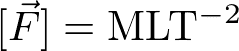
のように表せる。

次元を利用すると計算間違いに気付けるというメリットがある。すなわち、力を計算していて最終的な答えが上記の次元になっていなかったら間違った答えを出していることになる。

単位系は、様々な数量を計測するための尺度を規定するものであり、例えば長さであれば尺・寸のような単位も日本にはあった。しかし、物理学の議論には国際的に統一された単位を使うのが好ましく、時間の単位は「秒」、長さの単位は「メートル」、質量の単位は「キログラム」が通常用いられる。このとき、力の単位は、

となる。上記のN（ニュートン）のように、重要な組立単位は固有の名称を有する場合がある。

§３．３　基本的な力

①重力

自由落下の場合、鉛直方向をz軸（上向きを正）にとると、加速度は重力加速度gを用いて

であり、力は

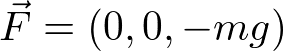
と書ける。以上より重力を感じて自由落下する質点の運動が求められる。速度ベクトルは、加速度を時間に対して積分することで得られる。

位置ベクトルは、もう一度時間で積分することで得られる。

位置が時間の関数として得られており、これが質点の運動を表している。質点の運動は質量によっておらず、物体は重さによらず同じように落ちることを意味する。アリストテレスは重いものほど速く落ちると主張していたようで、ガリレオにより否定されたとされる。ガリレオがピサの斜塔の上から実際に落下実験を行い実証したという話もある。なお、現実には、空気抵抗のない真空中ではこの法則は正しいが、空気抵抗を考えると修正が必要になる。

問３．２（放物運動）時刻t=0に、点r_0（位置ベクトル）から質点を速度ベクトルv_0で放出したとする。運動の軌跡を求めよ。

重力の原因に目を向けると、重力は物体と地球の間の万有引力で説明される。物体２（位置ベクトルr_2）が物体１（位置ベクトルr_1）から受ける万有引力は、万有引力定数をGとすると

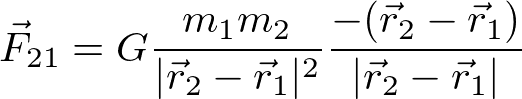
と書ける。長さが１の単位ベクトルをあらわに書く方式で表現している。ここで、物体１が物体２から受ける万有引力は大きさが同じで反対方向であり、

である。

今、質点が地球から受ける万有引力を考えるが、地表からの高さを無視して地球の半径で近似すると、地球の質量をM、物体の質量をmとして

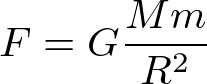
となる。ここで、向きは書いていないが、鉛直下向きに力がかかっている。ニュートンの第二法則（運動方程式）より、

であるから、両者を等しいと置くことで、

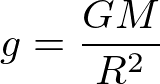
が得られる。ここで、重力に寄与する質量m（重力の原因となる質量：重力質量）と慣性質量m（加速度の係数：慣性質量）が等しいことは自明ではなく、重力質量と慣性質量とが等しいことを等価原理と呼ぶ。

②弾性力

弾性力は、簡単に言えば、ばねに働く力である。ばねにつながれた質点が伸びる/縮んだときに元に戻ろうとする力である。ばね定数をkとおいて、

である。l_0はもともとのばねの長さである。この法則をフックの法則と呼ぶ。

問３．３　ばねの運動

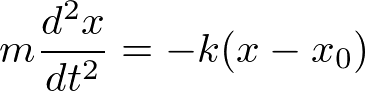
を解いて、x(t)を求めよ。

③摩擦力

摩擦力とは、固体表面が互いに接しているときに、それらの間にはたらく相対運動を妨げる力のことである。静止しているときの摩擦力を静止摩擦力といい、最大静止摩擦力は垂直抗力Nに比例することが知られている。

係数μを静止摩擦係数と呼ぶ。一方、動いているときの摩擦力を動摩擦力といい、この場合も近似的に同じ形の式で表現される。

問３．４　下図のように、道の上を走る車を考える。車は右方向に加速しているとする。このとき、車には重力と垂直抗力と摩擦力がはたらいている。（１）この摩擦力は、（あ）動摩擦力か（い）静止摩擦力か。また、（２）摩擦力の方向は（あ）進行方向か（い）進行方向とは逆か[3]。

§３．４　運動量と力積（保存則①運動量保存則）

運動方程式

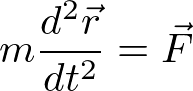
は、位置ベクトルの時間に関する二階微分が入った方程式である。したがって運動を予測するには積分操作が２回必要となる。しかし、保存則を適切に用いると、より簡単に運動を予測することができる。

運動方程式を時間に関して積分することを考える。まず左辺の積分は、

となる。ここで、pは運動量ベクトルであり、カッコ内は時刻を表している。よって、全体で

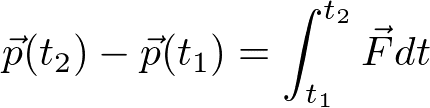
が得られる。右辺は力積と呼ばれる量である。特に重要な場合は力積がゼロになるような場合であり、運動量が保存する（運動量保存則）。いくつかのポイントを以下にまとめる。

①力がはたらかない（合力がゼロの）質点の運動量は時間変化しない（運動量保存則）。この性質は、例えば、多粒子が衝突する場合（２つの球がぶつかって跳ね返るとか）に重要である。衝突前の全運動量と衝突後の全運動量が保存しており、（１）１つずつの粒子の運動を考えなくてよい、（２）衝突の途中経過を考えなくてよい、というメリットがある。

②力が時間の関数として与えられれば、運動量の変化がわかる。

③力が一定の方向を向いていれば、その方向に垂直な方向の運動量の成分は保存する。

教科書によくある例は、バットでボールを打つ場合である。（このような短時間のみ継続する力を撃力と呼ぶ。）力の時間変化は複雑でわからないが、力積はボールの運動量の変化で与えられるため、衝突前後のボールの運動量を計測すれば、バットにより加えられた力についてある程度情報を得ることができる。また、スポーツとしては、大きい力を短い時間与えることと、小さい力を長い時間与えることは同じ効果であることがわかる。

§３．５　力のモーメント（保存則②：角運動量保存則）

運動方程式の左から、位置ベクトルをかけて外積をとると、

となる。次にこの式を時間積分する。左辺は、

となる。ここで、部分積分を行った。角運動量ベクトルを

と定義すると、全体で

が得られる。右辺の被積分項

は力のモーメントと呼ばれる。（一般に、r×A をAのモーメントと呼ぶ。）この式より、角運動量は力のモーメントが加わることで変化することがわかる。特に重要な場合として、力のモーメントがゼロならば角運動量は保存する（角運動量保存則）。

力のモーメントは、＋ドライバーを例として考えるとわかりやすい。先端が細い1mm径の＋ドライバーと太い1cm径の＋ドライバーでは、単純には、（同じ力に対して）１０倍の力のモーメントの差がある。

角運動量が保存する場合として、月の公転（万有引力）がある。月が地球の周りをまわるとき、力は公転軌道の動径方向を向くから、rとFは平行であり、力のモーメントはゼロになる。したがって、角運動量は保存する。

別の例として、ドローンがある。ドローンの羽は４枚あるが、羽は対角の２枚が右回り、別の対角が左回りの回転を行うようになっており、全体として角運動量がゼロになるようになっている。そうしないと、ドローンが動き始めたときに、もともとゼロだった全角運動量を保存するために、ドローン自体が回転してしまうためである。（意図的にドローンを回転させたい場合は、右回りと左回りの羽の回転数を調整する。）

問３．４　xy面内を運動する質点の角運動量ベクトルは、ｚ成分のみゼロでない値をとる。角運動量のｚ成分をxy面内の極座標で表せ。

§３．６　仕事とエネルギー

運動方程式に対して、速度ベクトルの内積をとると、

となる。次に時間に対して積分をとる。上記の左辺が

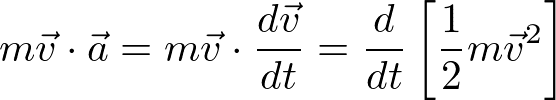
であることに注意すると、積分の結果は

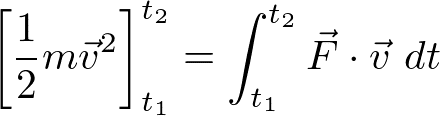
となる。左辺は運動エネルギー(Kと表す）であり、右辺を変形すると

が得られる。式変形の途中で時間に関する積分を線積分に書き換えた。Wはrの経路に依存する積分量であり、仕事と呼ぶ。この式は、運動エネルギーの変化は与えられた仕事に等しいことを意味する。

仕事という言葉は日常でも用いられるが、意味は大きく異なる。例えば、物を押したとき、力を加えて物が動かなかった場合は仕事はゼロである（が我々は疲れるので仕事をした気分になる）。また、力を加えた方向と物体の運動が逆向きであれば仕事は負になる。

先にも考えた月の公転においては、力が中心方向（地球の方向）を向き、公転経路と直交しているので、仕事はゼロになる。力が仕事をしなければ、速さは変化しないとも言える。

§３．７　保存力とポテンシャルエネルギー

質点が点Aから点Bまで経路Cに沿って運動するとき、仕事は

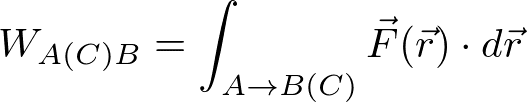
と書ける。別の経路C'でAからBまで運動するときは、

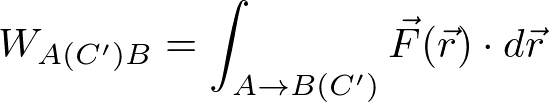
である。経路によらずに仕事が等しい（仕事が始点と終点のみで決まる）とき、Fを保存力とよぶ。保存力については、

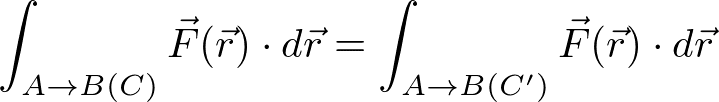
と変形することができる。この式は、Aから経路Cを通ってBに行き、その後BからAに経路C'を逆向きにたどって戻る経路の積分をとると、ゼロになることを意味する。このような閉じた経路についての積分（周回積分）を

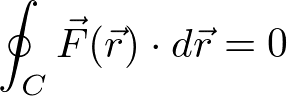
のように表現する。

力Fが保存力の時、

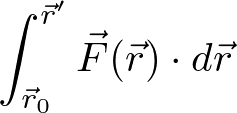
は経路によらず、始点r_0と終点r'の関数である。

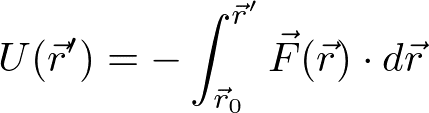
をr_0を基準にしたときのポテンシャルエネルギー（位置エネルギー）と呼ぶ。

例として重力を考える。鉛直方向をｚ軸にとると、

であり、ある経路Cに対して仕事は、

となる。結局、AとBのｚ座標だけで経路によらず仕事が決まっており、重力は保存力であることがわかる。また、ポテンシャルエネルギーは、

となり、mg×(高さ)という見慣れた形となる。

保存力であるのは、重力のほかに、クーロン力やばねの弾性力があげられる。一方、保存力でないのは、摩擦力や抵抗力であり、

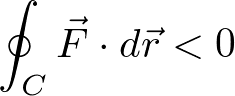
の関係がある。

問３．５　一次元ばねの弾性力

に対するポテンシャルエネルギーを求めよ。

§３．８　力学的エネルギーの保存則（保存則③：エネルギー保存則）

保存力だけを受けて運動するとき、

と表せるので、運動エネルギーの変化が仕事に等しいという式から

が得られる。移項すると

となり、力学的エネルギー（運動エネルギーとポテンシャルエネルギーの和）が保存することを示している。すなわち、保存力のみを受けながら運動している物体の運動においては、力学的エネルギーは一定である。

例：重力の場合、

であったから、力学的エネルギー

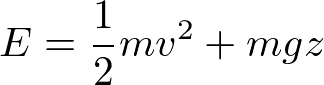
が保存する。