『物性物理学１』§２：物質の構造

（１）結晶の構造～周期性と並進対称性～

格子は周期的なのであった。

それぞれの格子点をベクトルで表すと、二次元のときは

３次元のときは

と書ける。a_1, a_2, a_3ベクトルを基本並進ベクトルと呼ぶ。n_1, n_2, n_3は整数である。上図に二次元の例を示す。格子点は周期的に並んでいるので、基本並進ベクトルの重ね合わせで書くことができる。重要なこととして、基本並進ベクトルのとり方は一意ではない。一番使いやすい（対称性がよい）とり方をするのが普通である。

もう少し複雑な例（現実の物質に近い例）を以下に示す。今まで単純化してきたこととして、格子点に原子があるわけではないということである。格子は枠にすぎない。

まず、Aという原子とBという原子は、周囲の環境が異なるという意味で、等価でなはい。このAとBから成る基本構造を、並進対称操作により再現できる格子にのせると、結晶構造が得られる。この場合は、基本構造を１つの点とみなして（格子点）、その配列を考えることになる。

格子点を見つけるポイントは、あらゆる格子点は等価である、ということである。周囲の環境が同じと言い換えることができる。

対称性という観点で重要なこととして、格子には「並進対称性」がある。並進対称操作は

で与えられる。m_1, m_2, m_3は整数である。格子点の表現式から明らかなように、格子は並進対称性をもつ。

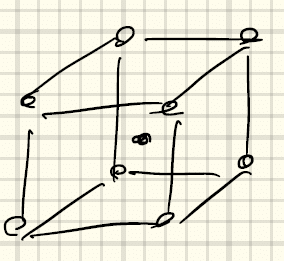
格子の周期性の最小単位を、「単位胞」（unit cell, 単位格子）と呼ぶ。下に図示した格子の絵を見ると、３つの基本並進ベクトルa_1, a_2, a_3によってできる平行六面体が単位胞になることがわかる。

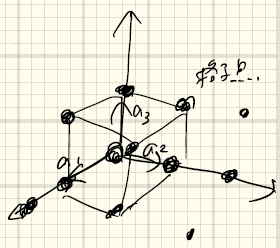
基本並進ベクトルのとり方が一意ではなかったように、単位胞の選び方は１つではないことに注意する。その中で特に重要となる単位胞が、「Wigner-Seitz cell」 (ウィグナー-ザイツ単位胞)である。Wigner-Seitz cellを得る方法は以下の通りである。

①１つの格子点を原点にとる

②隣接する格子点を結ぶ垂直二等分線を描く

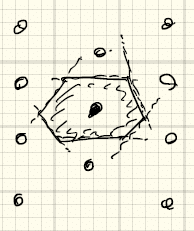
Wigner-Seitz cellは格子点を１つだけ含んでおり、他の単位胞と同様に並進対称操作で全空間を埋め尽くせる。

単位胞は時に単位格子とも呼ばれるが、意味するところは少し異なるようだ。例えば、上の図は、格子点を結んだ図形ではないので、（単位胞ではあるが）単位格子を呼ぶべきではないということである。

単位胞の取り方が複数あることを見るために、例をネットで探してみる。二次元の場合は、例えば、ここにある。単位胞の複数の取り方が説明されている。

三次元の場合では、面心立方格子の例がここにある。面心立方格子は、立方体の頂点と、各面の中心に原子がある。高校的な考えでは、立方体を「格子」と考えて、４個の原子が「基本構造」であると考える。しかし、ここに説明されるように、４個の原子は周囲の環境が同じであり、区別するべきではない。ここの右図で示すように、単位胞に一つの格子点だけが含まれるように単位胞をとることが可能である。このように単位胞に一つの格子点だけ含まれるとき、プリミティブ（単純）単位胞と呼ぶ。

対称性の観点から重要なこととして、格子には「回転対称性」がある。つまり、並進対称性に加えて、回転対称性を有する。ただ、格子点は離散的であるので、許される回転角は限定される。イメージとして例えば、２５°の回転を考えると、

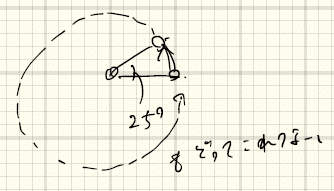
ぐるっと回って元に戻ってこれず、許されないことがわかる。実際に許される回転角は、60°、90°、120°、180°、360°である。n回回転対称性という表現では、それぞれ6回回転対称性、4回回転対称性、3回回転対称性、2回回転対称性、1回回転対称性、である。

以上のことから、実際の結晶の構造を思い浮かべたとき、格子定数a、b、c（基本並進ベクトルの長さ）と結晶の軸角α、β、γには制限があることがわかる。今からみるように、結晶格子は７つの結晶系と１４個のブラベー格子に分類される。このあたりは絵で見たほうがわかりやすいし、ネットで調べればすぐ出てくる。

まず、回転軸の種類と数によって、７種類の結晶系に分けられる。結晶系は対称性による単位格子の分類と思うことができる。それぞれwikipedia等で絵で見て確認すること。

①三斜晶（triclinic） 回転軸なし　：a ≠ b ≠ cかつα ≠ β ≠ γ

②単斜晶（monoclinic） １つの２回回転軸　：a ≠ b ≠ cかつα = γ=90°  β≠90°

③直方晶（orthorhombic） 互いに直交した３つの２回回転軸　：a ≠ b ≠ cかつα = β = γ =90° 

④正方晶（tetragonal）　１つの４回回転軸　：a = b ≠ cかつα = β = γ =90° 

⑤三方晶（trigonal）or 菱面体晶（rhombohedral）１つの３回回転軸　：a=b=cかつα = β = γ<120°, ≠ 90°

⑥六方晶（hexagonal）　１つの６回回転軸　：a＝b≠cかつα＝β＝90゜γ＝120゜

⑦立方晶（cubic）　４つの３回回転軸　：a=b=cかつα = β = γ = 90°

このように平行六面体がどのような回転対称性をもつのか、格子定数は辺同士で同じか、軸角がいくつか、という情報で結晶格子が７種類に分類される。

この７個の単純（プリミティブ）単位格子の中の適当な位置（例えば格子の中心とか）に新たに格子点を付け加えても、新しい格子を作る場合がある。ブラベーが、１４種類あってそれ以上ないことを証明したことから、ブラベー格子と呼ばれる。

ブラベー格子は、並進対称性も考慮した格子の分類と見なせる。上の７つの結晶系に属する計７つの単純（プリミティブ）単位格子は、格子点を１つしか含まない。単純単位格子は一辺の長さをずらすと重なることから、一辺分の並進対称性を有する。ここで、例えば、立方晶の面の中心に格子点があるとすると、例えば(1/2,1/2,0)だけずらす並進対称性が生まれる。これは元々なかった並進対称性であり、別の格子と考えられる。格子点を付け加える位置は、底心・面心・体心の３パターンである。これ以外の場所は、格子点は周囲の環境が同じという前提を満たさない。7 (対称性) × 4 (単純・底心・面心・体心) 種類のうち、重複を省くと１４種類になる。

１４個のブラベー格子のそれぞれについては、『物質の対称性と群論』（今野豊彦）が詳しい。以下では簡単に確認する。

以下の①～③は、以下の「オブリークネット」を積み重ねて得られる。

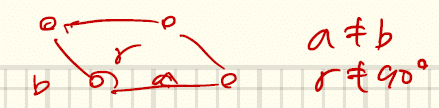
①三斜格子(triclinic)  a ≠ b ≠ cかつα ≠ β ≠ γ

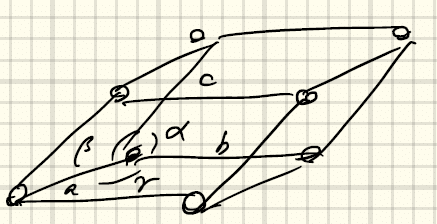
オブリークネットをずらして重ねた感じ。

②単純単斜格子（primitive monoclinic） a ≠ b ≠ cかつα = β = 90° < γ

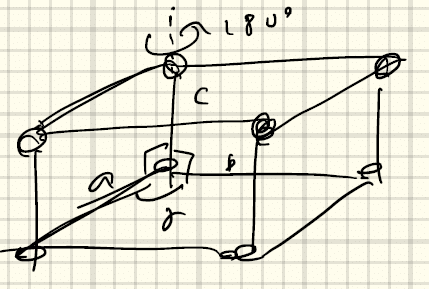
オブリークネットを真上に積み重ねた場合。二回回転軸が生まれる。

③側心単斜格子（side-centered monoclinic） a ≠ b ≠ cかつα = β = 90° < γ

側面の中心に向かってずらして重ねる場合。二回回転軸がある。

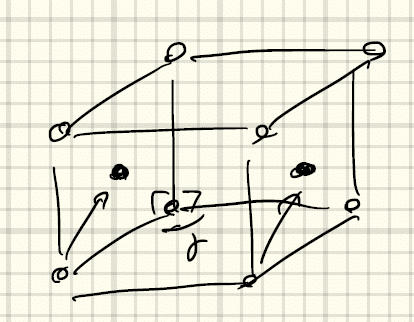
以下の④～⑥は、以下の「長方形ネット」を積み重ねて得られる。

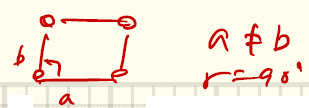
④単純直方格子（primitive orthorhombic）a ≠ b ≠ cかつα = β = γ = 90°

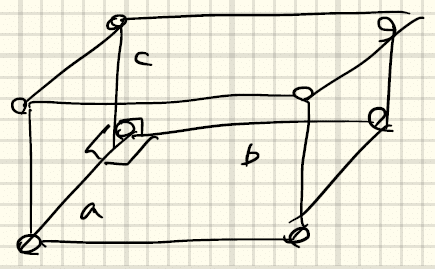
真上に長方形ネットを重ねた場合。

⑤側心直方格子（side-centered orthorhombic）a ≠ b ≠ cかつα = β = γ = 90°

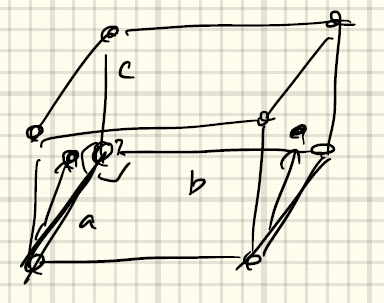
側面の中心に向かってずらして重ねる場合。

⑥体心直方格子（body-centered orthorhombic）a ≠ b ≠ cかつα = β = γ = 90°

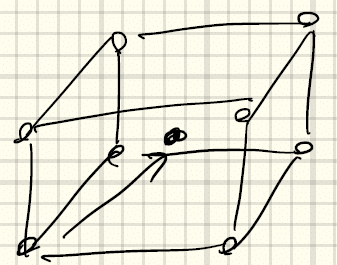
直方体の中心に向かってずらして重ねる場合。

　⑦は以下の「菱型ネット」をずらして重ねると得られる。

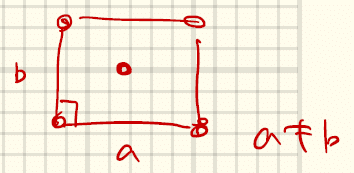
⑦面心直方格子（face-centered orthorhombic）a ≠ b ≠ cかつα = β = γ = 90°

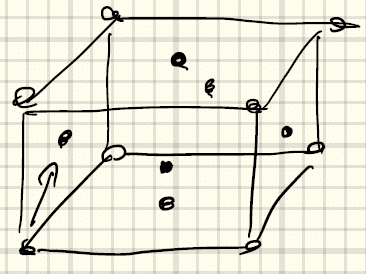
側面の中心に向かってずらして重ねる場合。

　以下の⑧と⑨は「正方形ネット」を重ねると得られる。

⑧単純正方格子（primitive tetragonal）a = b ≠ cかつα = β = γ = 90°

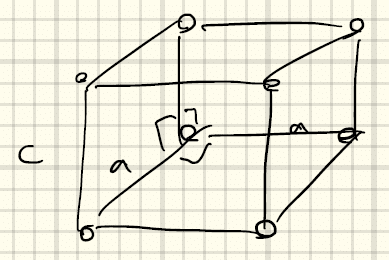
真上に重ねた場合。

⑨体心正方格子（body-centered tetragonal）a = b ≠ cかつα = β = γ = 90°

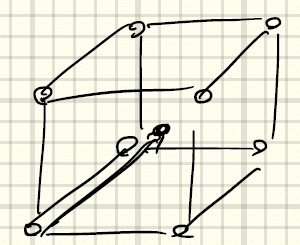
直方体の中心に向かってずらして重ねる場合。

　以下の⑩～⑭は、「六方ネット」を重ねると得られる。

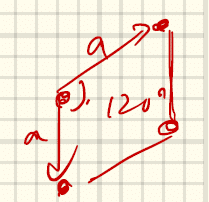
⑩六方格子（hexagonal）a = a ≠ cかつγ = 120°

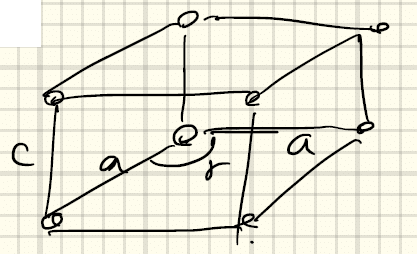
真上に重ねる場合。６回回転対称性が失われない。

⑪菱面体格子（rhombohedral）a = a = aかつα = β = γ ≠ 60°、90°、109.47°

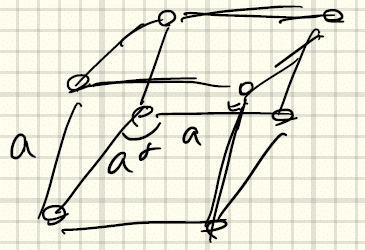
ずらして重ねていくと菱面体格子ができる。これはちょっと説明が難しいので教科書を見てほしい。

⑫単純立方格子（simple cubic）a = a = aかつα = β = γ = 90°

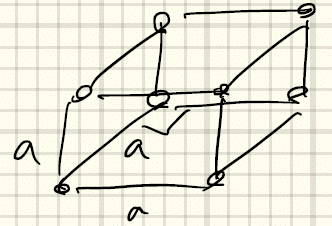
c=aで、γ＝90°の場合には、単純立方格子になる。

⑬面心立方格子（face-centered cubic）a = a = aかつα = β = γ = 90°

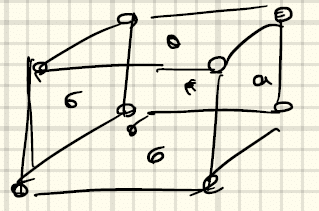
c=aで、γ＝60°の場合には、面心立方格子になる。

⑭体心立方格子（body-centered cubic）a = a = aかつα = β = γ = 90°

c=aで、γ＝109.47°の場合には、面心立方格子になる。

結晶系とブラベー格子の関係は、wikipediaを参照のこと。

（２）結晶構造の判定法

逆格子

格子は周期的であり

と書けるのだった。格子をフーリエ変換したものを「逆格子」と呼ぶ。

逆格子Gの定義は、

となる点Gの集合である。答えを言ってしまうと、

と書くとき（m_1, m_2, m_3は整数）、

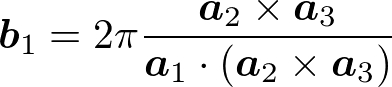
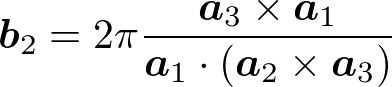
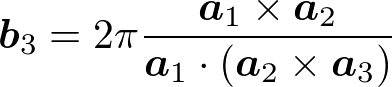
と表せる。実際、外積の性質により

となるので、

を満たすことがわかる。

例として、体心立方格子を考える。基本並進ベクトルは

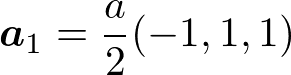
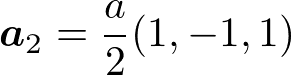
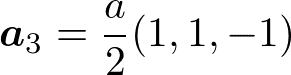
である。b_1, b_2, b_3の定義式に代入して、内積と外積の計算を頑張ると、

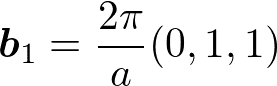
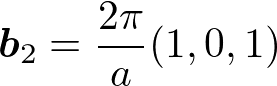
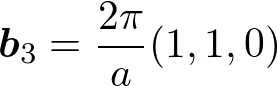
これは一辺4π/aの面心立方格子を表している。このように体心立方格子の逆格子は面心立方格子である。

ここで、逆格子が格子のフーリエ変換になっていることを確認しよう。簡単のため、一次元を考える。格子点は

である。密度ρは、

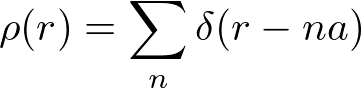
と書ける。フーリエ変換すると、

ディリクレ核の極限公式

を使うと、

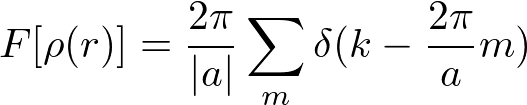
よって、k=(2π/a)mの格子になっている。一方、

からは、

より

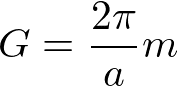
を得る。これはフーリエ変換した結果と一致している。

ブリルアンゾーン

逆格子空間のWigner-Seitz cellを「ブリルアンゾーン」と呼ぶ。ブリルアンゾーンはWigner-Seitz cellと同様の方法で得ることができる。つまり、隣接するすべての逆格子点への線分を引き、それらを垂直二等分する平面で囲まれた多面体がブリルアンゾーンである。（ブリルアンゾーンは重要な概念で、また後で出てくる。）

結晶格子の方位と面：ミラー指数

格子点

は、当然であるが、(n_1, n_2, n_3)の組で指定できる。これを[ ]括弧で表す。例えば、[1,1,1]のように表す。

一方、格子面を指定するには、格子点３つの座標を使えば指定できる。しかしながらそれは複雑である。そこで、結晶軸と交わる３点を使って、

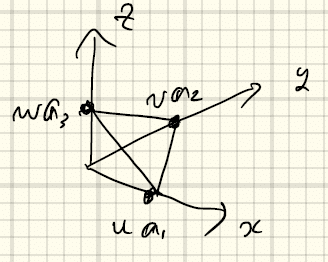
(u,v,w)と指定することを考える。一見これでよさそうだが、

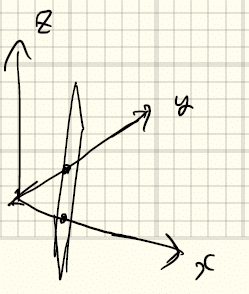
のように、軸に平行な面は(u,v,w)では指定できない。そこで、結晶格子の面の指定は

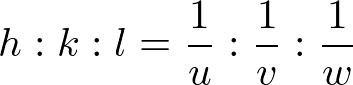
と逆数で指定する。面の場合は、(h,k,l)と ( )括弧で表す。

注意としては、通常は最小の整数に約分されたものを用いる。つまり、(2,2,4)は(1,1,2)と表す。また、負の数は上付きバーで表す。

 さて、(h,k,l)において、逆数をとったことが実は意味をもつ。一個前の図に戻ると、格子点

に対して、

は逆格子ベクトルになっている。なぜならば、

を満たすからである。

具体例として、(001)面を考える。

対応する(h,k,l)=(0,0,1)なので、

である。格子面上の点rとの内積は、

となっている。格子面の間隔dは、隣接する格子面の点r_1とr_2に対して

となることに注目すると、

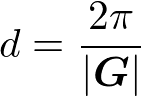
と書ける。正確には、

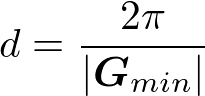
ここで、

は逆格子ベクトルの最小の長さである。

ブラッグの法則

結晶構造の詳細を調べるためには、X線、電子線、中性子線の回折を利用する。

上図より、

のときに干渉して強め合うことになる（ブラッグ条件）。ここで、λは波長である。実験的には、入射角度θを動かしていくと、上式を満たすθで回折線が得られることを利用する。

ここで、波長について制限があることに注意する。なぜなら

より、

となる。面間隔ｄ~Åなので、λはÅ程度に短くないといけないことになる。一方、λが短すぎたら、θが小さくなりすぎるので、実験が困難になる。ということで、ちょうどよい大きさの波長が必要である。よく使われるCu Kα線の波長は、λ=1.54 Åである。

なお、X線の波長とエネルギーの関係は

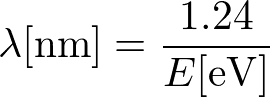
電子線においては

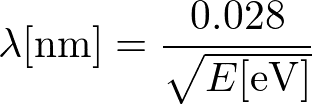
中性子線においては

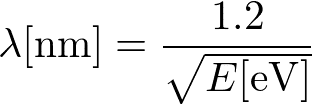
であり、同じ波長の波でも、エネルギーが異なる。その他、軽い元素への感度の違いや磁性への感度などに違いがあり、状況によって使い分けられている。

この方法を粉末試料（＝結晶面がランダムに向いている状態）に利用すると、多くの回折ピークが得られることになる。

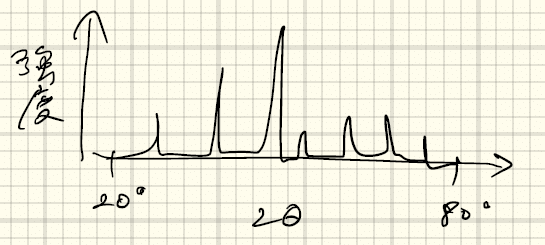
このピーク位置や強度は物質に固有であり、回折パターンから物質を特定することができる。これまでの導出を見ると、格子点、格子面で回折条件が定まるので、同じ格子をもつ物質であれば、同じような2θの位置に回折線が見られることになる。格子内の原子位置を決めている基本構造は、後で述べるように、構造因子を通じて回折線の強度に関係する。

ラウエ条件とブラッグ条件の等価性

試料をポテンシャルVとしてとらえ、フェルミの黄金律を適用すると、波数ｋの波がポテンシャルVに散乱されて波数k'になる遷移確率は

で与えられる。ここで、入射波と散乱波が平面波だと仮定すると

ここで、

（R: 格子ベクトル、x:単位胞内の位置）とおく。ポテンシャルVは、周期的

なので、

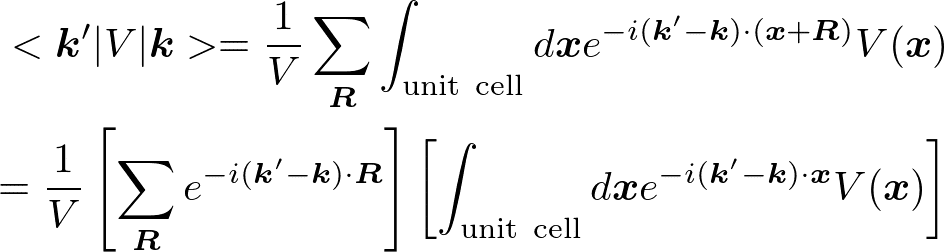
を得る。２つの[ ]の掛け算に分離でき、最初の[ ]は

のときのみゼロでない。これをラウエ条件と呼ぶ。これは（結晶）運動量の保存則に他ならない。また、フェルミの黄金律のデルタ関数の部分から、エネルギー保存則

も成り立つ。ラウエ条件が成り立つとき、

となる。積分項

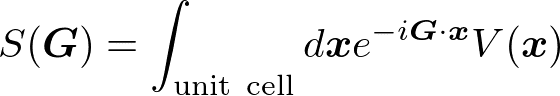
は構造因子と呼ばれ、散乱強度Iは、

と構造因子に依存する。

ラウエ条件とブラッグ条件は等価である。これは以下のように示すことができる。

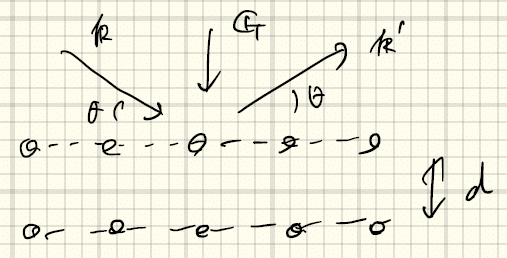
前提として、ラウエ条件

(上図のGのとり方でベクトルの差を考えると、k'-k=Gではなくk-k'=Gとなることに注意。)エネルギー保存

を仮定する。波数ｋは、波長に反比例し、

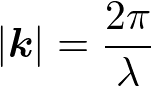
が成り立つ。また、前述のとおり、格子間隔ｄとGは

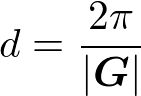
という関係がある。図を見ると、sinθは

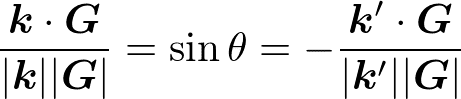
のように表すことができる。以上のことから、ブラッグ条件を導く。実際、

となり、ブラッグ条件が導かれた。

消滅則

結晶の対称性が高い場合には、回折線が消失することがある。例として、体心立方格子を考える。単位胞内の原子の位置は、x=(0, 0, 0), (1/2, 1/2, 1/2)なので、構造因子は

と計算できる。ここで、単位胞内の２つの位置に同一元素があるとして、同じVの値をもつと仮定した。この式より、m_1 + m_2 +m_3 =奇数のときに、回折線は消える。例えば、(1,0,0)、(3,0,0)、(1,1,1)は見えない。一方、足して偶数になる(2,0,0)、(1,1,0)、(2,2,2)は見える。なお、同一元素で構成されない場合は、回折線は弱めあうが、消えない。先述のとおり、基本構造は回折線の強度に強い影響を与える。

（３）点群と空間群

結晶の対称性をより数学的に表すことを考える。まず強調したいのは、対称性は物性の理解に重要であることである。例えば、結晶が（正方形のように）ｘ方向とｙ方向が等価ならば、電気抵抗もｘ方向とｙ方向で同じになるはずである。

ノイマンの原理：結晶のどの物性も、対称性は少なくともその結晶のもつ点群の対称性をもたないといけない。

「点群」の意味は今から説明する。ノイマンの原理は、平たく言えば、

　　　　　　物性の対称性　≧　結晶の対称性

である。原理なので証明はできない。さて、点群とは、

点群：１点（不動の点）のまわりの対称操作（＝点対称操作）の集合

である。点対称操作の例を以下にしめす。

①回転操作：　360°/n回転（n回の回転操作）　C_nと表記する。(C_1, C_2, C_3, C_4, C_6)

②鏡映操作：　鏡による反転　mやσで表す。

③反転操作：　１点について反転　iで表す。

④回反操作：　回転してから反転　n(1,2,3,4,6)に上付きバーをつけて表す。

いちいち文字で操作を表現するのは煩わしいので、記号を使って表す。

これらの対称要素が組み合わさって、全体として構造ができあがる。例えば、アンモニア分子NH3の場合は、３回回転軸に加えて、回転軸を含む鏡映面が存在している。これを「3m」と表現する。「３」が３回回転、「ｍ」が回転軸を含む鏡映面があることを意味する。

このように整理していくと、並進対称操作と両立する点群は３２種類しかないことが知られている。３２種類をすべて列挙するのは避けるが、ネットに多くの記事がある（例）。物性として重要な視点としては、中心対称性をもつか、もたないか、という点である。

・中心対称性をもつ点群（反転中心をもつ点群）　１１個

・中心対称性をもたない点群　２１個　そのうち、

　　　・極性をもつ点群　１０個

　　　・極性をもたない点群　１１個

中心対称性を持たない点群２１個のうち、１個を除いて、２０個の点群の結晶は「圧電性」を有する。圧電性があると、外部から応力を加えると電気分極が生じる。また、極性をもつ点群に属する結晶は、外部電場がゼロでも電気分極をもつ（「焦電性」、「強誘電性」）。対称性の破れがこれらの現象の発現に必要なことは、例えばここにイメージ図がある。中心対称性を持たない結晶構造の例は、例えば、MnSiなどのB20化合物がある。

点群で考えたのは、対称操作の結果、自分自身に戻ってくるかどうかの追求であった。だが、結晶は周期的なので、対称操作をしたときに自分自身に戻らなくてもよく、となりの単位胞の同一位置に戻ってもよい。このように、（点群と違って）「空間群」を考えるときは、並進操作が許される。

並進操作を許すことで新たに現れる対称操作は２つある。

①らせん操作：

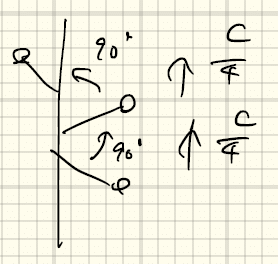
例えば、上図の例では、９０°回転＋c/4だけ移動 を４回繰り返して、となりの単位胞の自分自身の位置に戻るという操作である。これを4_1と表す（１は下付き文字）。

②グライド操作：　鏡映操作をした後に1/2の並進を行う。二回繰り返せば、隣の単位胞の自分自身の位置に戻る。a, b, c, n ,dなどの記号がある。

空間群は２３０個あることが知られている。例えば、ここに全部載っている。

点群や空間群は、『物質の対称性と群論』に詳しい。