『物性物理学１』§４：格子振動（フォノン）

（１）結合振動子モデルと周期性

結晶中において原子は周期的に並んでおり、原子は平衡位置周りに熱振動する。周期性より、ブロッホの定理を満たす（ブロッホ電子との類似性）。

①古典論

簡単な格子のモデルとして、同じ原子が一次元的に並んだ系を考える。それぞれの原子は、ばね定数ｋののばねでつながっている。原子間の間隔はaである。

ｎ番目の原子の運動

が、ばねとして振動が伝わっていく。以下で運動方程式を導く。

全ポテンシャルは、

と書けるので、ｎ番目の原子にはたらく力は、x_nで微分すると得られる。

よって、ｎ番目の原子のニュートンの運動方程式は

と書ける。解として、

を仮定して代入すると、（ばね定数ｋと波数ｋの区別に注意ください）

整理すると、

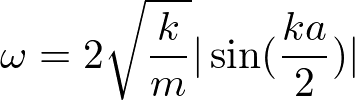
これを分散関係という。k - ωをプロットすると、

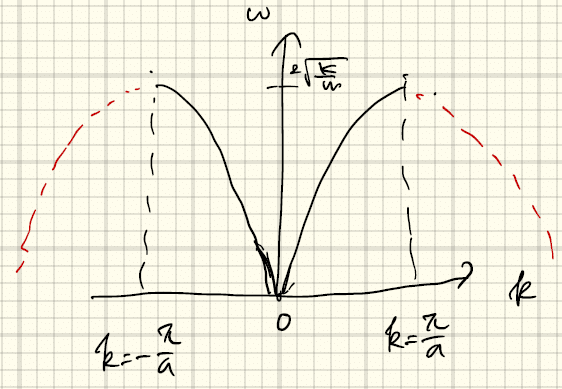
となる。いくつか重要な性質がある。まず第一に、ωに上限があることである。また、ｋ方向について、左右対称である（右に進む波と左に進む波のエネルギーが等しい）。ｋ～０（長波長極限）で、

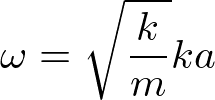
と線形に立ち上がる。さらに、

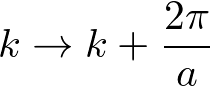
で周期的である。-π/aからπ/aの一周期の範囲が意味をもつ。

このような周期性は、電子系を考えたときにもみられた。一般に、実空間で周期的（周期a）な系は、逆格子空間（k空間）では周期2π/aで周期的であることが知られている。

ｋ空間での周期の単位（単位胞）をブリルアンゾーンと呼ぶ。k=0を中心とするブリルアンゾーンを第一ブリルアンゾーンという。k=0と等価な点k=(2π/a)nの集まりが逆格子である。

②量子論

上で考えた古典的な調和振動子を量子化すると、エネルギー固有値は

となる。フォノンは、離散的な量子振動である（結晶内に広がった波のエネルギーの量子化）。ωはkに依存し、先ほど古典論で求めた分散関係を用いることができる。各格子波は相互作用がなく、ぶつかっても互いに無関係に行違う。フォノンの運動量は、結晶運動量kを用いて

である。

フォノンはボーズ粒子であり、以下のボーズ分布に従う。

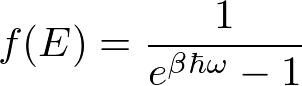
このような量子力学的な取扱いは、次節の比熱のところで詳しく取り上げる。

次に、（より現実に近い）２種の原子がある場合を考える。

2種の原子が交互にならんでおり、異なるばね定数k_1とk_2でつながっている(k_1>k_2とする)。単位胞は上図で示すように、２つの原子を含むようにとれる。周期をaとする。簡単のため、以下で２種の原子の質量が同じと仮定し、m_1=m_2=mとおく。

全ポテンシャルは、

とかけるので、

・ｎ番目のm_1の原子にはたらく力は

よって、運動方程式は、

・ｎ番目のm_2の原子にはたらく力は

よって、運動方程式は

運動方程式の解として、

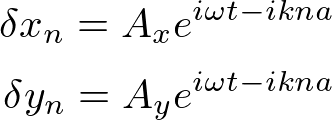
をそれぞれ代入すると、

A_x, A_yがゼロでない解をとるためには、行列式がゼロである必要がある（永年方程式）。ωについて解くと、分散関係

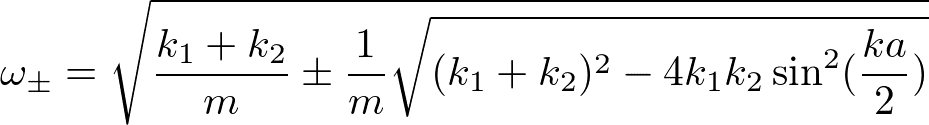
を得る。複雑な式だが、例えば

k=0で

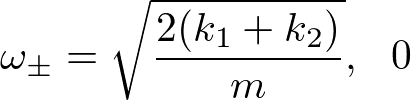
k=±(π/a)で

である。k - ω関係をプロットすると、

この場合も k → k+2π/a で周期的である。２原子の場合は２本の分散関係が得られる。それぞれ光学モード、音響モードと呼ばれる。光（photon)との相互作用は、photonとphononのエネルギーと運動量が一致する場合に起きる。（光速は音速より速いので）photonの分散関係 ω=ck >> vk より、光学モードとしか相互作用しない。

k→0のとき、運動方程式は、

となり、

・音響モードについて、ω=0を代入すると

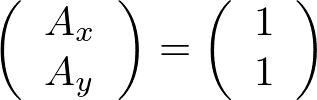
・光学モードについて、

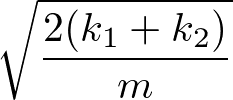
を代入すると、

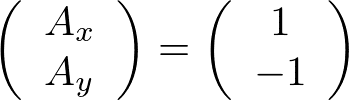
を得る。つまり、k=0付近で、音響モードは同じ方向に変位する（長い波長をもつ）が、光学モードは逆方向に変位する。２種の原子が＋とーの電荷をもっているとすると、光学モードでは電気双極子モーメントの波が誘起されることになる。

k_1 =k_2 のときは、前述した１種の原子の場合に帰着するはずである。これを分散関係で確認しよう。

k_1 =k_2 のときは、k=±(π/a)のギャップがなくなることに気づく。光学モードを外側に折り返す。

周期がaからa/2の半分になるのを考慮すると、第一ブリルアンゾーンは二倍になって、|k| ≦ 2π/a となる。

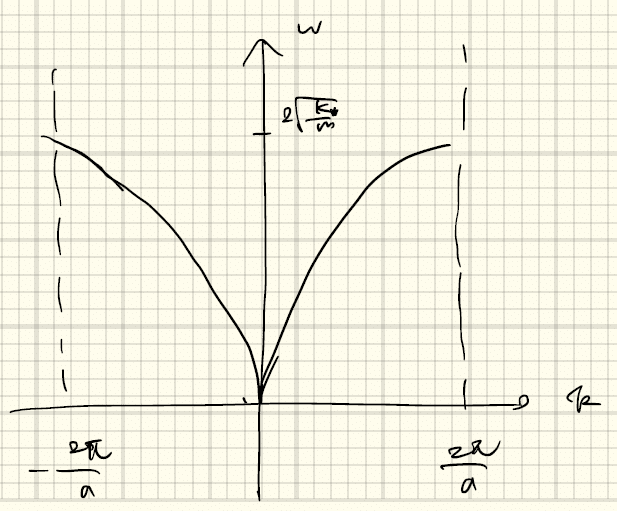
よって、１原子の場合に帰着される。

なお、一般にゾーン境界で群速度

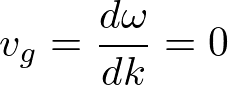
となっており、伝搬できない定常波の状態となっている。これは電子系のブリルアンゾーンの場合と同様にブラッグ条件を満たしている。

なお、３次元結晶の場合には、３次元自由度と対応して、１つの縦波と２つの横波がある。つまり、３個の音響ブランチが存在する。

（２）結晶の熱的性質

格子による比熱を考える。歴史的には、1819年にDulong-Petitの法則が見出された。それによると、比熱Cは１原子あたり

である。室温では結構成り立つことが知られている。しかしながら、明らかに温度変化しない式である。実際には、低温で、比熱は減少する。1896(1871?)年に、ボルツマンが、調和振動子のモデルを使って、Dulong-Petitの法則を説明した。

1907年に、アインシュタインが低温での比熱を説明するために、量子力学を使って調和振動子モデルを考えた。（つまり、低温での比熱のふるまいは量子力学を使って理解される。）

① Einsteinモデル

簡単のため一次元の調和振動子を考える。調和振動子のエネルギー固有値は

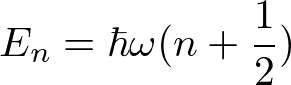
で与えられる。ここでは、ωは一定値

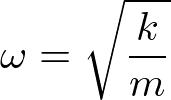
とおく。kはばね定数、ｍは原子の質量である。分配関数は、

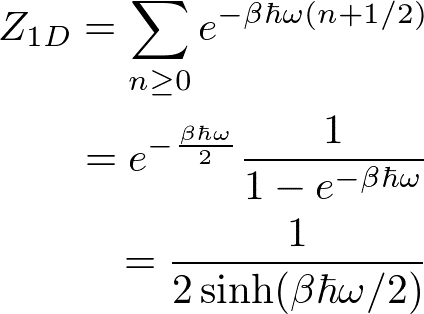
なので、エネルギーの期待値は

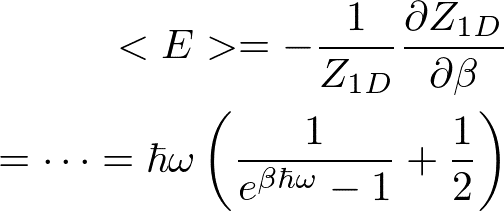
と求まる。最終式の第一項は、ボーズ分布関数である。波に平均何個のフォノンがいるかを表している。

比熱は、エネルギー期待値を温度で微分することで得られる。

高温で、β→0として、C→k_Bを得る。これは（１次元の場合の）Dulong-Petiの法則を再現する。これは高温では、エネルギー準位の間隔hωよりも熱エネルギーが十分大きくなるため古典的な場合に近づくと解釈できる。

３次元の場合には、

を使うと、エネルギー期待値は１次元の結果を使って

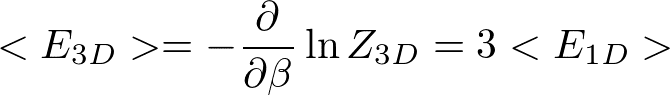
と書ける。よって比熱は、

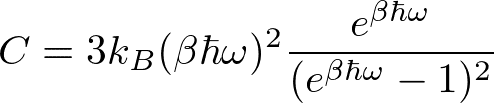
となる。高温で、3k_Bになり、Dulong-Petitの法則を再現する。また、低温では、β→∞として、指数関数的に０に向かうことがわかる。これはエネルギー準位の間隔より熱エネルギーが小さくなり、熱励起できなくなるからである。しかし実験的には、T^3に比例して減少することが知られており、実験と合わない。これは原子の振動が波として伝わる（格子振動）ことを無視しているためである。

②Debyeモデル

低温での格子比熱の振る舞いを正しく説明するのがDebyeモデルである（1912年 Peter Debye）。Einsteinモデルでは、ωは一定としたが、Debyeモデルでは、kに依存するとする。特に、原子の振動は音波なので、

の形をとるとする（光学モードは考えない）。３次元なので、縦波１つ＋横波２つの計３つの自由度がある。

Einsteinモデルでの１つの格子波がもつ平均エネルギー（３次元）は、群速度vを同じとして3倍すると

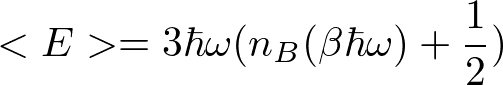
である(n_Bはボーズ分布関数）。全ての波について足し上げれば全エネルギーになり、ωがkに依存することを考慮すると、

ここで波の数を勘定している。ωはkベクトルの大きさ（kとおく）にしか依存しないので、極座標を使う。

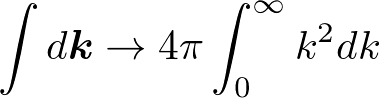
と、ω=vkの関係式を使ってkを消去すると、

ここで、

である。途中で、原子密度 n=N/Vという関係式を使った。ω_dはデバイ周波数

である。g(ω）の意味（⇒状態密度）については、後で考える。まずは、計算を継続し、比熱の式を出す。

より、比熱は、

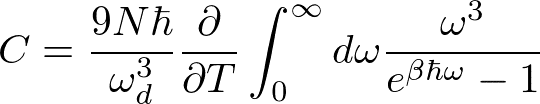
を計算すれば得られる。

とおいて積分を変形すると、

よって、比熱は温度Tの３乗に比例して増大する。以下で定義されるデバイ温度T_D

が用いられることがある。

これで低温比熱の温度依存性が説明されたわけで一件落着に見えるが、今度は、高温でのDulong-Petitの法則（C ～ 3k_B N (一定値））が成り立たない。実際、上式では、比熱は温度を上げると発散していく。

そこで、ωに上限を与えることを考える。自由度の数は、原子数×３であることを考慮して、

とし、∞までとっていた積分の上限をω_cutoffで制限する（g(ω)は状態密度）。つまり、修正したエネルギー期待値は、

である。上限が∞でないと、先ほどの比熱の計算における積分計算が実行できない（簡単にはならない）ように思える。しかし、低温においては、ωからｘへの変数変換

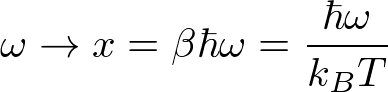
した際に、ｘの積分の上限が非常に大きくなるため、近似的に∞までの積分として扱える。よって、低温では先ほどの計算は近似的に正しい。

一方、高温においては、

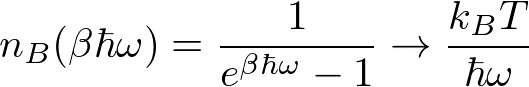
を使うと、

となり、Dulong-Petitの法則が成り立つ。

なお、

をg(ω)の定義を使って計算すると、

よって、カットオフ周波数は

となり、デバイ周波数に等しい。

このようにデバイモデルは、実験的に求められた低温と高温の格子比熱をよく説明する。低温でT^3則に従うことは、直感的には、熱エネルギー（k_B T）以下のエネルギー（振動数）をもつフォノンの数（「生きている」フォノンの数）がT^3に比例するためと理解できる。つまり、

より

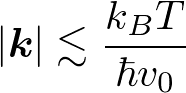
となる状態の数は

となり、T^3に比例することが示された。

しかし、一方で、デバイモデルには以下の欠点がある。

① cut offがad hoc（その場しのぎ）である

② ω=vk がｋが大きくても成立すると仮定している

③ 中間温度では実験と合わない

また、金属においては、電子比熱の寄与もあるため、実験と合わないことが知られている。③の中間温度での比熱の理論的取り扱いについては、この本に詳細な注意がある。

格子比熱については、歴史的な経緯もふくめて、『The Oxford Solid State Physics』に詳しい。

（３）結晶の力学的性質

 この節では、非調和効果を考える。非調和効果とは、調和振動子の近似では記述できない場合である。ひらたく言えば、調和振動子のポテンシャルは

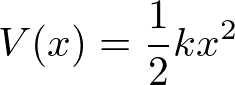
のように二乗の形で書けるが、ここにx^3とかx^4とか高次の項が入ってくる場合のことである。

非調和効果は、結晶の熱膨張や、弾性定数の温度・圧力依存性などを説明することが知られている。また、調和近似においては、２つの格子波は互いに作用しないので、フォノンは無限の寿命をもつ。よって熱伝導は無限大になってしまうが、非調和項があることにより有限の値に制限される。

熱膨張

熱膨張とは、温度が上昇すると体積・長さが増大する現象である。線膨張率

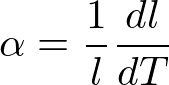
と、体積膨張率

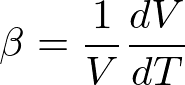
がある。αは通常、10^-5 [K^-1]くらいの大きさである。また、等方的なときはα=β/3である。

簡単なモデルで熱膨張を考える。原子間隔をｘとおいて、ポテンシャル

を考える。第二項が非調和項に相当する。非調和項は調和項に比べると小さいと仮定する。

原子間隔の平均値<x>は、温度とともに変化する。<x>は、

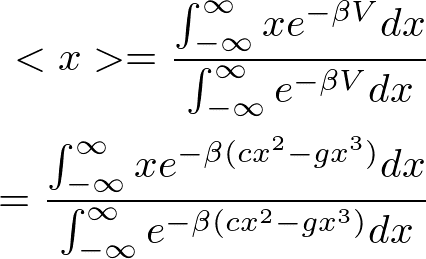
 と表せる。分母は、

となる。ここで、非調和項が十分小さいと仮定して変形した。また、最後の式を求めるところでは、奇関数の積分がゼロになることを使った。また、分子は、

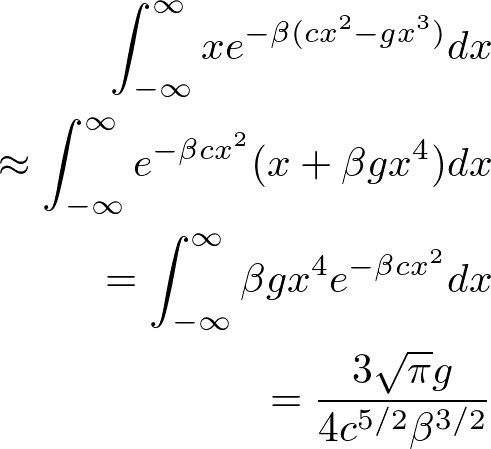
以上より、

よって温度に比例して<x>は大きくなる。調和項しかない（g=0）場合は、熱膨張はゼロになることがわかる。また、４次の項fx^4があっても、奇関数の積分はゼロなので、効かない。ｘに対して非対称なポテンシャル(~x^3）によって、振動の中心がずれていくことにより、<x>はゼロでない値をとると考えることができる。

非調和効果は、『物性物理学』（永田一清）に簡潔にまとめられている。