力学§７：剛体

§７．１　剛体の運動

剛体とは、大きさはあるが変形しない物体である。これまでの質点系の運動に関する知識をベースに剛体の運動を解析する。

剛体の内部のそれぞれの位置は、位置ベクトルrで指定できる。すなわち、大雑把には、剛体は多質点系 r_A, r_B, r_C, ...の集まり（ただし微小体積分の広がりをもつ）と思うことができる。このことを基礎とし、多質点系での議論における全質点の和Σを積分∫に置き換えることで剛体の運動の記述を行う。

まず、結論から述べると、剛体の運動は、

　　　　①重心の並進運動＋②重心周りの回転運動

で記述できる。①の並進運動については、剛体は大きさがあるが、重心という質点の運動に帰着できることになる。②の回転運動は、大きさがあることがきいてくるために現れる。つまり、大きさがあると、力のつり合いだけでは不十分である（質点は回転しないが剛体は回転しうる）。②は回転運動の記述であるので角運動量を使って考えることになる。

①と②のそれぞれの運動について、剛体の基礎となる多質点系で考察する。

①重心の運動方程式：　内力（相互作用）は、全部の質点での和を考えると打ち消しあう。従って、外力だけ残る。つまり、

左辺について、重心の定義により

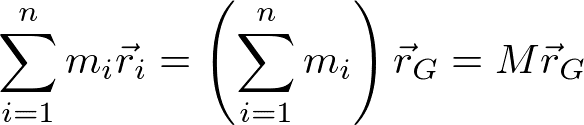
であるので（M：全質量）、重心の運動方程式は、

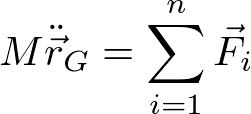
と書き直せる。すなわち、重心の並進運動は、外力の和に対する質点（質量M）の運動と見なせる。

②重心周りの回転運動：　回転運動の記述のために、全角運動量を考える。角運動量の定義を思い出すと、ｎ質点系の全角運動量は

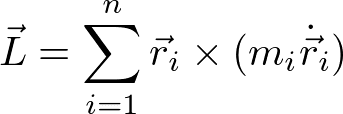
である。重心周りの回転運動を考えるために、以下のように位置ベクトルを分解する。

第二項が重心からの相対位置ベクトルを表す。全角運動の式に代入して整理すると、

最後の式で第二項と第三項はゼロになる（理由は後述）。従って、

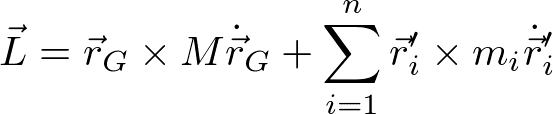
が得られる。第一項が（原点周りの）重心の角運動量、第二項は重心の周りの角運動量である。それぞれを、自転と公転と呼ぶ人もいる[4]。なお、上記の式を得るために、

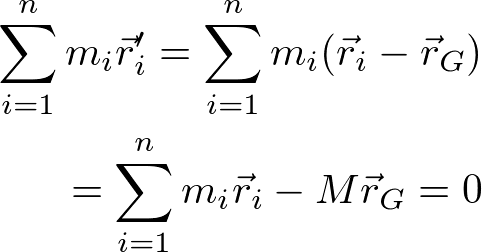
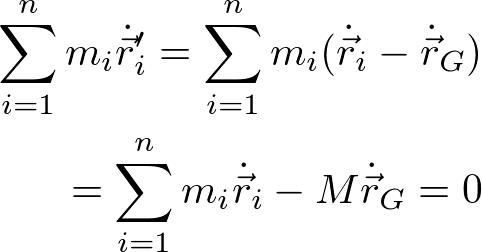
を利用した。

次に、回転運動を考えるために、全角運動量の時間微分を考える。

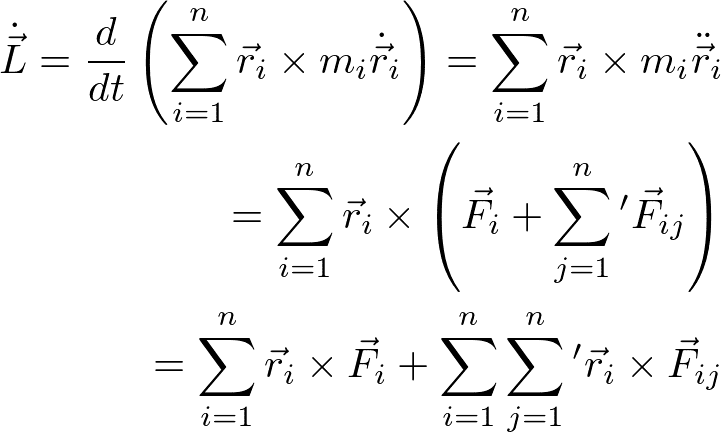
ここで、Σ'はj=iを除く和を表す。最後の式の第二項はゼロになる。なぜならば、

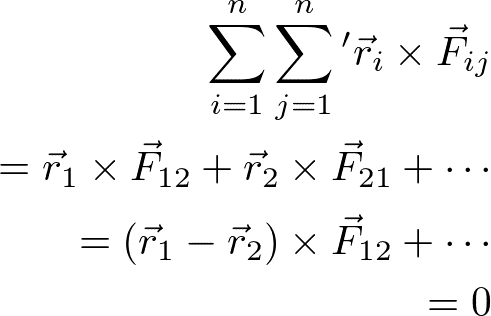
ここで、F_12 という1-2間にはたらく内力は、r_1 - r_2 というベクトルに平行である（つまり外積はゼロ）ことを利用した。以上により、

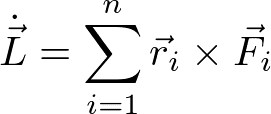
と簡単な式が得られる。右辺は力のモーメントの和であるので、原点周りの角運動量の変化は外力のモーメントの和に等しいことがわかる。これが（原点周りの）回転運動を表す式である。

しかしながら、「②重心周りの回転運動」と最初に書いたように、原点周りの回転運動の式ではなく、重心周りの回転運動の式の方がよく使われる。この場合は、原点周りの重心の回転運動を無視して、

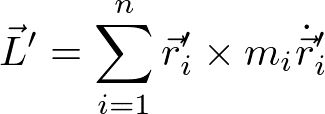
の時間変化を考える。重心の回転運動を考えなくてよい理由は、①で得られた重心の並進運動の方程式より、

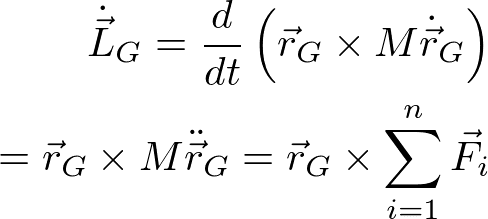
となり、これは①の重心の並進運動の方程式に左からr_Gの外積をとっただけで、新しい式ではないからである。さて、重心周りの回転運動に話を戻すと、L'の時間微分は、

ここで、さっきも出てきた関係式である

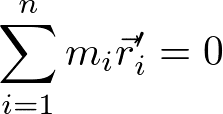
を使った。さらに式を変形して、

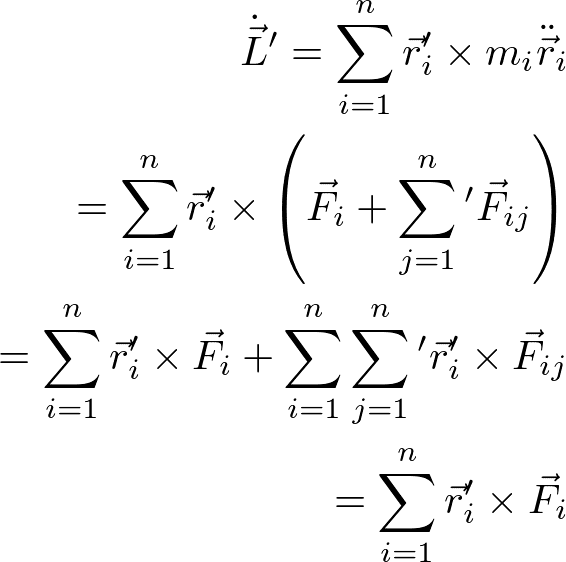
を得る。ここで、

を使った。 r_1' - r_2' と F_12 は平行であるため、外積はゼロになる。以上により、

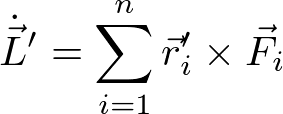
を得る。右辺は重心周りの外力のモーメントである。原点周りの回転運動の式と似た式であるが、（重心の回転運動は考えずに）重心を原点として回転運動を考えればよいということになる。

以上の多粒子系の議論をまとめて、剛体の運動を理解した気になると、最初に述べたとおり、

　剛体の運動：①重心の並進運動＋②重心周りの回転運動

となる。繰り返しだが、②は原点周りの回転運動を考えてもよい（重心の回転が情報として重複するだけ）。式でもう一度書けば、①は

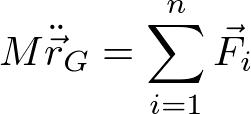
で、②は

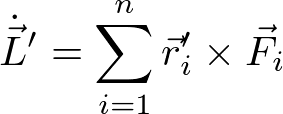
である。また、式として６個の方程式が出てくるが、これは独立な座標変数が６個であることと対応している。

このように剛体の運動の解析は、重心という特別な点があることによって随分と簡単になっている。今までの式変形を見直すと、第三法則があることにより内力の項が消えること、運動方程式が位置座標に線形であることが重要であった。

§７．２　剛体のつり合い

質点は回転しないが、剛体は回転することができる。従って動かないことと回転しないことがつり合いの条件となる。前節より、動かないことは外力の総和がゼロ、回転しないことは力のモーメントの和がゼロという条件で書かれる。

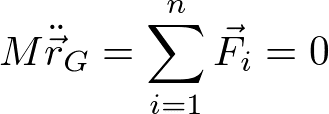
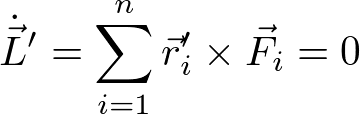
有名な例は、てこ（の原理）である。以下の図のように、左端に質量mの重りがあり、右端を力Fで支える。

力の総和がゼロより、

力のモーメントがゼロより、

よって、力Fは、 

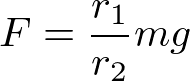
である。

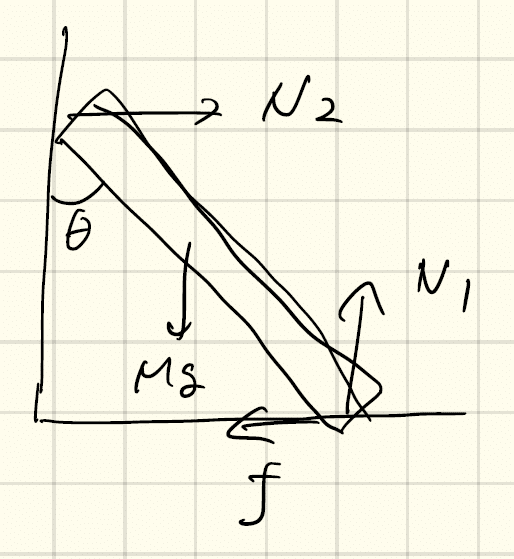
問７．１　下図のように、摩擦のない壁に棒を立てかける。重力Mgに加えて、床と壁から垂直抗力N_1とN_2がはたらく。力fにより、棒はつり合っている。棒の長さをLとする。このとき、力fを求めよ。また、力のモーメントを計算するとき、棒の中心（重心）を原点としても、壁の角（壁と床の交点）を原点としても同じ結果が得られることを確認せよ。

§７．３　固定軸をもつ剛体の運動

固定軸をもつ剛体の運動は、コマの回転をイメージしてよい。（ただし、コマのようなきれいな円形の形をしている必要はない。）固定軸があるため、剛体は並進運動はできない。そのため、この節では回転だけを考えることになる。

回転軸をｚ軸のとり、ｚ軸まわりの回転運動を考える。回転運動の方程式に立ち戻ると、ｚ軸回りの角運動量を考え、

が考えるべき運動方程式となる。(L_xとL_yは考えなくてよい）

L_zを計算するにあたり、§７．１では多質点系の計算でごまかしたが、以下のように粗視化を行うことで積分を用いた計算を行う。粗視化においては、剛体内の位置ベクトルrにおける微小体積ΔV（質量ΔM）において、質量密度が

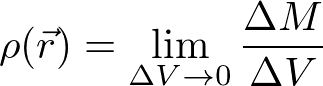
であると仮定する。質量密度を用いて、Σによる和を以下の通りに積分∫に書き換える。

円筒座標

を用いると、

なので

を得る。ここで、回転速度は剛体内で一定であることを使って積分の外に出した（各部分が異なる角速度をもてない）。I_zを慣性モーメントと呼ぶ。慣性モーメント

は時間によらず、剛体の質量密度と形が分かれば計算可能である。

問７．２　慣性モーメントの次元は？

慣性モーメントを用いると、回転の運動方程式は

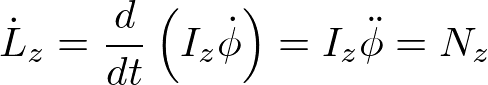
となる。ニュートンの運動方程式と似た形をしている。式の形は似ているが、ニュートンの運動方程式を解くときと異なり、運動方程式を解く前にまず「質量」に相当する「慣性モーメント」を計算する必要がある。

問７．３　下図のような円筒（外半径a、内半径b、高さl）の慣性モーメントI_zを求めよ。

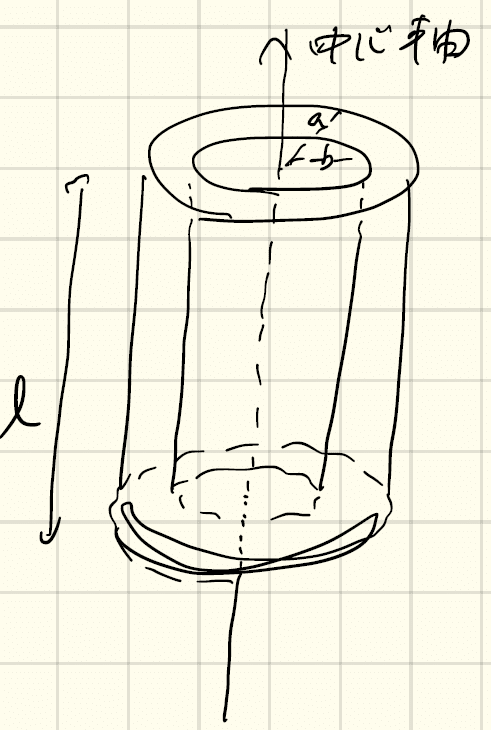
問７．４　下図のような、３辺がa, b, cの質量Mの直方体の慣性モーメントI_zを、直方体の中心を通る軸の周りで計算せよ。

慣性モーメントに関して、以下の定理が成り立つ。

質量Mの剛体の任意の軸の周りの慣性モーメントIは、その軸と重心との距離をhとすると、

で与えられる。ここで、I_Gは重心周りの慣性モーメントである。

なぜならば、軸周りの慣性モーメントIは、軸を原点とした剛体内の位置ベクトルrを重心位置r_Gからの相対位置r'を用いて書き直すと、

ここで、

（ｙ成分も同様）を用いた。

上記の定理は、重心からずれた軸（つまり中心からずれていて計算が面倒になりそうな軸）周りでの慣性モーメントを計算するのに役に立つ。

回転運動の運動エネルギーも、慣性モーメントを用いて書き直すことができる。

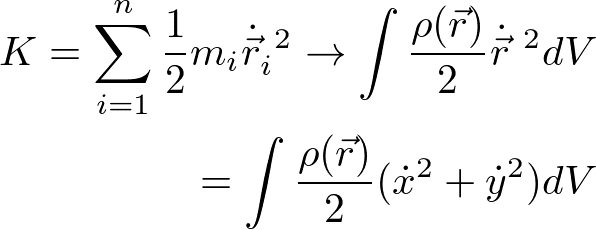
ここで円筒座標を用いると、

となるので（固定軸なので、動径方向の時間微分はゼロ）、

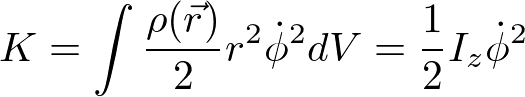
以上より、質点の一次元運動と剛体の回転には、以下のような類似関係がある。

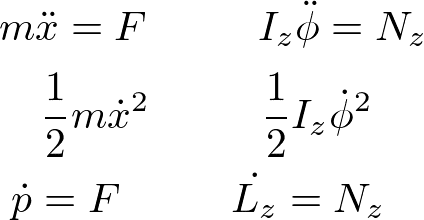
より、

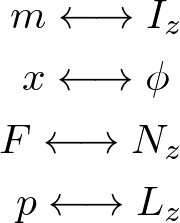
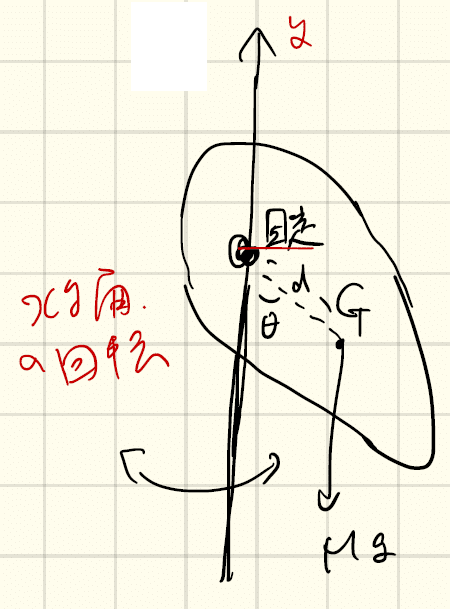
問７．５　以下の図のような実体振り子の運動を考える。xy面内で、重心Gからdだけ離れた固定軸の回りで、剛体が振り子運動をする。鉛直方向をy方向にとっている。剛体の慣性モーメントをIとおく。実体振り子の運動の周期Tを求めよ。また。ｄを変化させるとき、周期が極小となる条件を求めよ。

§７．４　剛体の平面運動

以下の図のように、回転しながら（丸い）剛体が落ちることを考える。摩擦Fがないときは滑り落ち、摩擦があると回転しながら落ちる。

ｘ軸を坂道方向にとる。はたらく力は、重力Mg、垂直抗力N、摩擦力Fである。これまで学んだことから、重心の並進運動と重心周りの回転運動に分けて式を立てる。まず、重心の並進運動は、

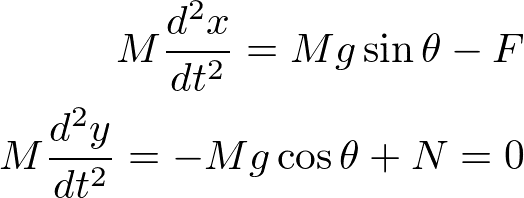
である。ここで、ｙ方向には運動しないことを考慮した（ｘ方向だけ考えればよい）。重心（円の中心）周りの回転運動は、慣性モーメントIを使って

と書ける。また、

が成り立つ。以上より、Fを消去することで、

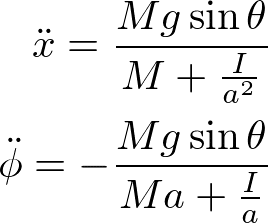
を得る。並進運動の加速度は、ずり落ちる場合（F=0の場合）に比べて、

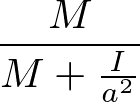
倍になっている（遅くなっている）。これは回転にエネルギーをとられているからという見方ができる。また、慣性モーメントが大きい方が落ちる速度は遅い。問７．３より、一様に詰まった円柱よりも中空の円筒の方が（両者の質量Mが一定の場合には）慣性モーメントは大きいので、中空の方が遅く落ちることになる。

エネルギー保存則が成り立つことを確認しよう。

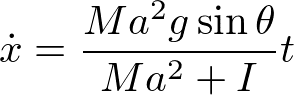
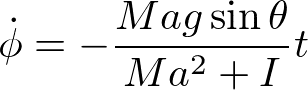
より、並進運動と回転運動の運動エネルギーは

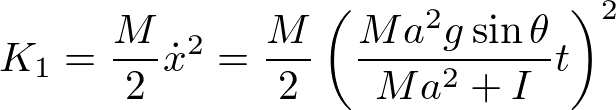
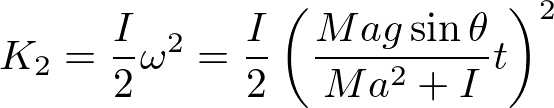
となる。足すと、

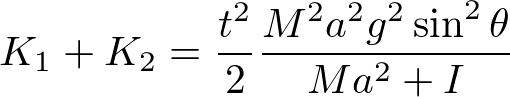
となる。一方、位置エネルギーの変化ΔUは

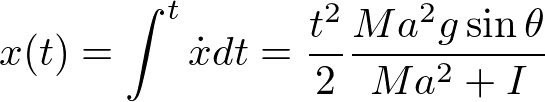
を使うと、

を得る。よって位置エネルギーの変化は運動エネルギーの変化に等しい。