力学§5:運動する座標系
前節までは原点を固定し、座標系が時間変化しない場合を考えた。この節では座標系が固定されない場合の取り扱いを考える。
§5.1 ガリレイ変換
座標系が等速直線運動する場合をガリレイ変換と呼ぶ。

上の図のように、点Pの位置を2つの座標系で表すと、

となる。ここで、変換後の座標系の原点O'は、一定速度Vで元の座標系から見て運動することを使って式変形した。加速度は、時間に対して二階微分をとるので、定数項および速度に比例する項は消えて、どちらの座標系でも同じになる。つまり、運動方程式が同じになる(慣性系)。
一方、新しい座標系が加速度をもつ場合、つまり上の式で
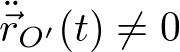
の場合には、
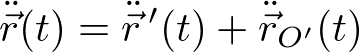
なので、もともとの運動方程式
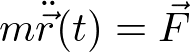
は、座標系の変換後に
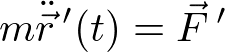
![]()
へと変わる。非慣性系においては、力に見かけの力である慣性力が加わる。非慣性系の有名な例としては、エレベータの中がある。
問5.1 下図のように、物体が坂道を滑り落ちる場合を考える。

観測する人間が止まっている場合は、エネルギー保存則は
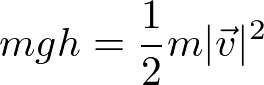
であるが、右に-Vの速度で動いている人から見ると、
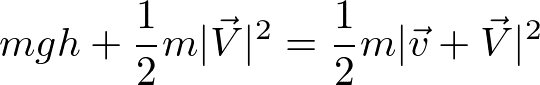
になる気がするが、左辺と右辺は一致しない。(右辺にmv・Vというお釣りの項が出てくる。)一致しない理由は何か?[3]
§5.2 回転する座標系
今度は、z軸のまわりに回転する座標系を考える。このとき慣性力が生じることを示す。
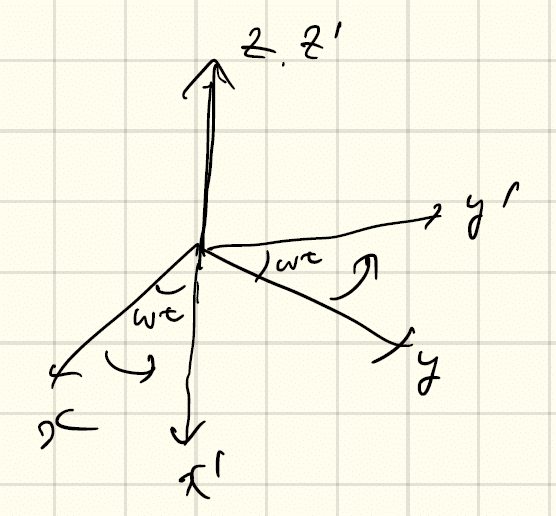
まず、ある位置ベクトルrを元の座標系('なし)と回転する座標系('あり)の2つの座標系で表現する。
![]()
今、z軸の回りに回転するので、単位ベクトルの間の関係は
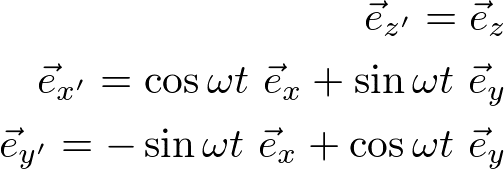
である。ここで、e_x'とe_y'の方は回転しているので時間変化するが、e_xとe_yの方は固定されているので時間依存しないことに注意する。
我々の目標は、上述の位置ベクトルを時間微分して加速度を求める(そして運動方程式を書き下す)ことである。その準備として単位ベクトルの時間微分を求める。実際に計算すると、

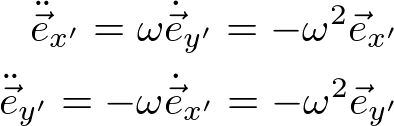
と求まるので、速度ベクトルは、

ここで、角速度ベクトルω=(0,0,ω)を定義した。同様に、加速度ベクトルは、
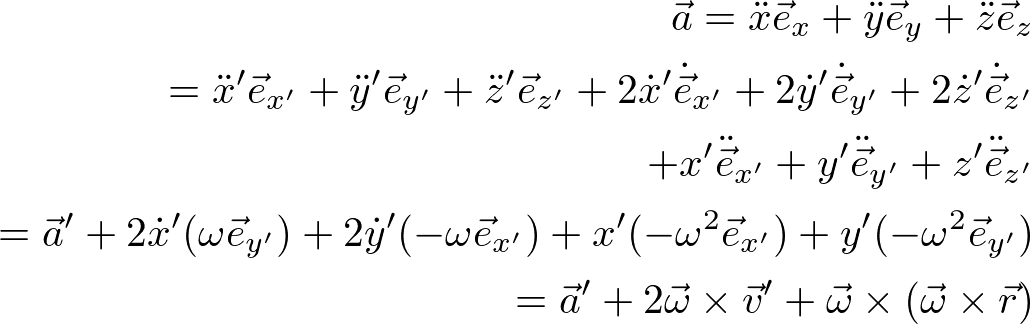
よって、運動方程式
![]()
は、

へと変換される。力に慣性力が2つ加わり、第二項はコリオリ力、第三項は遠心力と呼ばれる。遠心力は、距離に比例して大きくなる力である。
コリオリ力は、ω>0のときは進行方向に対して右向き、ω<0のときは進行方向に対して左の力となる。コリオリ力のイメージとして、回転する円盤状の台の上に立ち前方にボールを投げることを考える。乗っている円盤台が左回りに回るとき、ボールは投げた人から見て、右に曲がっているように見える。(静止している人から見るとまっすぐ飛ぶ。)一方、円盤が逆に右回りに回ると、ボールは左に曲がるように見える。
問5.2 遠心力はどちら向きのベクトルか。
