
memo3
線形システムの安定性は極によって決まる。システムの安定性をエネルギーに関連つけることで非線形性においても安定性を考えることができる。
このことを拡張したものがリアプノフの安定定理
平衡点がリアプノフの意味での安定とは
任意に与えられたε>0に対しδ(ε)>0が存在し $${||x_0||<δ(ε)}$$の時、任意の時刻tで||x(t)||<εであれば、平衡点$${x_e=0}$$は安定
任意のε>0に対しδ(ε)>0が存在するということはε>x>0のどのxに対しても特定のδ(ε)>δ(x)>0が存在するということ。つまりε>xであればxはδ(ε)を上限とする有界であるということ。そして||x0||<δ(ε)の時というのは初期値がδ(ε)を上限として有界であるということ。
||x0||<δ(ε)の時というのは初期値がδ(ε)を上限として有界であるという時にどの時間のxもε>xであればε>x>0のどのxに対しても特定のδ(ε)>δ(x)>0が存在するということなのでxはδ(ε)を上限とする有界であるということになる。つまり発散しないということになる。
この時を平衡点は安定という。
この条件を満たす時に$${\lim_{{t \to \infty}} ||x(t)|| = 0}$$
である時に平衡点は漸近安定であるという。
また任意の初期値$${x_0}$$に対して$${\lim_{{t \to \infty}} ||x(t)|| = 0}$$となるならばシステムは大域的漸近安定であるという。
リアプノフの安定定理において
正定関数の微分が半負定関数ならば平衡点は安定である。
また$${\dot{\phi}(x(t))}$$が負定関数ならば平衡点は漸近安定である。
これらを満足するスカラー関数をリアプノフ関数という。
線形な零入力システムに対し任意の与えられた$${\bf{Q=Q^{T}>0}}$$に対して$${\bf{PA+A^{T}P=-Q}}$$を満足する解$${\bf{P=P^{T}>0}}$$が唯一存在することと漸近安定であることは等価である。
これは定めたQに対して$${\bf{P=P^{T}}}$$が正定であるかにより判別することができる。またこの時定めたQは正定である必要がある。
任意の列ベクトルに対する二次形式が正となる行列を正定行列という。この判別は固有値による判別、もしくはシルベスターの判別条件により行うことができる。
固有値による方法
固有値が実数であり、かつ全て正であればそのときに正定行列である。
例えばこのように計算する。
P = [4 1
1 3];
eig(P)どちらも実数かつ正なので正定である。
ans =
2.3820
4.6180Qが半正定でも安定性を判別できる場合について。
Qが可観測であるとすると$${\bf{PA+A^{T}P=-Q_o^{T}Q_o}}$$
を満足するPが唯一存在することと漸近安定であることは等価である。
lyapを用いてPを求めることができる。
clear
A = [0 -5
1 -2];
eig(A)
Q = eye(2);
P = lyap(A',Q);
eig(P)Aの固有値の実部が負で安定、Pの固有値は実数かつ正で安定
ans =
-1.0000 + 2.0000i
-1.0000 - 2.0000i
ans =
0.2929
1.7071もう一つの場合
clear
A = [0 -5
1 -2];
eig(A)
Qo = [0 1];
Vo = obsv(A,Qo)
rank(Vo)
Q = Qo'*Qo
P=lyap(A',Q)
eig(P)rank=2より可観測 Pの固有値は実数かつ正である
ans =
-1.0000 + 2.0000i
-1.0000 - 2.0000i
Vo =
0 1
1 -2
ans =
2
Q =
0 0
0 1
P =
0.0500 0.0000
0.0000 0.2500
ans =
0.0500
0.2500リアプノフ関数の挙動
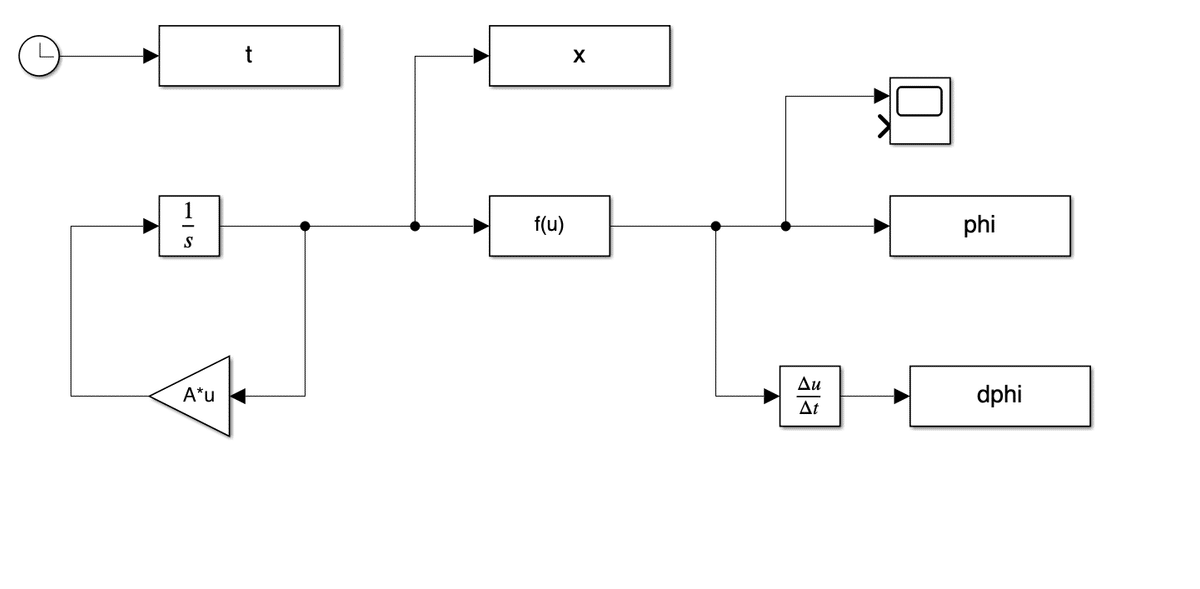
clear
A = [0 -5
1 -2];
eig(A)
Q = eye(2);
P = lyap(A',Q);
eig(P)
x0=[1 0]';
sim('lyapnov.slx');最適レギュレータ
定量的に表した評価関数を最小化するようにコントローラを設計する。
$$
J = \sum_{i=1}^{n} q_i J_{x_i} + \sum_{j=1}^{p} r_j J_{u_j} = \int_{0}^{\infty} \left( \sum_{i=1}^{n} q_i x_i(t)^2 + \sum_{j=1}^{p} r_j u_j(t)^2 \right) dt
$$
の評価関数に関して重みqi やrjを調整することで応答を調整できる。
最適レギュレータ問題
$${\bf{Q=Q^T>0}}$$
$${\bf{(Q_o,A)}}$$が可観測かつ$${\bf{Q=Q^T=Q_o^TQ_o\ge0}}$$のいずれかを満足する重み行列Q Rに対して
$$
J = \int_{0}^{\infty} \left( x(t)^T Q x(t) + u(t)^T R u(t) \right) dt
$$
を最小化するコントローラを求める問題を最適レギュレータ問題という。
最適レギュレータ問題の解ゲインKは
$${\bf{K_{opt}:=-R^{-1}B^TP_{opt}}}$$
によって得られる。
Pはリカッチ方程式を満足する実数の正定対象解であり唯一に定まる。
リッカチ方程式の数値解法として有本ポッター法がある。
最適レギュレータにより設計されるサーボシステムを、最適サーボシステムと呼ぶ。
制御対象
$$
\begin{cases} \dot{x}(t) = A x(t) + B u(t), \quad x(0) = x_0 \\ y(t) = C x(t) \\ \eta(t) = x(t) \end{cases}
$$
定常値について
$$
\begin{cases} 0 = A x_\infty + B u_\infty \\ y_c^{\text{ref}} = C x_\infty \end{cases} \Rightarrow \begin{bmatrix} x_\infty \\ u_\infty \end{bmatrix} = \begin{bmatrix} A & B \\ C & 0 \end{bmatrix}^{-1} \begin{bmatrix} 0 \\ y_c^{\text{ref}} \end{bmatrix}
$$
$${\dot{w}=e:=y^{ref}-y}$$の両辺の時間積分
$$
\int_{0}^{t} \dot{w}(t) dt = \int_{0}^{t} ( \dot{w}(t) - \dot{w}_0 ) dt = \int_{0}^{t} e(t) dt \Rightarrow w(t) = w_0 + \int_{0}^{t} e(t) dt
$$
最適サーボシステムを構成する積分型コントローラ
$$
u(t) = Kx(t) + G \int_{0}^{t} e(t) dt + F_a y^{\text{ref}}(t) + F_b x_0
$$
ここで
$$
y^{\text{ref}}(t) = y_c^{\text{ref}}, \quad e(t) = y^{\text{ref}}(t) - y(t)
$$
$$
K = -R_e^{-1} B^T P_{12}, \quad G = -R_e^{-1} B^T P_{12}
$$
$$
F_a = \left[ -K + 2 G P_{22}^{-1} P_{12}^T \right] \begin{bmatrix} A & B \\ C & 0 \end{bmatrix}^{-1} \begin{bmatrix} 0 \\ I \end{bmatrix}, \quad F_b = -2 G P_{22}^{-1} P_{12}^T
$$
となる。Fa Fbは積分コントローラを構成するゲイン行列。Fa は目標値 𝑦ref(𝑡)yref(t) に基づく制御信号のゲイン行列。目標値が一定の場合、この行列はシステムが目標値に正確に追従するように制御信号を調整する。
Fb は、初期状態 𝑥0x0 に基づく制御信号のゲイン行列。この行列は、システムの初期状態に応じて適切な制御信号を生成するために使用される。
最適レギュレータではKのみ。
積分型コントローラの最適サーボシステムではK G Fa Fbの四つのゲインを求めてコントローラを作成する。
積分型コントローラの最適サーボ
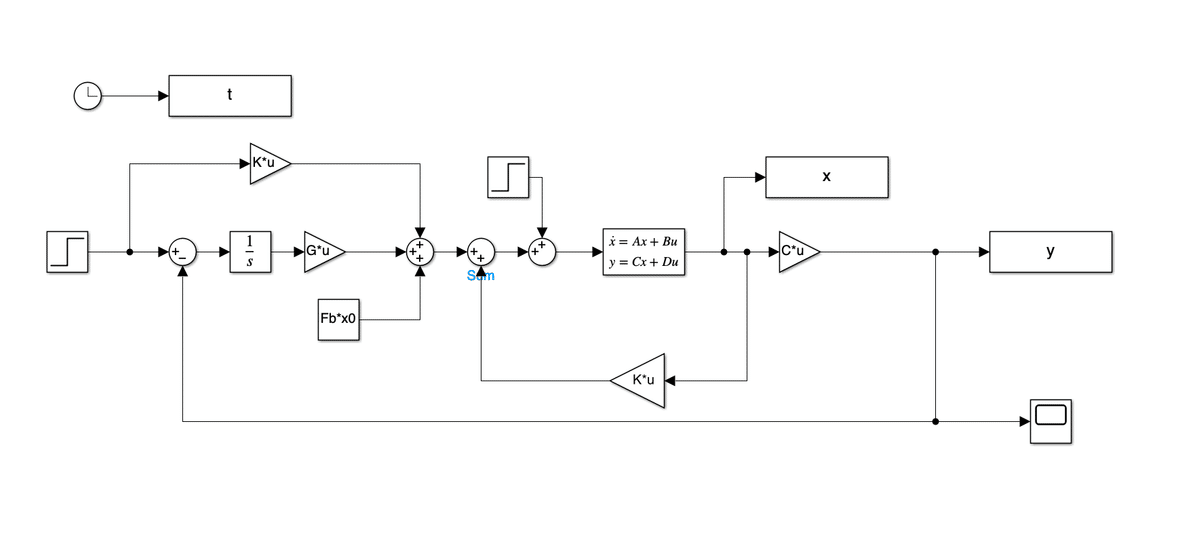
clear
A = [0 1 0 0
-4 -2 4 2
0 0 0 1
2 1 -2 -1];
B = [0;2;0;0];
C = [0 0 1 0];
Ae = [A zeros(4,1)
-C zeros(1,1)];
Be = [B
zeros(1,1)];
Q11 = 100; Q22 = 600;
Qe = [ C'*Q11*C zeros(4,1)
zeros(1,4) Q22];
Re = 1;
Pe = care(Ae,Be,Qe,Re);
P11 = Pe(1:4,1:4)
P12 = Pe(1:4,5)
P22 = Pe(5,5)
K = -inv(Re)*B'*P11
G = -inv(Re)*B'*P12
MO = [A B
C 0];
Fa = [-K+2*G*inv(P22)*P12' 1]*inv(MO)*[zeros(4,1);1]
Fb = -2*G*inv(P22)*P12'
%Fa =0;
%Fb=zeros(1,4);
x0 = [0 0 0.25 0]';
sim('simulink_optimal_servo.slx');いいなと思ったら応援しよう!

