
[階層ベイズ] ベータ分布のパラメータの超事前分布
階層ベイズモデルにおいて、尤度を二項分布、事前分布をベータ分布とした場合の、ベータ分布のパラメータ$${a, b}$$の超事前分布の選択方法について調べたことのメモ。
結論
別にどれでもいい。
よほど変な分布選ばない限り実用的には大きな問題にはならなさそう。多分。
共通の分布でa, bを直接モデル化する
まず、a, bの両方を直接モデル化している例から。
1. ガンマ分布
特に理由無く恣意的にガンマ分布を使っている例。
$$
Y_i ∼ Binomial(n_i, p_i)\\
p_i ∼ Beta(a, b)\\
a ∼ Gamma(4, 0.5)\\
b ∼ Gamma(4, 0.5)
$$
2. ハーフコーシー分布
ハーフコーシー分布を使う例。リファレンスは載せられませんが、この流儀を見たことがあるので。ハーフコーシー分布のハイパーパラメータの決め方も弱情報になるように適当に考慮するような話もあった気がする。
$$
Y_i ∼ Binomial(n_i, p_i)\\
p_i ∼ Beta(a, b)\\
a ∼ HalfCauchy(\cdot)\\
b ∼ HalfCauchy(\cdot)
$$
ちなみに、分散の超事前分布には、(分散が未知の正規分布の共役事前分布である)逆ガンマ分布が伝統的に使われていたが、ハーフコーシー分布、あるいはハーフt分布が適切という説があるようです。
平均と集中度を別々にモデル化する
次に、平均$${\mu = \frac{a}{a+b}}$$、集中度$${\eta = a + b}$$に対してそれぞれ別の分布を仮定する方向性。
3. 平均:ベータ分布/集中度:ロジスティック分布の指数
平均にベータ分布、集中度(サンプルサイズ)にロジスティック分布の指数を用いる例。平均に対して事前知識が無い場合は、ほぼ無情報となる$${Beta(1, 1)}$$を選択する。集中度のパラメータ$${n^*}$$は代表的な試行回数。
$$
Y_i ∼ Binomial(n_i, p_i)\\
p_i ∼ Beta(a, b)\\
a = \mu\eta\\
b = (1 − \mu)\eta\\
\mu ∼ Beta(1, 1)\\
\log\eta ∼ Logistic(\log n^∗, 1)
$$
4. 平均:ベータ分布/集中度:ハーフコーシー分布 or 無情報分布
平均にベータ分布、集中度にハーフコーシー分布または無情報分布を用いる例。平均のパラメータはデータから試行錯誤して決定するようだ。
$$
Y_i ∼ Binomial(n_i, p_i)\\
p_i ∼ Beta(a, b)\\
a = \mu\eta\\
b = (1 − \mu)\eta\\
\mu ∼ Beta(\cdot)\\
\log\eta ∼ HalfCauchy(\cdot)
$$
もともとは以下の書籍から来ているようだ。この本はなかなか手に入れられていない。今度確認する。
実験
私はただのユーザなので、上の四つが実際的に違いが生まれるのかを簡単に調べました。
ベルヌーイ過程をとる10個の系列の観測データを適当に作ります。真の$${p_i}$$は適当なベータ分布から生成します。階層モデルなので$${n}$$はバラバラでも大丈夫です。
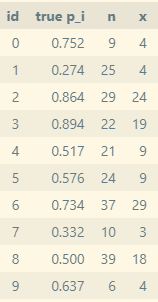
PyMCでモデルをつくってMCMCで事後分布をサンプリングします。
def model_3(n_data, x_data, n_groups, mu_alpha=1, mu_beta=1, n_star=100, s_logeta=1):
# https://bayesball.github.io/BOOK/bayesian-hierarchical-modeling.html#example-deaths-after-heart-attack
with pm.Model() as model:
# hyper-prior
mu_logeta = np.log(n_star)
mu = pm.Beta('mu', alpha=mu_alpha, beta=mu_beta)
eta = np.exp(pm.Logistic('log_eta', mu=mu_logeta, s=s_logeta))
# prior
p = pm.Beta('p', alpha=mu * eta, beta=(1 - mu) * eta, shape=n_groups)
# likelihood
x = pm.Binomial('x', n=n_data, p=p, observed=x_data)
return model
def inference(n_data, x_data, model_func, **kwargs):
n_groups = len(n_data)
model = model_func(n_data, x_data, n_groups, **kwargs)
print(model.basic_RVs)
with model:
trace = pm.sample(
draws=1000,
tune=500,
chains=3,
random_seed=1,
return_inferencedata=True
)
return trace以下、結果です。
青の実線が階層モデルで推論された事後分布で、橙の破線は(ほぼ)無情報のベータ分布を事前分布として単にデータにしたがって更新した場合の事後分布です。
同じようなグラフが並んでいるだけなので特に見る必要はないです。
1. ガンマ分布
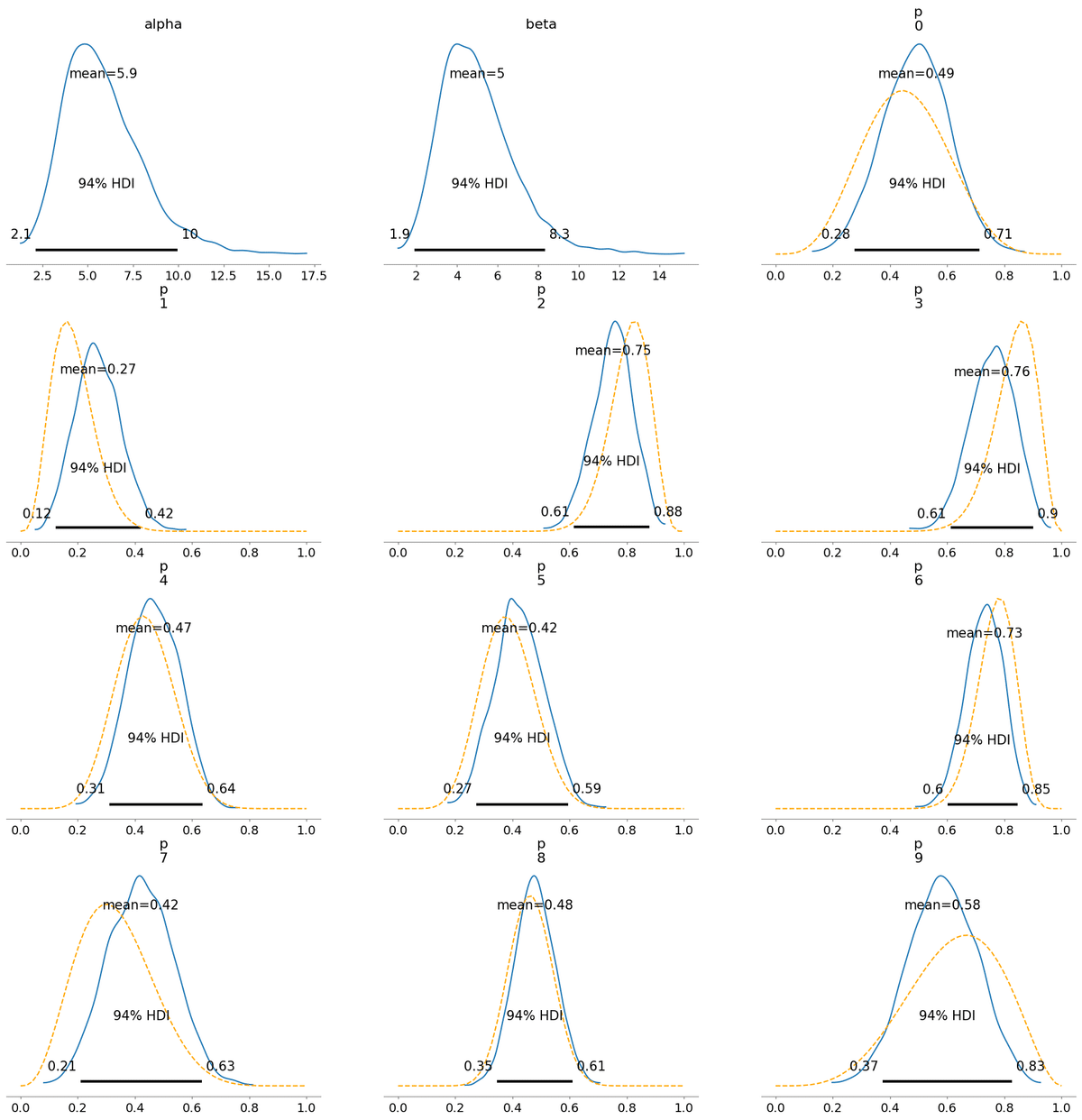
2. ハーフコーシー分布
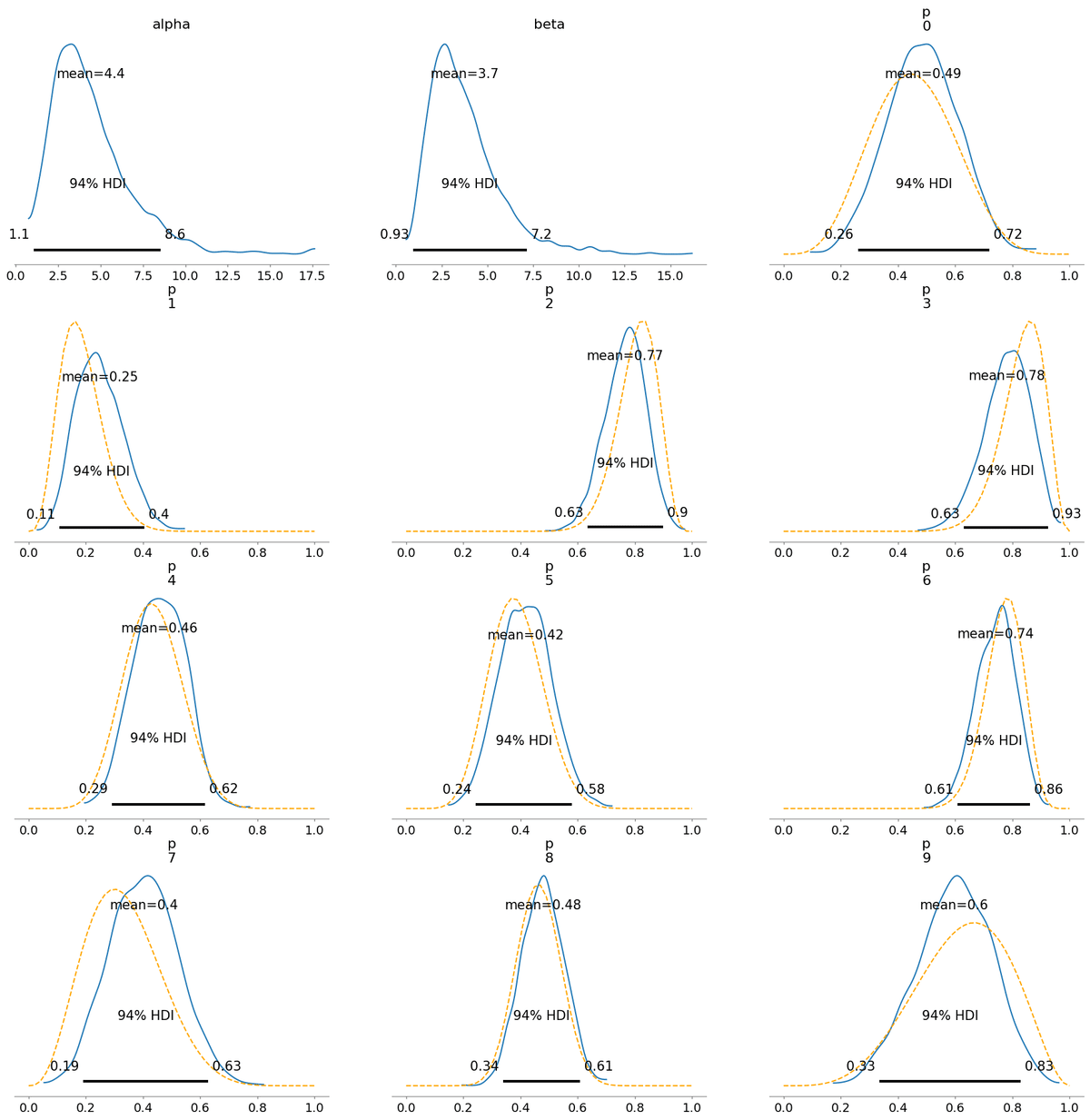
3. 平均:ベータ分布/集中度:ロジスティック分布の指数

4. 平均:ベータ分布/集中度:ハーフコーシー分布

どの方式でも大差ありませんでした。結局MCMCするならよほど筋の悪い分布にしない限りあまり深く考えなくていいのかも。
この記事が気に入ったらサポートをしてみませんか?
