駿台中学生テストの確実圏偏差値60の高校は、倍率3倍であれば、最下位合格ラインは偏差値53
これまでの記事で、駿台中学生テストの偏差値を、高校を比較する指標として扱ってきました。その際には、合格者平均偏差値は確実圏偏差値ー6、可能圏偏差値ー2という計算をしてきています。これはネットに一時期掲載されていた合否追跡データのグラフから概算で出した数字です(今でも転載したブログが残っているようです)。
今回はこのような分布になるモデルを検討し、そこから最下位合格ラインの偏差値を推定してみます。まずは分析のためのデータ準備を行います。
1. 駿台中学生テストの判定偏差値の分析
少し古いですが、2022年第5回の駿台中学生テスト(高3年対象)の合格判定ラインの偏差値を調べたことがあります。対象は全国の1,126校です。男女別に設定されている場合は、単純平均値を採用します。
調べてみると、確実圏偏差値(合格可能性80%)と可能圏偏差値(合格可能性60%)の差(20%幅)は平均で6.1でした。また、確実圏偏差値に対する20%幅の分布を取るとこのグラフのようになります。全体として、あまり相関はなさそうですが、局所に右肩上がりの直線上に分布している箇所が見られます。少し謎です。

同じデータを用いて、確実圏偏差値に対する20%幅のヒストグラムを作ると、このようになります。

オレンジの折れ線グラフを見ると、偏差値が上がると20%幅の平均値は下がる傾向がわかります。確実圏偏差値40〜50だと20%幅は6前後、偏差値50〜60だと20%幅は5前後、偏差値60を超えると20%幅は4くらいになるようです。
分布の分析の際には、確実圏偏差値で40〜50、50〜60、60〜70の3区分くらいで考えるのが良さそうだとわかりました。
2. 首都圏の主要高校の実質倍率
次に高校の実質倍率(合格者÷受験者)をチェックします。実質倍率は合格者と不合格者の分布に影響するので、合格判定偏差値における合格率に影響を与えます。
主要高校の実質倍率(2024年度)を調べると、このようになりました。早慶MARCH、私立進学校・その他附属、都立・国立附属の3つの表に整理しています。

どの表でも倍率3倍前後(2.5〜3.5倍)にボリュームがあることがわかります。早慶MARCHは4倍を超える当たりにも塊がある一方、都立高は1.5倍前後に塊があります。このことから、分布を分析する際の倍率は、3.0倍を基本として、1.5倍と4.5倍も見るのが良さそうです。
3. 基本の合否分布モデルの作成
これまでの分析では難関高校を扱ってきたので、確実圏偏差値60を基本モデルで採用します。また、基本モデルの倍率は3.0倍とします。そのどちらにも該当する高校を、前後の幅を持って抽出すると、明大明治、立教新座、青山学院、お茶大附属、東京学芸大附属などになります。
合否分布を作成するにあたり、他にもいくつか数字の設定が必要です。上記の駿台中学生テストの分析や合否追跡データの分布形状も参考にして、以下のように設定します。
定員:100人
確実圏と可能圏の差(20%幅):4.0
合格と不合格のピークの差:6.0
合格者と不合格者のそれぞれの分布幅:29
合格者と不合格者の分布の標準偏差:5.0
分布は相対値なので、最初の定員はどんな数字でもいいのですが、イメージしやすいように、100人としました。上記の設定値とは別にアナログに調整している数字として、合格者平均偏差値があります。合格者平均偏差値は、倍率3倍の時に確実圏の合格者比率が80%前後、可能圏の合格者比率60%前後なる位置で調整しています。
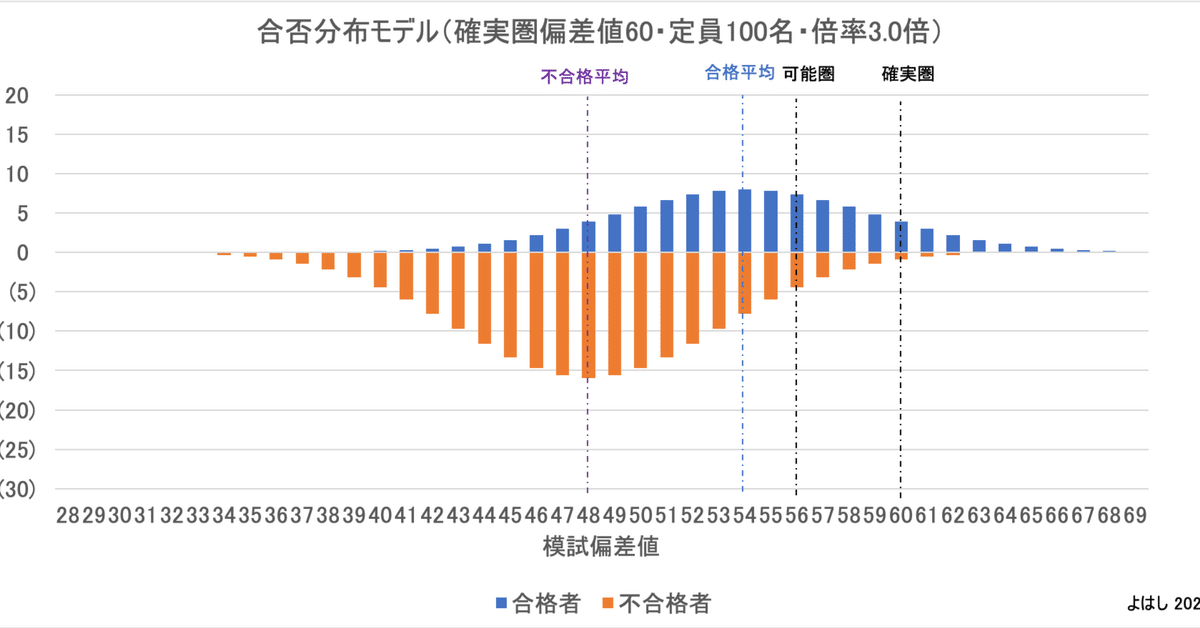
これらの設定値を用いて、合格者と不合格者がどちらも正規分布するという前提の元で、模試の偏差値に対する合否の分布を計算するとこのようになります。

グリーンが確実圏偏差値(60)で合格者比率は81%、黄色が可能圏偏差値(56)で合格者比率は62%です。ブルー(54)が合格者平均偏差値で、合格者のピークに当たります。同様にオレンジ(48)が不合格者平均偏差値で、不合格者のピークになります。グレーが受験者の平均偏差値です。
また右から2列目の受験者累計が定員100人を超えるところが、赤文字のところになります。これが最低合格ライン(ボーダー)になります。厳密には模試偏差値ではなく、当日偏差値で評価すべきなのですが、詳細は後日検討するとして、ここでは単純に模試偏差値で上からカウントして、定員を超える偏差値53をボーダーと見なします。
この関係を逆に捉えると、「確実圏偏差値が60で合格率80%、可能圏偏差値が56で合格率60%の高校において、倍率が3倍の時には、合格者平均偏差値は54、不合格者平均偏差値は48となる。そして、この場合には受験当日のボーダーにあたる偏差値は53」と言えます。
合否の分布をグラフにするとこんな感じです。なんかいい感じの分布の印象です。

受験者全体の分布と上位からの累計人数もグラフにしてみました。

受験者全体の分布は正規分布に近いので、悪くない感じです。一説では「受験者の分布は正規分布でなく、ワイブル分布になる」とも言われているようなので、正規分布だからいい分布というわけではないですが、よく見る受験者分布に近いので、良しとします。
4. 他の確実圏偏差値・倍率での合否分布
上記は確実圏偏差値60・倍率3.0倍の合否分布モデルでした。ここで、確実圏偏差値と倍率を変えてみたらどうなるか見てみます。他の偏差値・倍率でも、基本モデルと同じ考え方でシミュレーションしています。
個々の計算の説明は省略して一覧にすると、こうなります。

表を眺めると、以下の傾向が確認できます。
ボーダー偏差値は、確実圏偏差値のマイナス7〜10に存在する。
同じ確実圏偏差値なら、倍率が高くなると、合格者割合(=合格可能性)は下がる。
後者の傾向は、低倍率よりも高倍率の方が近い学力の受験生が多いことで変動性が高まると考えると、妥当なように思います。本来なら倍率に応じて確実圏偏差値を変えるべきなのですが、そもそも80%という設定は倍率1.25倍で全員が確実圏(A判定)となるので、限界があるのだと考えます。
いくつかの合否分布グラフも並べてみます。まずは、同じ確実圏偏差値60で倍率を変えています。



次に、同じ倍率で確実圏偏差値を変えた場合です。


5. 最後に
受験の合否分布のモデルを作って分析したところ、駿台中学生テストの確実圏偏差値60の高校は、倍率3倍であれば、最下位合格ラインは偏差値53という結果が出ました。これは、明大明治、立教新座、青山学院、お茶大附属、東京学芸大附属には、駿台中学生テストの偏差値53を超えれば合格できる、ということを意味します。
このボーダーのイメージは、winningticket-2025さんのブログの見立てとも一致します。おそらく、私も見たことがあるネットに出ていた合否追跡データをご覧になっているのではないかと思います。
それでは、「駿台中学生テストの確実圏偏差値60の高校は、倍率3倍であれば、最下位合格ラインは偏差値53」という分析結果が妥当であるとして、持ち偏差値が50の受験生がこの高校に合格できる可能性はどう考えたらいいのでしょうか? 単純に合否分布から計算される合格率(28%)と考えていいのでしょうか?
次はこの分析に取り組みたいと思います
この記事が気に入ったらサポートをしてみませんか?
