2022年 名古屋市立大学 前期 経済 大問2

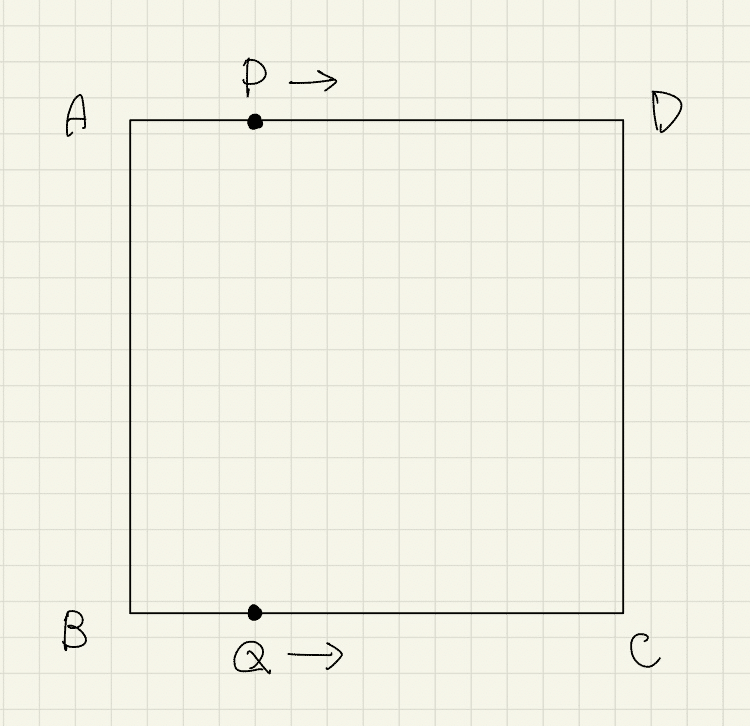
図のように1辺の長さが1の正方形$${ABCD}$$がある. また, 硬貨を投げて, 表ならば2, 裏ならば1だけ, この正方形の辺上を動く点$${P,Q}$$を考える. 点$${P}$$は, 頂点$${A}$$を出発点とし, 時計回りに動く. 点$${Q}$$は, 頂点$${B}$$を出発点とし, 反時計回りに動く. はじめに硬貨を10回投げて点$${P}$$のみを動かしたあと, さらに硬貨を10回投げて点$${Q}$$のみを動かすとき, 次の問いに答えよ.
(1) 点$${P}$$を動かし終わったあとに, 点$${P}$$が頂点$${A,B,C,D}$$にある確率をそれぞれ求めよ.
(2) 点$${P,Q}$$を動かし終わったあとに, 点$${P}$$と点$${Q}$$が異なる頂点にある確率を求めよ.

解答
(1) A1/4 B15/64 C1/4 D 17/64
(2) 3/4

(1)
硬貨を$${10}$$回投げた後に移動した総距離は$${10}$$から$${20}$$の整数をとる.
ここで, 総距離が$${10}$$となる確率を$${P(10)}$$のように表すとする.
総距離が$${10}$$となるのは, $${10}$$回すべて裏であるときだから,
$${P(10)={}_{10}C_{0}(\frac{1}{2})^{10}=\frac{1}{2^{10}}}$$となる.
また, 総距離が$${11}$$となるのは, 表が$${1}$$回, 裏が$${9}$$回のときだから,
$${P(11)={}_{10}C_1(\frac{1}{2})^9(\frac{1}{2})=\frac{10}{2^{10}}}$$となる.
以下同様に考えると,
$${P(12)={}_{10}C_2(\frac{1}{2})^8(\frac{1}{2})^2=\frac{45}{2^{10}}}$$,
$${P(13)={}_{10}C_3(\frac{1}{2})^7(\frac{1}{2})^3=\frac{120}{2^{10}}}$$,
$${P(14)={}_{10}C_4(\frac{1}{2})^6(\frac{1}{2})^4=\frac{210}{2^{10}}}$$,
$${P(15)={}_{10}C_5(\frac{1}{2})^5(\frac{1}{2})^5=\frac{252}{2^{10}}}$$,
$${P(16)={}_{10}C_6(\frac{1}{2})^4(\frac{1}{2})^6=\frac{210}{2^{10}}}$$,
$${P(17)={}_{10}C_7(\frac{1}{2})^3(\frac{1}{2})^7=\frac{120}{2^{10}}}$$,
$${P(18)={}_{10}C_8(\frac{1}{2})^2(\frac{1}{2})^8=\frac{45}{2^{10}}}$$,
$${P(19)={}_{10}C_9(\frac{1}{2})^1(\frac{1}{2})^9=\frac{10}{2^{10}}}$$,
$${P(20)={}_{10}C_{10}(\frac{1}{2})^{10}=\frac{1}{2^{10}}}$$
となる.
移動後点$${P}$$が頂点$${A}$$にあるのは, 総距離が$${12,16,20}$$のときであるから, これを$${P(A)}$$のように表すと
$${P(A)=P(12)+P(16)+P(20)=\frac{45+210+1}{2^{10}}=\frac{256}{2^{10}}=\dfrac{1}{4}}$$である.
$${B}$$以降も同様に考えて,
$${P(B)=P(11)+P(15)+P(19)=\frac{10+252+10}{2^{10}}=\frac{272}{2^{10}}=\dfrac{17}{64}}$$
$${P(C)=P(10)+P(14)+P(18)=\frac{1+210+45}{2^{10}}=\frac{256}{2^{10}}=\dfrac{1}{4}}$$
$${P(D)=P(13)+P(17)=\frac{120+120}{2^{10}}=\frac{240}{2^{10}}=\dfrac{15}{64}}$$
である.

(2)
点$${P}$$と点$${Q}$$の動きは対称だから, 移動後に点$${P}$$が$${A}$$にある確率を$${Q(A)}$$と表すと, (1)を用いて
$${Q(A)=P(B)=\frac{17}{64}}$$となる. 他の頂点も同様に考えて,
$${Q(B)=P(A)=\frac{1}{4}}$$, $${Q(C)=P(D)=\frac{15}{64}}$$, $${Q(D)=P(C)=\frac{1}{4}}$$となる.
いま, 余事象である「移動後に点$${P}$$と点$${Q}$$が同じ頂点にある」確率を考える.
点$${P}$$と点$${Q}$$が共に頂点$${A}$$にある確率を$${R(A)}$$と表すと,
$${R(A)=P(A)Q(A)=\frac{1}{4}\times{\frac{17}{64}}}$$
同様に,
$${R(B)=P(B)Q(B)=\frac{17}{64}\times{\frac{1}{4}}}$$
$${R(C)=P(C)Q(C)=\frac{1}{4}\times{\frac{15}{64}}}$$
$${R(D)=P(D)Q(D)=\frac{15}{64}\times{\frac{1}{4}}}$$
となるから, この確率は
$${\frac{17+17+15+15}{4\times{64}}=\frac{1}{4}}$$
である.
したがって, 求める確率は
$${1-\frac{1}{4}= \dfrac{3}{4}}$$である.