t検定でのサンプルサイズと効果量と検出力の関係

はじめに

統計的な検定について、検定の結果は効果量、有意水準、検出力、サンプルサイズの4つ要素によって変わるので、事前に効果量、有意水準(通常0.05)、検出力(通常0.8)を設定してサンプルサイズ設計をするのが望ましいですが（t検定やサンプルサイズ設計の話は今回は割愛）、実際観測データを扱う場合は既に十分多いサンプルがそろっている場合がありますね。
その場合検出力がほぼ1になり有意な結果になると予想されますが、解釈を深めるために、実際にサンプルサイズや効果量がどのくらいの数字だったら検出力がどうなるのかを知りたいと思い、パラメータが多いからか調べても全然出てこなかったので、自分で計算してみようと思いました。

検定内容

検定によって効果量や検出力は変わりますが、今回は簡単な対応のない2群のt検定で行います。2群は等分散を仮定して、効果量は不変分散を用いてプールさせた標準偏差を使うhedge's g （平均/標準偏差）を使います。
hedge's gの式参考
31-3. 効果量2 | 統計学の時間 | 統計WEB (bellcurve.jp)

データ

感覚つかむためにはランダムデータよりも実際のデータがよいかなと思い使えそうなデータ探しましたが、ちょうどいい大量のローデータは見つからなかったので、下記リンクのサンプリングされた男女の身長のデータを使うことにしました。
2019年の30歳-39歳のデータで男女の身長差を考えます。
【男性】人数：178、平均値：171.5、標準偏差：5.5
【女性】人数：225、平均値：158.2、標準偏差：5.5

国民健康・栄養調査14 身長・体重の平均値及び標準偏差 - 年齢階級，身長・体重別，人数，平均値，標準偏差 - 男性・女性，１歳以上〔体重は妊婦除外〕 | 統計表・グラフ表示 | 政府統計の総合窓口 (e-stat.go.jp)

検定

Pythonを使って計算します。

import statsmodels.stats.power as smp
import matplotlib.pyplot as plt
import numpy as np

#分散
var_m = std_m**2
var_f = std_f**2

#不偏分散
uvar_m = var_m*n_m/(n_m-1)
uvar_f = var_f*n_f/(n_f-1)

#プールした分散と標準偏差（hedge's g用)
s2_pool_g = ((n_m-1)*uvar_m+(n_f-1)*uvar_f)/(n_m+n_f-2)
s_pool_g = np.sqrt(s2_pool_g)

#平均の差の分布の標準偏差
dif_std = s_pool_g*np.sqrt((1/n_m)+(1/n_f))

#観測された平均の差
dif_ave = ave_m - ave_f

#t値
t = dif_ave/dif_std

#自由度
dof = n_m+n_f-2

# 効果量 (hedge's g)
effect_size = dif_ave / s_pool_g

# 検出力（検出力は関数の力を借ります）
# レシオ      
ratio = n_f/n_m
# 両側検定か、片側検定か、'two-sided' (default), 'larger', 'smaller'　指定
alternative ='larger'
# 有意水準
sig = 0.05
# 検出力
p= smp.TTestIndPower().power(effect_size=effect_size, nobs1=n_m, ratio=ratio, alpha=sig, alternative=alternative)

print('t値:',t)
print('自由度:',dof)
print('効果量:',effect_size)
print('検出力:',p)

出力
t値: 24.04680335159937
自由度: 401
効果量: 2.4121739037608196
検出力: 1.0

普通にt検定をすると結果t値は24.0と非常に大きく、有意差があります。
hedge's gは0.2を小さい効果、0.5を中程度の効果、0.8を大きい効果といわれていますので、効果量も高く、検出力も1と高いです。
男女に身長差があるのは感覚通りでしたが、これだけだとサンプルサイズと効果量の関係が見えてこないので条件を振って確認していきます。

サンプルサイズとt値の関係

サンプルサイズ設計の話ではサンプルサイズは大きくすればするほど有意差ありになりやすくなるから設計必要といわれており、それは平均の差の分布の標準偏差のsqrt((1/n_m)+(1/n_f))の部分が小さくなるのが主に効いていて、t値が大きくなるということになりますが、実際どのような数値感なのでしょうか、確認します。簡単のために2群のサンプル数は同じにします。

 #効果量 
effect_size_list = [0.1,0.3,0.5,0.8,1,2]
#サンプル数(# n_mとn_f同じとする)
n = np.linspace(10, 200, 100)
#プロット
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_yticks(np.arange(0, 20, step=2))
ax.set_xticks(np.arange(0, 200, step=10))
for i in effect_size_list:
    #t値
    t= i/np.sqrt((1/n)+(1/n))
    plt.plot(n, t, label=f"effect_size:{i}")
    plt.legend()
    plt.xlabel("sample_size")
    plt.ylabel("t_value")
    plt.xticks(rotation=90)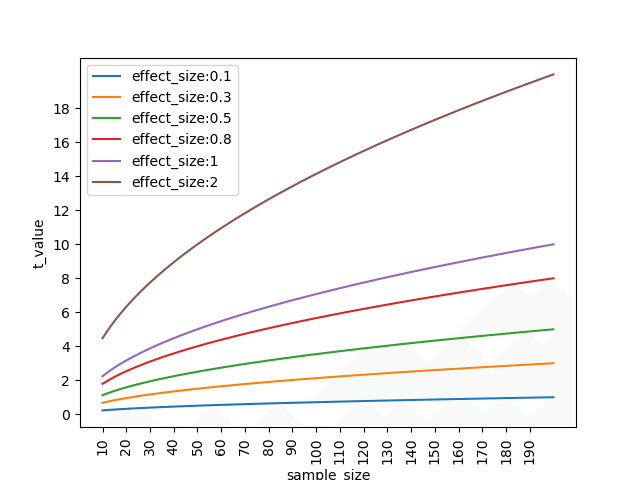

サンプルサイズが大きくなればt値が大きくなっていくのが可視化できました。
自由度によって有意水準5%のt値は変わりますが、自由度増えてくるとだいたい2.0くらいで5%なので参考にそのあたりでみてみると効果量0.3でサンプル数90程、効果量0.5で30程、効果量0.8で15程、効果量1.0以上はサンプルもっと少なくても有意差でるような感じですね。

サンプルサイズと検出力と効果量の関係

 #効果量 
effect_size_list = [0.1,0.3,0.5,0.8,1,2]
#サンプル数
n = np.linspace(10, 200, 100)
#プロット
fig = plt.figure()
ax = fig.add_subplot(111)
for i in effect_size_list:
     #検出力     
    p= smp.TTestIndPower().power(effect_size=i, nobs1=n, ratio=1, alpha=0.05, alternative='larger')
    plt.plot(n, p, label=f"effect_size:{i}")
    plt.legend()
    plt.xlabel("sample_size")
    plt.ylabel("power")

サンプルサイズが大きいほど検出力が高くなり、効果量も大きいものほど検出力が高いのが可視化できました。
効果量が高いと言われる1以上ではサンプルがかなり少なくても検出力が0.8より高くなっていますね。

検出力を0.8に固定

最後に検出力がちょうど0.8になるところのサンプルサイズでt値と一緒にプロットしてみます。

 #効果量 
effect_size_list = [0.1,0.3,0.5,0.8,1,2]
#プロット
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_xticks(np.arange(0, 1250, step=50))
for i in effect_size_list:
    #t値
    n=smp.tt_ind_solve_power(ratio =1 , effect_size=i, alpha=sig, alternative='larger', power=0.8)
    t= i/np.sqrt((1/n)+(1/n))
    plt.plot(n, t, label=f"effect_size:{i},n:{n}", marker='o')
    plt.legend()
    plt.xlabel("sample_size")
    plt.ylabel("t_value")
    plt.xticks(rotation=90)

プロットしてみて気づきましたが検出力が0.8になるくらいの帰無仮説と対立仮設の分布の距離と裾の広がり方の関係なら有意差5%なら基本的に有意差ありになるようですね。考えてみれば確かにそうですが。それぐらいの関係で有意差ありを導きなさいということですね。

まとめ

観測データで検定を解釈する際には、効果量を見ずに有意差ありと判断したときにはどのくらいの差があるのかが判断できないので絶対に効果量は見た方がよく、効果量が高い場合はサンプル少なくてもどうせ有意差ありになり検出力も高くなるので素直に差があると解釈して良さそう。
効果量が小さいか中くらいの場合は検出力を見て0.8より大きいか小さいかを見てサンプル数が大きすぎて有意差ありになっているかもしれないとか、サンプル数が少なすぎて有意差が出ていないだけかもしれないといった解釈を加えれば良さそう。

さいごに

以上、似たような疑問を抱えていた方に少しでもご参考になれば幸いです。