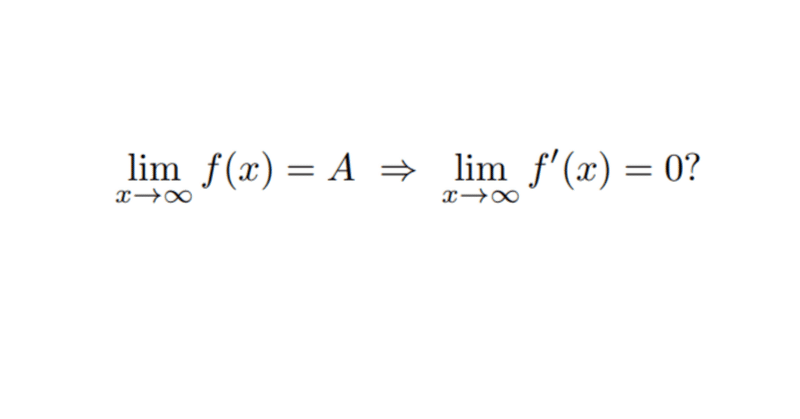
f(x)→A(x→∞)ならばf'(x)→0か？

ここでは

ある区間$${(a,+\infty)}$$上$${C^1}$$級関数$${f}$$について,極限値$${\displaystyle\lim_{x\to\infty}f(x)}$$が存在するならば$${\displaystyle\lim_{x\to\infty}f'(x)=0}$$か？

ということを考えます。ある1つの値に収束するならその変化率も小さくなっていきそうで、直観的には正しそうですが、実は正しくありません。つまり$${x\to\infty}$$でえぐい振動をしながら収束するような関数があるからです。反例としては

                       $${f(x)=e^{-x^2}\sin e^{x^2}}$$

があります。この関数は$${C^{\infty}}$$級で、$${\displaystyle\lim_{x\to\infty}f(x)=0}$$と収束しますが、

                $${f'(x)=2x\cos e^{x^2}-2xe^{-x^2}\sin e^{x^2}}$$

なので、最初の項が振動し、第二項は$${0}$$に収束するため$${f'(x)}$$は発散してしまいます。

いろいろ条件を課してみる

$${f'}$$に他に条件をつけ足したときの結論をいくつか紹介します。

1.極限値$${\displaystyle\lim_{x\to\infty}f'(x)}$$の存在
最も簡単なのは$${f'(x)}$$の収束を仮定してしまうことです。このとき平均値の定理により、任意の$${n\in\mathbb{N}\cap(a,\infty)}$$対して

                              $${f(n+1)-f(n)=f'(c_n)}$$

となる$${c_n\in(n,n+1)}$$が存在します。この数列$${(c_n)}$$は正の無限大に発散し、

　　　　$${\displaystyle\lim_{n\to\infty}f'(c_n)=\displaystyle\lim_{n\to\infty}(f(n+1)-f(n))=A-A=0}$$

となりますが、今極限値$${\displaystyle\lim_{x\to\infty}f'(x)}$$の存在が仮定されているので、極限の一意性によって$${\displaystyle\lim_{x\to\infty}f'(x)=0}$$を得ます。

2.$${f'}$$が有界
これには反例があり、$${f(x)=\dfrac{\sin x^2}{x}(x\in(0,\infty))}$$が該当します。$${\displaystyle\lim_{x\to\infty}f(x)=0}$$で、また

        $${f'(x)=2\cos x^2-\dfrac{\sin x^2}{x^2}}$$

で第一項、第二項ともに$${(0,\infty)}$$で有界なので$${f'}$$は有界です。しかし$${f'}$$は$${x\to\infty}$$で振動します。

3.$${f'}$$の一様連続性(Barbalat's lemma)
最後は$${f'}$$に一様連続性を課します。これはBarbalat's lemmaと呼ばれ、肯定的な結論が得られることが知られています。

この証明には背理法を用います。すなわち、$${\displaystyle\lim_{x\to\infty}f'(x)=0}$$でないとすると、これは

           $${\exists\varepsilon>0,\forall M>a,\exists x (x>M}$$かつ$${|f'(x)|\geq\varepsilon)}$$

と同等です。したがって有界でないある狭義単調増加数列$${(x_n)}$$が存在して、$${|f'(x_n)|\geq\varepsilon}$$となります。また$${f'}$$の一様連続性によって、ある$${\delta>0}$$が存在して

　　$${|x-x_n|\leq\delta  \Rightarrow   |f'(x)-f'(x_n)|\leq\dfrac{\varepsilon}{2}}$$.

よって任意の$${n\in\mathbb{N}}$$と任意の$${x\in[x_n,x_n+\delta]}$$において

$${|f'(x)|=|f'(x_n)-(f'(x_n)-f'(x))|\geq |f'(x_n)|-|f'(x_n)-f'(x)|\geq\varepsilon-\dfrac{\varepsilon}{2}=\dfrac{\varepsilon}{2}}$$.

区間$${[x_n,x_n+\delta]}$$において$${f'}$$の正負は変わらないことに注意します。もし正負が変わってしまえば、$${f'}$$は連続ゆえ中間値の定理からこの区間内の点$${a}$$で$${f'(a)=0}$$となるものが存在してしまい、いま導いた不等式と矛盾するからです。よって

 $${\left|\displaystyle\int_{x_n}^{x_n+\delta}f'(x)dx\right|=\displaystyle\int_{x_n}^{x_n+\delta}|f'(x)|dx\geq\dfrac{\varepsilon\delta}{2}>0}$$

となり、$${\displaystyle\int_a^{\infty}f'(x)dx}$$は発散します。これは$${f(x)=\displaystyle\int_a^{x}f'(t)dt+f(a)}$$が$${0}$$に収束することに矛盾します。(記号が重複しますが$${a}$$を定義域内の点とします。)これで証明は完了しました。

この証明は次の記事をもとにしています。

proof of Barbalat’s lemma

おわりに

急いで書いたので(言い訳)、何か間違いがありましたらコメント等をお願いします。お読みいただきありがとうございました。