
Radiomics超入門:Gray Level Co-occurence Matrix特徴
概要
テクスチャに関する特徴は従来、2D 画像の表面のテクスチャを評価するために設計されていました。しかし、近年では、テクスチャ解析は 2D 画像に限定されるものではなくなり、3D オブジェクトにも拡張可能になっています。
GLCMの計算に用いる画像の信号強度は、一般的に、GLCMを計算する前に離散化されます。
Gray Level Co-occurence Matrix(GLCM)は、テクスチャを表現する特徴の一つです。
どのように信号強度がペアで並んでいるかを、角度と距離を決めたうえで探索して、実際に見つかったペア (Joint) の数をマトリクスにカウントしていきます。この結果得られたマトリクスは、隣接するピクセルの離散化された信号強度(グレーレベル)の組み合わせが、画像の中でどのように分布しているかを表す行列になります。
例えば、下の図では、グレーレベル「1」とグレーレベル「2」のペアを探索する例を示しています。GLCMの行と列は、グレーレベルに対応します。ここで、左側「1」右側「2」となっているペアは、この例では2つしかありません。よって、GLCMの行「1」列「2」の位置に、カウント数である 2 が当てはめられることになります。このように、すべての組み合わせを数えて、マトリクスを埋めていったものがGLCMです。
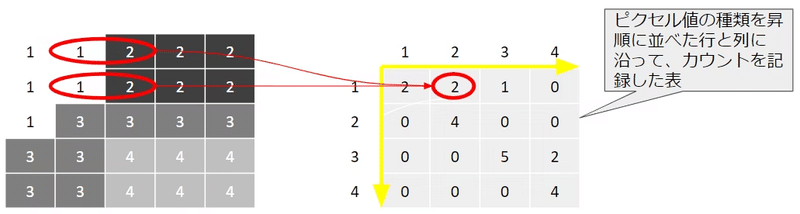
(左:5×5 ピクセルからなる画像、右:GLCM,ただし、探索角度は 0 °、距離は 1 。)
ただし、探索する際は、探索方向となる角度と、Joint するボクセルの距離(オフセット)を指定する必要があります。オフセットは、何個飛ばしで探すか(1のときは隣り合わせ)です。オフセットは 1 が汎用されます。
探索方向については、2Dで用いられる探索角度は 4 方向(0°、45°、90°、135°)です。これらを方向ベクトル$${(x,y,z)}$$で表すと、次のようになります。
$$
(1,0,0), (1,1,0), (0,1,0), (-1,1,0)
$$

(シンメトリーを前提にした場合)
2D の場合にベクトルは4方向しかない理由については後述しますが、ここでは簡単に、対方向からのGLCMは一方のGLCMの鏡像になるため、パターン化という観点からみれば、同じことをやっていることになるためです。
3D の場合は、13 のユニークな方向ベクトルが存在することになります。26方向でない理由は、2D が 4 方向ベクトルしかないことと同じ理由です。
$$
(0,0,1) \\
(0,1,0) \\
(1,0,0) \\
(0,1,1) \\
(0,1,-1) \\
(1,0,1) \\
(1,0,-1) \\
(1,1,0) \\
(1,-1,0) \\
(1,1,1) \\
(1,1,-1) \\
(1,-1,1) \\
(1,-1,-1)
$$
Joint を計算するための近傍領域(Joint するボクセルのペアを探す領域)は、チェビシェフ距離 $${δ=1}$$を探索距離とした場合、3D では 26 近傍領域、2D では 8 近傍領域です。
GLCMは各方向ベクトルに対して計算されます。
$${M_m}$$ を$${ Ng×Ng}$$ なGLCMの行列とします。$${{N_g}$$は ROI 信号強度マスク上の離散化されたグレーレベルの数、$${m}$$ は特定の方向ベクトルを意味します。
GLCMの要素$${(i,j)}$$は、グレーレベル$${i}$$ と$${j}$$ がペアになった頻度です。
具体的なGLCMの計算例を以下に示します。

(b) GLCM θ=0° δ=1 方向ベクトル (1,0)
(c) GLCM θ=180° δ=1 方向ベクトル (-1,0)
(探索方向が真逆になると、鏡像になっている。対称(シンメトリー)なマトリクスにするには、これらを足し合わせる。)
Addapted from IBSI reference Fig.10
ここで、(b) と (c) は、角度方向が真逆になっており、それぞれのマトリクスが鏡像になっていることがわかります。これは、テクスチャのパターンを分けるという観点から考えると、同じことを二度やってしまっているとも考えられますから、一般に、GLCMはこれらを足し合わせて、対称(シンメトリー)なGLCMとして扱われます。
以下は、シンメトリーなGLCMを前提に計算した各方向でのマトリクスです。

(m=(1,0):0° , m=(1,1):45° , m=(0,1):90°, m=(−1,1):135°)
Addapted from IBSI reference Fig.11
GLCMの確率分布
GLCM 特徴は、GLCM の要素の確率分布から計算されます。下図の$${M_m=(1,0)}$$の例(0°方向ベクトルの探索で得られたGLCM)で考えてみます。

(b) 対応する確率行列 Pm=(1,0)と周辺確率 pi.および p.j
(c) 対角確率 p i-j
(d) 十字対角確率 p i+j
※シンメトリーなGLCMを前提にしているため、a, bの行と列の両方において、周辺確率 pi.とp.jが同じになっている。
※小数点第二位の丸め誤差により多少数値が変わる
Addapted from IBSI reference Fig.12
ある方向ベクトル$${m}$$で得られたGLCMの確率分布$${P_m}$$は、$${M_m}$$をその要素の和で正規化することにより算出されます。$${P_m}$$の各要素$${p_{ij}}$$は、グレーレベル$${i}$$と$${j}$$が方向ベクトル$${m}$$に沿って隣接する確率を表します。
このとき、$${p_{i.} = \sum_{j=1}^{N_g} p_{ij}}$$は行に対する周辺確率であり、$${p_{.j} = \sum_{i=1}^{N_g} p_{ij}}$$は列に対する周辺確率です。
$${P_m}$$は定義上対称となるため、$${p_{i.}=p_{.j}}$$となります。
さらに、対角確率$${p_{i-j}}$$と十字対角確率$${p_{i+j}}$$は次のとおりです [Haralick1973][Unser1986]。
$$
p_{i-j,k} = \sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p_{ij} { }[k=\lvert i-j \rvert] { } k=0,…,N_g-1
$$
$$
p_{i+j,k} = \sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p_{ij} { }[k=i+j] { } k=2,…,2N_g
$$
ここで、[...]はアイバーソン条件式です。条件が成立する要素$${(i,j)}$$ の組み合わせのみが計算されます。
GLCMでは探索する距離として$${δ=1}$$ が一般的に用いられますが、他の距離も設定可能です。例えば、$${δ=3}$$の3Dの場合、ボクセル中心から、(0,0,3), (0,3,0),(3,0,0), (0,3,3), (0,3,-3), (3,0,3), (3,0,-3), (3,3,0), (3,-3,0), (3,3,3), (3,3,-3), (3,-3,3)および(3,-3,-3)にあるボクセルが Joint として計算されることになります。
特徴の集約
回転不変性(rotational invariance)を向上させるために、GLCM 特徴値は、複数の方向ベクトル$${\delta}$$からの結果を集約することによって計算されます[Depeursinge2017a]。
複数のGLCMを集約して特徴値を得るには、6 つの方法があります。

Addapted from IBSI reference Fig.13
$${M_{∆k}}$$は、画像スライス$${k}$$における探索方向$${δ}$$について計算されたテクスチャ行列、$${f_{δk}}$$は対応する特徴量です。
(a) 各 2D 画像スライスから、$${\delta}$$分だけマトリクスを計算し、特徴を計算して、平均化する方法。
(b) 各 2D 画像スライスから、$${\delta}$$分だけマトリクスを計算し、マトリクスをスライスごとにマージした後、特徴量を計算してから、平均化する方法。
(c) 探索方向$${\delta}$$ごとに行列をマージした後、$${\delta}$$ごとに特徴を計算し、平均化する方法。
(d) すべての画像スライスにおける各$${\delta}$$でのマトリクスをマージした後、特徴量を計算する方法。
(e) 3次元の探索方向$${\delta}$$ごとにマトリクスを計算し、特徴を算出した後に平均化する方法。
(f) 3次元の探索方向$${\delta}$$でマトリクスを得た後、マトリクスをマージし、特徴量を計算する方法。
(b) ~ (d)と(f)では、各 GLCM 要素$${(i,j)}$$の共起カウントを合計した行列(マージされた行列)が作成され、マージされた GLCM から特徴が計算されます。
特徴量は、集約方法に強く依存する可能性があります。
Distances and distance weighting(探索距離と距離重み)
GLCMはそれ自身であるマトリクス$${M}$$に重み付け係数$${w}$$を乗算することで距離による重み付けを行うことができます。
一般的には、$${w=1}$$ですが、$${w}$$は各GLCMを重み付けする逆距離関数を用いることもできます。
例えば、$${w = { \| m \| }^{-1}}$$または$${w=exp(- { \| m \| }^2)}$$ などです[VanGriethuysen2017]。$${ \| m \|}$$は方向ベクトル $${m}$$の長さです。
距離による重み付けによって異なる特徴値が得られるかどうかは、いくつかの要因に依存します。
特徴値を集約する場合には特に、GLCMは最初にマージされる必要があります。そうでなければ重み付けによる影響が無くなるためです。また、デフォルトの近傍領域(1)を使用し、重み付けにチェビシェフ・ノルムを使用した場合も重み付けは効果がありません($${w=1}$$のため)。次に、マンハッタン・ノルムまたはチェビシェフ・ノルムのどちらかが、デフォルト(1)の近傍領域でない近傍領域の決定と重み付けの両方に使用される場合にも、重み付けは効果を持ちません。
これらの例外のため、IBSIではGLCMに距離重み付けを使用しないことを推奨しています。
GLCM特徴
Joint maximum
Joint maximum は、GLCMで最も高いグレーレベルの共起に対応する確率です。
$$
F_{cm.joint.max}=max(p_{ij})
$$
Joint average
Joint average は、グレーレベルで重み付けされた共起確率の総和です。
$$
F_{cm.joint.avg}=\displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_g} {ip_{ij}}
$$
Joint variance
Joint variance は、sum of squares [Haralick1973] とも呼ばれます。次のように定義されます。
$$
F_{cm.joint.var}=\displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_g} {(i-\mu)^2}{p_{ij}}
$$
ここで、$${\mu}$$は$${F_{cm.joint.avg}}$$です。
Joint entropy
Joint entropy は次のように定義されます。
$$
F_{cm.joint.entr}= -\displaystyle\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p_{ij}\log_2{p_{ij}}
$$
Difference average
Difference average は、対角確率から計算されます。
$$
F_{cm.diff.avg}= \displaystyle\sum_{k=0}^{N_g-1} k p_{i-j,k}
$$
別名でdissimilarity [VanGriethuysen2017]とも呼ばれます。
Difference variance
Difference variance は、対角確率から計算されます。
$$
F_{cm.diff.var}= \displaystyle\sum_{k=0}^{N_g-1} (k-\mu)^2 p_{i-j,k}
$$
ここで、$${\mu}$$は$${F_{cm.diff.avg}}$$です。
Difference entropy
Difference entropy は、対角確率から計算されます。
$$
F_{cm.diff.entr}= - \displaystyle\sum_{k=0}^{N_g-1} p_{i-j,k} \log_2{p_{i-j,k}}
$$
Sum average
Sum average は十字対角確率から求められます。
$$
F_{cm.sum.avg}= \displaystyle\sum_{k=2}^{2N_g} k p_{i+j,k}
$$
ここで、$${F_{cm.sum.avg}=2F_{cm.joint.avg}}$$です。
Sum variance
Sum varianceは十字対角確率から求められます。
$$
F_{cm.sum.var}= \displaystyle\sum_{k=2}^{2N_g} (k-\mu)^2 p_{i+j,k}
$$
ここで、$${\mu=F_{cm.sum.avg}}$$です。
また、Sum varianceは、数式上、Cluster Tendencyと同じ意味を持つ特徴です。
Sum entropy
Sum entropyは十字対角確率から求められます。
$$
F_{cm.sum.entr}= -\displaystyle\sum_{k=2}^{2N_g} p_{i+j,k} \log_2 p_{i+j,k}
$$
Angular second moment
Angular second moment は、次のように求められます。
$$
F_{cm.energy}= \displaystyle\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p_{ij}^2
$$
この特徴は、energy [Unser1986]または、uniformity [Clausi2002]としても知られています。
Contrast
Contrast はグレーレベルの変化を評価する指標です。したがって、$${M_Δ}$$ (マトリクス間の差)の要素は、大きなグレーレベルの違いを表すものほど大きな重みを持ちます。Contrastは次のように定義されます。
$$
F_{cm.contrast}= \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_g} (i-j)^2p_{ij}
$$
Dissimilarity
Dissimilarity (非類似度)は、概念的にはContrast特徴と似ており、次のように定義されます。
$$
F_{cm.dissimilarity}= \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_g} \lvert i-j \lvert p_{ij}
$$
定義上、Dissimilarityは Difference average特徴と同じです。
Inverse difference
Inverse differenceは同質性の尺度です。差が大きいグレーレベルの共起は重みが小さくなり、その結果、特徴量の合計値が下がります。すべてのグレーレベルが同じ場合、最大となります。
次のように定義されます。
$$
F_{cm.inv.diff}= \displaystyle\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} \frac {p_{ij}} {1+\lvert i-j \lvert}
$$
上の式は対角確率で表すこともできます。
$$
F_{cm.inv.diff}= \displaystyle\sum_{k=0}^{N_g-1} \frac {p_{i-j,k}} {1+k}
$$
Normalised inverse difference
分類能力を向上させるためにInverse differenceを正規化した特徴です。次のように定義されます。
$$
F_{cm.inv.diff.norm}= \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_g} \frac {p_{ij}} {1+\lvert i-j \lvert /N_g}
$$
上の式は対角確率で表すこともできます。
$$
F_{cm.inv.diff.norm}= \displaystyle\sum_{k=0}^{N_g-1} \frac {p_{i-j,k}} {1+k/N_g}
$$
Inverse difference moment
Inverse difference moment(逆差分モーメント)は、Inverse difference 特徴とコンセプトは似ていますが、対角から離れた要素の重みが小さくなる特徴があります。
$$
F_{cm.inv.diff.mom}= \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_g} \frac {p_{ij}} {1+ ( i-j )^2}
$$
上の式は対角確率で表すこともできます。
$$
F_{cm.inv.diff.mom}= \displaystyle\sum_{k=0}^{N_g-1} \frac {p_{i-j,k}} {1+k^2}
$$
Normalised inverse difference moment
以下のように定義されます。
$$
F_{cm.inv.diff.mom.norm}= \displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j=1}^{N_g} \frac {p_{ij}} {1+ ( i-j )^2/N_g^2}
$$
上の式は対角確率で表すこともできます。
$$
F_{cm.inv.diff.mom.norm}= \displaystyle\sum_{k=0}^{N_g-1} \frac {p_{i-j,k}} {1+(k/N_g)^2}
$$
Inverse variance
Inverse variance(逆分散)は次のように定義されます。
$$
F_{cm.inv.var}= 2\displaystyle\sum_{i=1}^{N_g} \displaystyle\sum_{j>i}^{N_g} \frac {p_{ij}} {( i-j )^2}
$$
上の式は対角確率で表すこともできます。k=1からスタートする点に注意が必要です。
$$
F_{cm.inv.var}= \displaystyle\sum_{k=1}^{N_g-1} \frac {p_{i-j,k}} {k^2}
$$
Correlation
Correlation(相関)は次のように定義されます。
$$
F_{cm.corr}= \frac {1} {\sigma_{i.} \sigma{.j}} (-\mu_{i.} \mu_{.j} + \displaystyle\sum_{i=1}^{N_g}\displaystyle\sum_{j=1}^{N_g}ijp_{ij})
$$
$$
\mu_{i.} = \sum_{i=1}^{N_g}ip_{i.}
$$
$$
\sigma_{i.} = (\sum_{i=1}^{N_g} (i-\mu_{i.})^2p_{i.})^{1/2}
$$
$${\mu_{.j}}$$および$${\sigma_{.j}}$$も同様の方法で計算されます。
GLCMがシンメトリーの場合、この式は次のように簡単にできます。
$$
F_{cm.corr}= \frac {1} {\sigma_{i.}^2} (-\mu_{i.}^2 + \displaystyle\sum_{i=1}^{N_g}\displaystyle\sum_{j=1}^{N_g}ijp_{ij})
$$
式を変形するとこのようにも書けます。
$$
F_{cm.corr}= \frac {1} {\sigma_{i.} \sigma{.j}} \displaystyle\sum_{i=1}^{N_g}\displaystyle\sum_{j=1}^{N_g}(i-\mu_{i.})(j-\mu_{.j})p_{ij}
$$
これも同様に、シンメトリーの場合は簡略化できます。
$$
F_{cm.corr}= \frac {1} {\sigma_{i.}^2} \displaystyle\sum_{i=1}^{N_g}\displaystyle\sum_{j=1}^{N_g}(i-\mu_{i.})(j-\mu_{i.})p_{ij}
$$
Autocorrelation
[soh1999texture]らは、Autocorrelation(自己相関, 相互相関)を次のように定義しています。
$$
F_{cm.auto.corr}=\displaystyle\sum_{i=1}^{N_g}\displaystyle\sum_{j=1}^{N_g}ijp_{ij}
$$
Cluster tendency
Cluster tendency(クラスター傾向)は次のように定義されます。
$$
F_{cm.clust.tend}=\displaystyle\sum_{i=1}^{N_g}\displaystyle\sum_{j=1}^{N_g}(i+j-\mu_{i.} - \mu_{.j})^2p_{ij}
$$
ここで、各$${\mu}$$は次のように計算されます。
$$
\mu_{i.}=\sum_{i=1}^{N_g}ip_{i.}
$$
$$
\mu_{.j}=\sum_{j=1}^{N_g}jp_{j.}
$$
シンメトリーの場合、次のように簡略化できます。
$$
F_{cm.clust.tend}=\displaystyle\sum_{i=1}^{N_g}\displaystyle\sum_{j=1}^{N_g}(i+j-2\mu_{i.})^2p_{ij}
$$
Cluster tendencyは、数学的にはSum varianceと等しいです[VanGriethuysen2017]。
Cluster shade
Cluster shade は次のように定義されます。
$$
F_{cm.clust.shade}=\displaystyle\sum_{i=1}^{N_g}\displaystyle\sum_{j=1}^{N_g}(i+j-\mu_{i.}-\mu_{.j})^3p_{ij}
$$
ここで、各$${\mu}$$は次のように計算されます。
$$
\mu_{i.}=\sum_{i=1}^{N_g}ip_{i.}
$$
$$
\mu_{.j}=\sum_{j=1}^{N_g}jp_{j.}
$$
シンメトリーの場合、次のように簡略化できます。
$$
F_{cm.clust.shade}=\displaystyle\sum_{i=1}^{N_g}\displaystyle\sum_{j=1}^{N_g}(i+j-2\mu_{i.})^3p_{ij}
$$
Cluster prominence
Cluster prominence(クラスターの顕著性)は次のように定義されます。
$$
F_{cm.clust.prom}=\displaystyle\sum_{i=1}^{N_g}\displaystyle\sum_{j=1}^{N_g}(i+j-\mu_{i.}-\mu_{.j})^4p_{ij}
$$
ここで、各$${\mu}$$は次のように計算されます。
$$
\mu_{i.}=\sum_{i=1}^{N_g}ip_{i.}
$$
$$
\mu_{.j}=\sum_{j=1}^{N_g}jp_{j.}
$$
シンメトリーの場合、次のように簡略化できます。
$$
F_{cm.clust.prom}=\displaystyle\sum_{i=1}^{N_g}\displaystyle\sum_{j=1}^{N_g}(i+j-2\mu_{i.})^4p_{ij}
$$
Information correlation 1
Information correlation 1(情報理論的相関1)は2つの尺度を用いて推定されます。シンメトリーな場合は、次のように推定されます。
$$
F_{cm.info.corr.1}=\frac {HXY-HXY_1} {HX}
$$
HXYは、確率分布に対するEntropyです。
$$
HXY = - \sum_{i=1}^{N_g}\sum_{j=1}^{N_g}p_{ij}\log_2 p_{ij}
$$
HXは、行に対する周辺確率から計算されたEntropyです。
$$
HX = - \sum_{i=1}^{N_g}p_{i.}\log_2 p_{i.}
$$
$${HXY_1}$$は、列に対する周辺確率から計算されたEntropyです。
$$
HXY_1 = - \sum_{i=1}^{N_g}\sum_{j=1}^{N_g}p_{ij}\log_2 (p_{i.} p_{.j})
$$
Information correlation 2
Information correlation 2(情報理論的相関2)は、シンメトリーなGLCMの確率分布について、以下のように推定されます。
$$
F_{cm.info.corr.2} = \sqrt {1- \exp(-2(HXY_2-HXY))}
$$
HXYは、確率分布に対するEntropyです。
$$
HXY = - \sum_{i=1}^{N_g}\sum_{j=1}^{N_g}p_{ij}\log_2 p_{ij}
$$
$${HXY_2}$$は次のようなEntropyです。
$$
HXY_2 = - \sum_{i=1}^{N_g}\sum_{j=1}^{N_g}p_{i.}p_{.j}\log_2 (p_{i.} p_{.j})
$$
実践
RadiomicsJで、IBSIデジタルファントムからこれらの特徴を計算してみます。
GLCMの計算を確認する
先の例を使って、2D で 4 方向分の GLCM を計算してみます。
// create 2d array
byte pixels[] = new byte[16];
byte r0[] = new byte[] { 1, 2, 2, 3 };
byte r1[] = new byte[] { 1, 2, 3, 3 };
byte r2[] = new byte[] { 4, 2, 4, 1 };
byte r3[] = new byte[] { 4, 1, 2, 3 };
// flatten to create ByteProcessor
int i= 0;
for(byte[] r: new byte[][] {r0,r1,r2,r3}) {
for(byte v:r) {
pixels[i++] = v;
}
}
ImageProcessor bp = new ByteProcessor(4, 4, pixels);
ImagePlus imp = new ImagePlus("sample", bp);
int nBins = 4;// 1 to 4
int delta = 1;//distance
//init
GLCMFeatures test = null;
try {
test = new GLCMFeatures(imp, null, 1,delta, true, nBins, null, null);
} catch (Exception e) {
e.printStackTrace();
}
// angle new int[] {0,0,1} is ordered by z,y,x (dim2, dim1, dim0)
double[][] mat_0 = test.calcGLCM2(0, new int[] { 0, 0, 1 }, delta);
System.out.println("Check : (x,y,z)(1,0,0) vector →");
System.out.println(test.toString(mat_0));
double[][] mat_45 = test.calcGLCM2(0, new int[] { 0, 1, 1 }, delta);
System.out.println("Check : (x,y,z)(1,1,0) vector ↗");
System.out.println(test.toString(mat_45));
double[][] mat_90 = test.calcGLCM2(0, new int[] { 0, 1, 0 }, delta);
System.out.println("Check : (x,y,z)(0,1,0) vector ↑");
System.out.println(test.toString(mat_90));
double[][] mat_135 = test.calcGLCM2(0, new int[] { 0, 1, -1 }, delta);
System.out.println("Check : (x,y,z)(-1,1,0) vector ↖");
System.out.println(test.toString(mat_135));//出力
Check : (x,y,z)(1,0,0) vector →
0.000 3.000 0.000 2.000
3.000 2.000 3.000 2.000
0.000 3.000 2.000 0.000
2.000 2.000 0.000 0.000
Check : (x,y,z)(1,1,0) vector ↗
0.000 2.000 0.000 1.000
2.000 2.000 1.000 2.000
0.000 1.000 2.000 1.000
1.000 2.000 1.000 0.000
Check : (x,y,z)(0,1,0) vector ↑
2.000 1.000 2.000 1.000
1.000 4.000 1.000 1.000
2.000 1.000 2.000 1.000
1.000 1.000 1.000 2.000
Check : (x,y,z)(-1,1,0) vector ↖
0.000 2.000 1.000 1.000
2.000 2.000 2.000 1.000
1.000 2.000 0.000 1.000
1.000 1.000 1.000 0.000 0°方向ベクトルのGLCMを対称に、正規化後の確率分布を表示してみます。
System.out.println("Normalized distribution at 0 degree");
double[][] mat_norm = test.normalize(mat_0);
System.out.println(test.toString(mat_norm));//出力
Normalized distribution at 0 degree
0.000 0.125 0.000 0.083
0.125 0.083 0.125 0.083
0.000 0.125 0.083 0.000
0.083 0.083 0.000 0.000 特徴を計算する
RadiomicsJでは、各ベクトルで得られたGLCMについて、3D averagingによって特徴の集約を行います。以下、その結果を示します。
ImagePlus ds_pair[] = TestDataLoader.digital_phantom1();
ImagePlus imp = ds_pair[0];
ImagePlus mask = ds_pair[1];
RadiomicsJ.targetLabel = 1;
GLCMFeatures glcm = null;
try {
glcm = new GLCMFeatures(imp, mask, 1 ,1,true,6,null,null);
} catch (Exception e) {
e.printStackTrace();
}
System.out.println(GLCMFeatureType.JointMaximum+":"+glcm.calculate(GLCMFeatureType.JointMaximum.id()));//OK
System.out.println(GLCMFeatureType.JointAverage+":"+glcm.calculate(GLCMFeatureType.JointAverage.id()));//OK
System.out.println(GLCMFeatureType.JointVariance+":"+glcm.calculate(GLCMFeatureType.JointVariance.id()));//OK
System.out.println(GLCMFeatureType.JointEntropy+":"+glcm.calculate(GLCMFeatureType.JointEntropy.id()));//OK
System.out.println(GLCMFeatureType.DifferenceAverage+":"+glcm.calculate(GLCMFeatureType.DifferenceAverage.id()));//OK
System.out.println(GLCMFeatureType.DifferenceVariance+":"+glcm.calculate(GLCMFeatureType.DifferenceVariance.id()));//OK
System.out.println(GLCMFeatureType.DifferenceEntropy+":"+glcm.calculate(GLCMFeatureType.DifferenceEntropy.id()));//OK
System.out.println(GLCMFeatureType.SumAverage+":"+glcm.calculate(GLCMFeatureType.SumAverage.id()));//OK
System.out.println(GLCMFeatureType.SumVariance+":"+glcm.calculate(GLCMFeatureType.SumVariance.id()));//OK
System.out.println(GLCMFeatureType.SumEntropy+":"+glcm.calculate(GLCMFeatureType.SumEntropy.id()));//OK
System.out.println(GLCMFeatureType.AngularSecondMoment+":"+glcm.calculate(GLCMFeatureType.AngularSecondMoment.id()));//OK
System.out.println(GLCMFeatureType.Contrast+":"+glcm.calculate(GLCMFeatureType.Contrast.id()));//OK
System.out.println(GLCMFeatureType.Dissimilarity+":"+glcm.calculate(GLCMFeatureType.Dissimilarity.id()));//OK
System.out.println(GLCMFeatureType.InverseDifference+":"+glcm.calculate(GLCMFeatureType.InverseDifference.id()));//OK
System.out.println(GLCMFeatureType.NormalizedInverseDifference+":"+glcm.calculate(GLCMFeatureType.NormalizedInverseDifference.id()));//OK
System.out.println(GLCMFeatureType.InverseDifferenceMoment+":"+glcm.calculate(GLCMFeatureType.InverseDifferenceMoment.id()));//OK
System.out.println(GLCMFeatureType.NormalizedInverseDifferenceMoment+":"+glcm.calculate(GLCMFeatureType.NormalizedInverseDifferenceMoment.id()));//OK
System.out.println(GLCMFeatureType.InverseVariance+":"+glcm.calculate(GLCMFeatureType.InverseVariance.id()));//OK
System.out.println(GLCMFeatureType.Correlation+":"+glcm.calculate(GLCMFeatureType.Correlation.id()));//OK
System.out.println(GLCMFeatureType.Autocorrection+":"+glcm.calculate(GLCMFeatureType.Autocorrection.id()));//OK
System.out.println(GLCMFeatureType.ClusterTendency+":"+glcm.calculate(GLCMFeatureType.ClusterTendency.id()));//OK
System.out.println(GLCMFeatureType.ClusterShade+":"+glcm.calculate(GLCMFeatureType.ClusterShade.id()));//OK
System.out.println(GLCMFeatureType.ClusterProminence+":"+glcm.calculate(GLCMFeatureType.ClusterProminence.id()));//OK
System.out.println(GLCMFeatureType.InformationalMeasureOfCorrelation1+":"+glcm.calculate(GLCMFeatureType.InformationalMeasureOfCorrelation1.id()));//OK
System.out.println(GLCMFeatureType.InformationalMeasureOfCorrelation2+":"+glcm.calculate(GLCMFeatureType.InformationalMeasureOfCorrelation2.id()));//出力
JointMaximum:0.5028111707544143
JointAverage:2.142995006041697
JointVariance:3.0993207892076144
JointEntropy:2.3997112783734362
DifferenceAverage:1.4309811764537266
DifferenceVariance:3.056282621701805
DifferenceEntropy:1.5627332773445468
SumAverage:4.285990012083394
SumVariance:7.072803163045828
SumEntropy:1.9226064533586105
AngularSecondMoment:0.30297525027879985
Contrast:5.324479993784631
Dissimilarity:1.4309811764537268
InverseDifference:0.676615133317691
NormalizedInverseDifference:0.8506785598098696
InverseDifferenceMoment:0.6177393637968712
NormalizedInverseDifferenceMoment:0.8984432172242564
InverseVariance:0.06041630527029386
Correlation:0.15735003010076218
Autocorrection:5.055436010129556
ClusterTendency:7.072803163045828
ClusterShade:16.64409305005416
ClusterProminence:144.70338141184223
InformationalMeasureOfCorrelation1:-0.15684823480154977
InformationalMeasureOfCorrelation2:0.5195878631159618RadiomicsJの引用はこちら
Kobayashi, T. RadiomicsJ: a library to compute radiomic features. Radiol Phys Technol 15, 255–263 (2022). https://doi.org/10.1007/s12194-022-00664-4
RadiomicsJのリンク
https://github.com/tatsunidas/RadiomicsJ
Stay visionary
この記事が気に入ったらサポートをしてみませんか?
