
クリスマスプレゼントの箱のリボン (?)
この記事はペンシルパズルAII Advent Calendar 2019、25日目の記事です。
0. 序文
はじめまして、utimeです。アドカレの色々な記事、楽しく読ませていただきました。どれも素晴らしく、それらを色とりどりのクリスマスプレゼントに例えるなら、当記事はクリスマスプレゼントの箱のリボン (?)のようなものですが、楽しんでいただければ幸いです。
1. 自己紹介
改めまして、utimeと申します。東京大学ペンシルパズル同好会に所属してます。
自己紹介に興味がある......そのまま
自己紹介に興味がない......2. へ進む
基本的には解き手で、コンテストもちょくちょく参加してます。特にWPC、WSC予選やJPCへの出没率が高いです。
好きなパズルはP(パズル)全般なのですが、得意なのはS(数独)の方です。深い事情があってニコリ系パズルが苦手で、へやわけやましゅには苦労してます。
その他数オリをやってた時期もあったり、最近はオセロも嗜んでたりします。
自己紹介内容を厳選したら結構すっきりした。
2. ハイブリッド
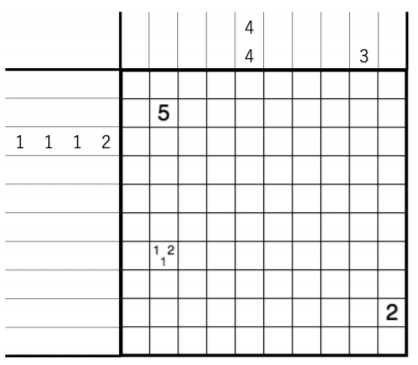
まずは次のシンプルループTapaトーラスロジックを解いて下さい。パズ同が東京大学の学祭で出した冊子の別紙「ハバネロ」に載せたものと同じです。
ルール
①盤面はトーラスです。すなわち盤面の上端は下端とつながり、左端は右端とつながっています。(「シームレス」という表記も多い)
②盤面のいくつかに黒マスが入ります。また、黒マス以外のマスを一度ずつ通るループ(シンプルループと同じ)が存在しますが、このループはトーラスが適用されます。
③黒マスはTapaの制約をみたします(盤面内部の数字はTapaのヒント数字です)。つまり連結かつ2×2禁(どの頂点も高々3つの黒マスにしか含まれない)で、これもトーラスが適用されます。
④盤面左、上のヒント数字はイラストロジックのヒント数字です。これに合うように黒マスをいれましょう。これもトーラスが適用されます。(つまるところ、5列目に4 4とあるので、5列目には黒マスを4つ挟んで2つの白マスが入る、といった感じ。)
penpa-editorはこちらから。またはこちら(URLが長いときのpenpa-editorの挙動が最近怪しいので。IEだとこっちでも開けないっぽい)。一応パズプレのTapaでのURLも貼っておく。
もちろん正誤判定は出ないけど、Tapaに線を引けるだけでもありがたい。
というわけで当記事は12月6日にょろっぴぃさんの神記事 ハイブリッドパズルについて の子記事となっております。
解けた方....................4. へ進む
解けなかった方......3. へ進む
3. 解説
解けなかった方、気を落とさないで下さい。今の所、観測できた限りではチェッカーのfffさん(アドカレの記事はこちら(AII))と、枝豆さんしか解けていません。
本質は「トーラス盤面にループと黒マス(連結)を置く」ということで、これを軸に考えます。
(そもそもトーラスとはドーナツ型のことで、長方形の紙の上端と下端をつなげて筒状にした後、左端と右端をつなげると、ドーナツ状になることが分かるかと思います。)
トーラス上のループを、Uターンしている箇所がなくなるように、交差させることなくなめらかに移動させると、例えば以下のようになります。

ここで、上辺を横切る線をn本、左辺を横切る線をm本とし、n、mの組としてありうるものを考えます。n、mが公約数dを持つときループがd本になることからn、mが互いに素であることが条件と分かります(n=m=0の場合は4 4の列に注目すると除外できる)。
ループをなめらかに移動させるのと同時に黒マスもなめらかに変形させると、ループがない箇所が黒マスとなり、帯状(輪っか)であることが分かります。

ここで並行するループが接してしまっている場合を考えます。(%)のように、ループのない箇所は帯状からただの塊に変わります。
さらにもう一度接してしまうと、今度は($)のように塊が2つに分断されてしまいます。

以上より「n、mは互いに素」「ループは多くても1度しか接しない」が条件と分かりましたが、ここでTapaのヒント1 1 2を考えると、以下のどちらの場合でもループが接してしまっていることが分かり、「1 1 2の箇所以外ループが接しない」ことが条件と分かりました。

あとは普通の激辛ハバネロレベルです。
4. 連結性
ところで、「ループが接する」には下図のような場合も含まれるわけですが、黒マスと黒マス以外が斜めに交差する配置が許されないパズル、見たことがあるのではないでしょうか。

はい、正解はしろまるくろまる(Yin-Yang)です。シンプルループTapaトーラスロジックはYin-Yangのバリエーションでした。ちゃんちゃん。
まとめると「ループ+連結」という大域条件が「接触禁」という局所条件に化けた訳ですが、この手の大域手筋も少し大事かと思ったのでまとめてみます。
というわけで当記事は12月2日SP1さんの神記事 大域手筋まとめ の子記事ともなっております(にしては内容が薄すぎるが(「双対盤面・内外」の節とも兼ね合う))。
4.0 概要
何かと何かを連結させたい、というのはどちらかといえば大域的な制約でありながら、直ちに局所的な条件が従うこともあります。
影響のある領域が広い分、偶奇と同じくらい仮定との相性が悪い(仮置きで解きにくい)かも。
4.1 数字埋め系
特になし。
4.2 線引き系
例えばスリザーリンクなどで、以下の上端と下端をつなぎたいと思うと以下の線が確定するのですが、多くの場合偶端理論で説明が付きます。

つなぐ対象が明示的に示されている場合、例えばナンバーリンクでは以下の線が確定します。

この迂回の考え方はナンバーリンクでは頻出で、他にも数字つなぎやリンク絵で出てきます(がこれくらいしか思いつかない)。大域的な考察ではあるもののヒント数字に強く依存しているため、大域手筋と呼ぶかどうかは不明です。
4.3 塗る系
Tapaなどでも4.2と同様に、黒マス同士を連結させるために黒マスになる必要があるマスが決定することがあります。
しろまるくろまるのオセロ配置禁はよく知られている通りです。連結性の花形ですが、黒マスも黒マスの補空間も連結であるパズルは上述のような特殊例を除き無い(と思う)ので汎用性は低いです。
4.4 配置系
特になし。
4.5 分割系
特になし。
大域手筋まとめ の方には汎用性の高い大域手筋が多数収録されているので必見です。
5. 最後に
5.1
シンプルループTapaトーラスロジックのヤバさの所以は、仮定との相性が悪い手筋があり、これが盤面のいたるところに現れるため、二重、三重程度の仮定では解き進められないことだと思います。今後、表出に依存しない制約が盤面の全域に現れるパズルはもう出てこないとは思いますが、いざという時のために、初見パズルの解析はした方が良いかもしれません。軽い制約くらいは見つかることもあるかも。
5.2
クリスマスはどのようなご予定でしょうか?特に予定がない方のために、こんなパズルを用意しました。
シンプルループTapa (?)
①黒マス、ヒント数字はTapaに準じる。
②ループは黒マス以外を1度ずつ通る。

リンクはこちらまたはこちら。解けたらこちらに、ABCDの列に入った黒マス数(二桁の場合下一桁)を並べた半角数字4ケタを入力して下さい。ツイート出来る場合は是非ツイートして下さい。ふぁぼりに行きます。
最後になりますが、メリークリスマス。そしてよい年越しを。ついでにあけましておめでとうございます。
