
太いワ細いサ 偶奇のワルツ
"舞踊"ろうぜ・・・"偶奇"の"円舞曲"をよ・・・
0. 概要
「太いワ細いサ」は、ニコリ174号初出のオモパです。
明らかに強い制限、2種の線からなる奇抜な見た目・・・といった特徴があり非常に好きなパズルだったのですが、制限の強いパズルの宿命か、次号での掲載はありませんでした。
特に、その制約の強さから大域的な偶奇性が存在し、それを利用して作った問題がこちらです(数か月前にTwitterに流したやつです)↓

問題のURLはこちら
(細線は「辺>>通常>>緑」、太線は「辺>>通常>>二重」で正解判定)
(ちなみに解説を見れば分かりますが、表出の線の太さを不明にしても唯一解になります)
これで唯一解になるという事実が制約の強さを物語っていますね。
ですが安心してください。太いワ細いサの偶奇性を理解すれば、ちゃんと理詰め(1手先読みぐらい)で解けるようになっています。
という訳で、この記事では
①太いワ細いサの偶奇性
②上の問題の解き方
の解説を行いたいと思います。
また、1つ注意事項として、ニコリ本誌では盤面に点線の罫線がついていた記憶がありますが、penpa-editorとの相性や見やすさから、スリザーリンクのように格子点だけの盤面にしています。
1. ルール
①点と点の間に太線か細線のいずれかを引き、全体で1つの輪っかを作りましょう。
②線を交差させたり、枝分かれさせてはいけません。
③既に引いてある線はループの一部になり、その両端で曲がります。
④ループの各直線部分は太線か細線のいずれかになります。
太線の長さは、その辺と隣接する2辺の長さの和になります。
細線の長さは、その辺と隣接する2辺の長さの差になります。
例題

例題のURLはこちら
(解答画像と違い、太線を辺>>通常>>二重、細線を辺>>通常>>緑で入力すると正解判定が出ます。)
解答

今手元にニコリ本誌が無いので確認できませんが、確かこんなルールだったと思います。本来は点線の上に線を引くパズルなので、①は本誌では書きぶりが違うはずです。
また、断腸の思いですが、話の見通しをよくするためにこの記事内では線の太さを全部一緒で表すことにします。
2種類の線という太いワ細いサのチャームポイントが失われるのは大変心苦しいですが、その方が簡潔なのでそうします。
2. 最大公約数
長さAマスの辺とBマスの辺が隣合っているとします(A≧Bとする)。
このとき、ルールからその2辺に隣り合う辺の長さは、
・A+Bマス
・A−Bマス (A>Bの場合に限る)
のいずれかになります。
ここで、AとBの最大公約数について考えると、
gcd (A, B) = gcd (A, A±B)
が成り立つことが知られています。但し、
gcd (A, B) = (AとBの最大公約数)
とします。(gcd は greatest common divisor の頭文字です)
このへんは数ⅠAだかのユークリッド互除法でやるんじゃないでしょうか。
このことから、太いワ細いサの解答となるようなループ(太細ループと呼ぶことにします)は次の条件を満たすことが分かります。
太細ループの隣り合う2辺の長さの最大公約数は、ループ内で常に一定
特に、太細ループの中で偶数長の2辺が隣合った時点で、全辺の長さが偶数になります。
上の性質から、太細ループを調べる上では、任意の隣接2辺の長さが互いに素なものを考えれば十分であるといえます(もしそうでなければ、ループ全体を最大公約数分の1倍に縮小すればよい)。
そのため、次章では隣あう2辺の長さは互いに素、と仮定して話を進めます。
3. ぐうきっき
直前で強調したように、ここでは隣り合う2辺の長さが互いに素な太細ループの性質を調べます。
【辺の長さの偶奇】
前提条件から偶数長の辺同士は隣合わないので、当然ループのどっかに奇数長の辺が存在します。
そうすると、その両隣の2辺の和か差が奇数になるので、両隣の2辺の一方は偶数、もう一方は奇数になります。
この議論を続けることで、ループ内の辺の長さは
偶、奇、奇、偶、奇、奇、偶、奇、奇、偶、・・・
と周期3の繰り返しになることが分かります。
ところで、この「偶、奇、奇、偶、奇、奇、」というリズム、どこかで聞き覚えがあるような・・・?
そうです!これはワルツの「ズンチャッチャ、ズンチャッチャ」というリズムと一緒ですね!
せっかくなので、この繰り返しを偶奇ワルツと呼ぶことにしましょう。
更に、辺の縦横も考えると、
偶ー、奇|、奇ー、偶|、奇ー、奇|、偶ー、奇|、奇ー、・・・
と周期6の繰り返しになることが分かります。6拍子ですね。
このことから、太細ループは必ず6の倍数本の辺からなることがが分かります。
【辺の配置の偶奇】
上記の長さ・縦横に関するパリティが、実際の盤面でどのように振る舞うのか見てましょう。
まず、盤面の格子点を図のように市松模様に塗ります。

すると、
・偶数長の辺の両端は同じ色
・奇数長の辺の両端は異なる色
になります。
2回続けて奇数移動すると元の色に戻るので、前述の偶奇ワルツ性から次が従います。
盤面の格子点を市松模様に塗り分けたとき、
太細ループ内にある全ての偶数長辺の端点は、同じ色の格子点上にある。
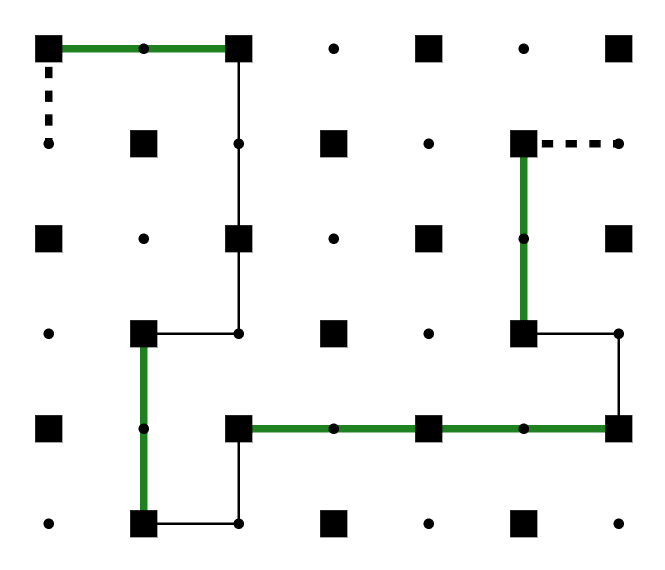
上の図のように、偶数長辺(緑線)の両端が全て黒四角■の上に乗ることが分かります。
ここで、偶数長辺の端点があり得る格子点を、図のようにさらに市松模様に色付けします。

このとき、縦奇数マス+横奇数マスの動きによって、必ずもう一方の色の格子点へ移ることが分かります。

したがって、線の縦横も考慮した周期6の偶奇ワルツ性から、次が従います。
上の格子点塗り分けにおいて、
太細ループ内にある全ての縦偶数長辺の端点は同じ色の格子点上に、
横偶数長辺の端点はもう一方の色の格子点上にある。
これまでの結果をまとめるとこんな感じになります。

太細ループの偶奇ワルツ性
縦の偶数辺は灰四角■、横の偶数辺は白四角□に乗っていることが分かります。
さっきまでごちゃごちゃ書きましたが、とりあえずこの図を見ておけばどうにかなります。
このように、かなり強い大域制約が見つかりました。
これを使えば、例えば下のような適当に辺を2つ配置した問題が既に破綻していることが分かります。

解なし
太いワ細いサを作る時はこの制約に気を付けましょう。
逆に表出がこの条件さえ満たしていれば、あとはわちゃわちゃやれば大体うまいこと引っ付くと思います。
安心してどんどん太いワ細いサを作りましょう!!
4. 2辺表出問題の解説
という訳で、冒頭で挙げた例の問題の解説に移ります。

まずは見るからに偶奇を使ってほしそうな長さ2の表出があるので、格子点を塗ってその偶奇性を暴いてやりましょう。

・・・なんか同じ色の格子点に縦線と横線が乗ってません?

パズスクで来たらビビるやつですね。
さっきまでの解説は全部夢だったのでしょうか。
当然そんなことはありません。
定理が当てはまらない場合は、まず前提条件が満たされているか確認しましょう。
・・・
そこでよくよく考えると、先ほどの議論は
「隣り合う2辺の長さは互いに素」
という前提を置いていました。
つまり、その前提下で破綻するということは、この問題の解となるループは隣り合う2辺の長さが常に2以上の最大公約数を持つことが分かります。
さらに、長さ2の辺が既にあるので、ループの辺の長さは全て偶数になります。
従って、この問題は全体を1/2倍することにより、次の問題と同じとみなせます。

ここまで縮むとなんかいけそうですよね。
あとは順を追って地道に解いていきましょう。
再度注意ですが、この記事では簡単のため太線と細線を区別せず書いています。

まず、表出辺の両端では必ず曲がるので、直ちにここまで進みます。
ここで、A=1(辺Aの長さが1)だとすると、そこから上に2マス伸びないといけないので破綻します。また、A=3だとしても右の辺とひっついて破綻するので、A=2で確定します。
同様に、B=1だと破綻するので、B≧2と分かります。
それらのことから、下図ぐらいまで自然に進みます。

ここで、辺Aは偶数長なので、偶奇ワルツ性から辺Cは偶数長、辺Bは奇数長と分かります。
特に、C=2か4のいずれかになります。
ここで、C=4も入らんやろ~と思いながらC=4と仮定します。

すると、辺Cの下端で3マス以上横に伸びないといけませんが、そんなスペースは無いので案の定破綻します。
よって、C=2です。
ここまでくれば、あとは流れで行けます。

最後が若干確定しないですが、上図の1マスの隙間でループが閉じないと破綻することがなんやかんやで分かるので、閉じます。

出来上がりです。あとはこれを2倍すれば、元の問題の答えになります。

答えです。お疲れ様でした。

せっかくなので、本来太線になる部分を二重線にしました。
やっぱり線が2種類あるのは面白いですね。
5. 制約の強いパズルはいいぞ
いかがでしたか?
私自身、最初に太いワ細いサを作った時やけに破綻したので、なんだこれはと見てたらこんなものが隠されていました。
制約の強い、"固い"パズルを作っていると割とこういうことがあります。以前にも、メジリンクを作っているときに「ループの内側の面積は偶数マスになる」ことに気づかず、えらい目にあった経験があります。
そうした事態に直面した時、「やっぱ制約強いパズルしんどやめよ」となるか、「何か原因があるのでは調べよ」となるかで得られるものが変わってくると思います。手間がかかるかもしれませんが、覗き込んでみると新しい発見があるかもしれません。
何はともあれ太いワ細いサを作ろう!!!!!!!
この記事が気に入ったらサポートをしてみませんか?
