相似比と線分比

中学３年で相似を習ったときに、相似比をどのように教わったでしょうか。
また、どのように覚えているでしょうか。
相似比の教え方・覚え方としては、

• 相似比は線分比と同じ

• 相似比は簡単に言うと線分比

の、どちらかが多いのではないかと思います。
私が教えるときは、
相似比は線分比から求められ、結果としては相似比と線分比は同じになる
等のように、相似比と線分比は同じではないという印象を与えるように教えます。
これは、相似の後半で習う内容で間違わないようにするためです。

今回は、まず相似・相似比とは何かについて書きます。
この後、相似比から面積比の求め方について書きます。
最後に、面積比に関する似た問題として、平行線と面積比について書きます。
このときに、なぜ相似比と線分比は同じではないという印象を持たせるかについて書きます。

相似・相似比

相似とは拡大・縮小に関することです。
図を、

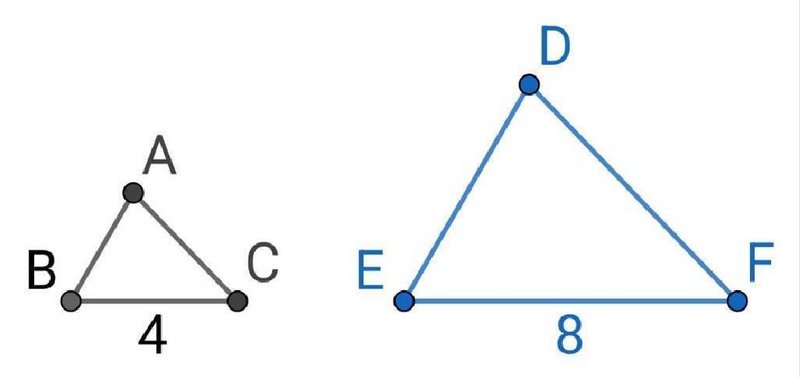
のような、２つの相似な三角形について考えてみましょう。
この図では、左の三角形を２倍拡大すると右の三角形と合同になります。
このように、２つの図形のうち片方を拡大または縮小すると、もう片方の図形と合同になるとき、これら２つの図形は相似と言います。

また、相似比とは２つの図形の比のことです。
つまり、

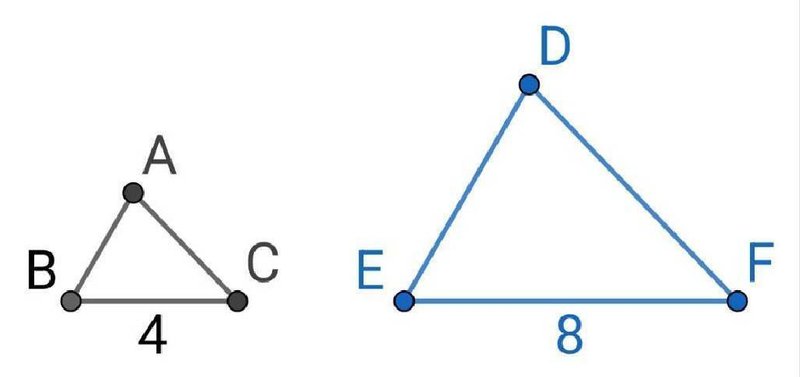
のような２つの相似な三角形の場合は、左の三角形を２倍拡大すると右の三角形と合同になるので、相似比は$${ 1:2}$$となります。
相似比の求め方としては、対応する辺の長さから、
$${4:8=1:2}$$
と計算できます。

相似比と面積比

相似比が$${ a:b}$$のとき面積比は、
$${ a^2:b^2}$$
となります。
図を、

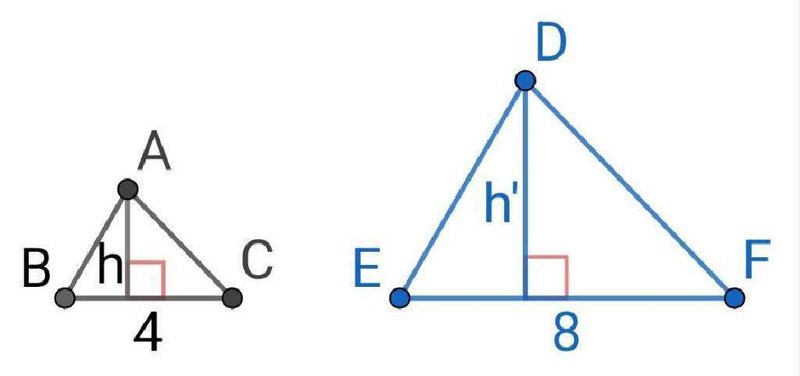
のような、２つの相似な三角形の面積について考えてみましょう。
相似比は、
$${4:8=1:2}$$
となります。
このとき、長さに関しては相似比と同じになるので高さは、
$${ h:h'=1:2}$$
より、
$${ h'=2h}$$
となります。
この$${ h:h'=1:2}$$となることは、最後に補足で証明します。
$${ \triangle ABC}$$の面積は、
$${ \triangle ABC=\dfrac{1}{2} \times 4 \times h=2h}$$
となります。
$${ \triangle DEF}$$の面積は、
$${\triangle DEF=\dfrac{1}{2} \times 8 \times h' }$$
となり$${ h'=2h}$$より、
$${\dfrac{1}{2} \times 8 \times h'=\dfrac{1}{2} \times 8 \times 2h=4 \times 2h }$$
となり$${ 2h =\triangle ABC}$$より、
$${4 \times 2h=4 \times \triangle ABC}$$
となるので、
$${\triangle DEF=4 \times \triangle ABC=2^2 \times \triangle ABC}$$
となります。
よって、
$${\triangle ABC : \triangle DEF=1^2:2^2}$$
となります。
また、このことは簡単には、底辺と高さの２つの長さが相似比である$${1:2}$$となることから、
$${\triangle ABC : \triangle DEF=1^2:2^2}$$
と面積比が求められると考えることもできます。

平行線と面積比

図を、

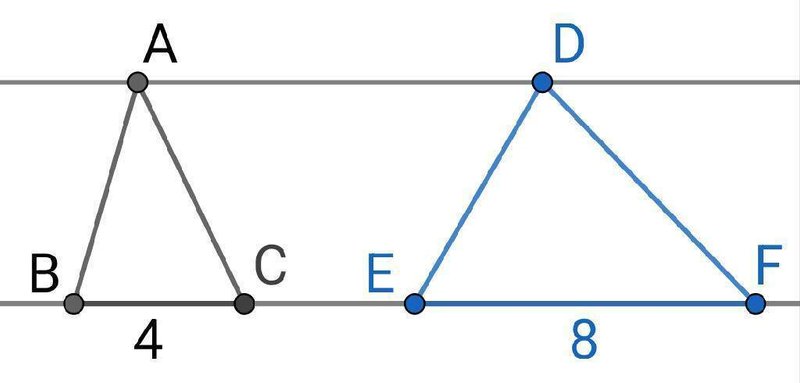
のようにし、$${ AD//BF}$$とします。
では問題です。
$${\triangle ABC,\triangle DEF}$$の面積比は、どのようになるでしょう。

$${ BC:EF=4:8=1:2}$$
となるから、
$${\triangle ABC:\triangle DEF=1^2:2^2=1:4}$$

というのは、間違いです。
このような間違いをしないために、私が教えるとき、

相似比と線分比は同じではない

という印象を与えるように教えます。
では、なぜ$${\triangle ABC:\triangle DEF=1^2:2^2}$$とは、ならないのか。
これは、相似比を使って計算しています。
改めて、

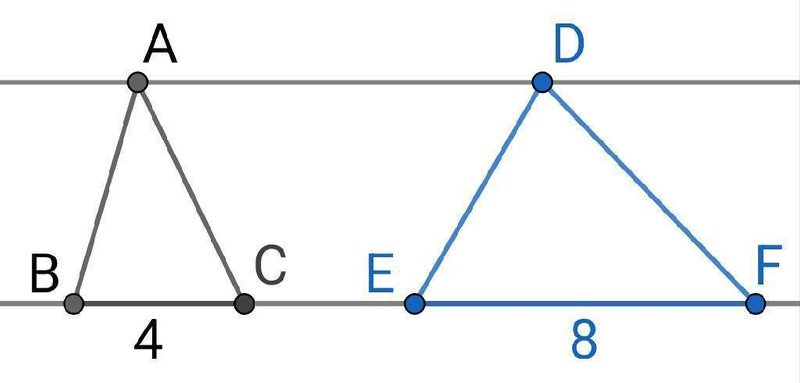
の図を見てみましょう。
この図からわかるように、$${\triangle ABC,\triangle DEF}$$は相似ではありません。
相似比を使って面積比を求めようとしても、相似比が存在しません。
では、どのようにして面積比を求めるのか。
これは、中学２年で学んだ内容を使います。
２つの三角形の高さは、２本の平行線の距離となり、同じ長さです。
２つの三角形で違うのは、底辺だけとなります。
このことにより、面積比は底辺の比と同じになるので、
$${\triangle ABC:\triangle DEF=4:8=1:2}$$
となります。

ここで書いた、
$${\triangle ABC:\triangle DEF=1^2:2^2}$$
と間違える理由の１つに、相似比と線分比が同じものと考え、相似比という単語自体を忘れていたり、意識していないことがあると思います。
これは、相似比が線分比から簡単に求められることがあると思います。
これらにより相似比という単語を聞いても、頭の中で相似比がすぐに線分比と変換されている場合もあると思います。
しかし、相似比と線分比は同じではないという印象があり、相似比という単語をわかっていれば、
$${\triangle ABC:\triangle DEF=1^2:2^2}$$
と間違ったとしても、$${\triangle ABC,\triangle DEF}$$は、

相似ではない

の一言で理解できると思います。

まとめ

今回は、相似比と線分比は同じではないという印象を与えるように教える理由について書きました。
このようにしておくと、平行線と面積比で扱ったような問題で間違いにくくなるでしょう。
特に数学が苦手だと、相似比と線分比が同じという印象があるかもしれません。
相似比という単語が出てきたとき、頭の中ではすぐに線分比のことと変換されているかもしれません。
しかし、最初から相似比と線分比は同じではないという印象があれば、間違う可能性が低くなり、もし間違えてもすぐに修正できると思います。
また教える場合は、相似比と面積比を教えた直後に、平行線と面積比で扱ったような問題を復習したほうが良いと思います。

補足

図を、

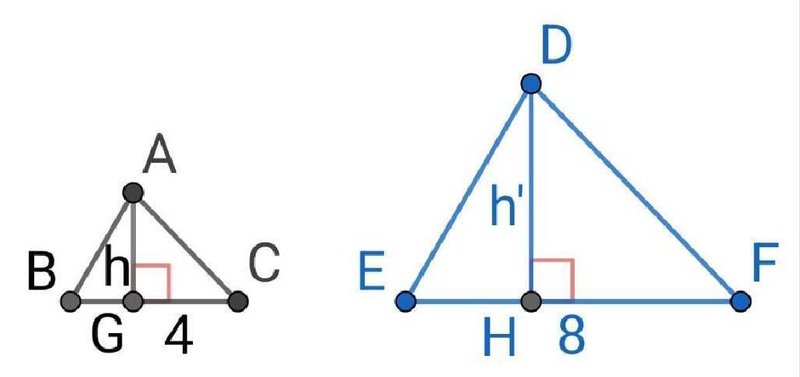
のように、$${\triangle ABC,\triangle DEF}$$は相似な三角形、$${ BC=4,EF=8}$$とします。
また、$${\triangle ABC}$$の高さを$${ AG}$$、$${\triangle DEF}$$の高さを$${ DH}$$、$${AG=h,DH=h'}$$とします。
このとき、$${ h:h'=1:2}$$となることを証明します。

証明

$${\triangle ABC,\triangle DEF}$$は相似なので、
$${ \angle ABG=\angle DEH}$$
$${AG,DH}$$は高さなので、
$${ \angle AGB=\angle DHE=90 \degree}$$
$${ \angle ABG=\angle DEH,\angle AGB=\angle DHE}$$より、
二組の角が等しいので、
$${\triangle ABG,\triangle DEH}$$は相似となる
また$${ BC=4,EF=8}$$より、$${\triangle ABC,\triangle DEF}$$の相似比は、
$${BC:EF=4:8=1:2}$$
となるので、
$${AB:DE=1:2}$$
$${\triangle ABG,\triangle DEH}$$は相似、$${AB:DE=1:2}$$より、
$${\triangle ABG,\triangle DEH}$$の相似比は、
$${AB:DE=1:2}$$
となり、
$${AG:DH=h:h'=1:2}$$