【超速まとめ】 一次関数（一次関数の式・変化の割合・グラフ・二元一次方程式）

「一次関数」の章を一目で理解できるように、重要事項を最も簡単にまとめました。

１、一次関数とは何か

(1)yがxの関数で、yがxの一次式で表わされるものを一次関数という

最初にいくらかの量があり、それから決まった割合で増えていく2つの量があるとき、2つの量の関係が一次関数である

（例）水が5L入っている水そうに毎分2Lの割合で水を入れるとき、水を入れ始めてからx分後の水そう中の水の量をyLとする
最初の量が5で、毎分2ずつ増え続けるから、y=2x+5

(2)すべての一次関数は、y=ax+bの式で表すことができる
最初の量がbで、aずつ変化することを表している

(3)比例y=axは、最初の量bが0の一次関数である
反比例y=a/xは、一次関数ではない
2乗に比例y=ax2は、xの2次式だから一次関数ではない（2次関数という）

２、xの増加量、yの増加量、変化の割合

「xの増加量」、「yの増加量」、「変化の割合」の問題は、それぞれを求める公式を正確に覚えないといけない

例題１：一次関数y=3x+1について、次の問いに答えよ。

(1)xの値が2から5まで増加するときのxの増加量を求めよ。
xの「増加量」とは、xが「いくら増えたか」ということだから、xの最初の量x1を、xの後の量x2からひく
xの増加量は、2から5になったので5-2=3

xの増加量を求める式は、x2-x1

(2)xの値が2から5まで増加するときのyの増加量を求めよ。
yの「増加量」とは、yが「いくら増えたか」ということ
x=2のときのyの値と、xが5のときのyの値を、y=3x+1の式にx=2とy=5を代入してyの値を求めてから、yの最初の量y1を、yの後の量y2からひく
x=2のとき、y=3×2+1=7
x=5のとき、y=3×5+1=16
yの増加量は、7から16になったので16-7=9

yの増加量を求める式は、y2-y1

(3)xの値が2から5まで増加するときの変化の割合を求めよ。
「変化の割合」とは、「xが1増えるごとにyはいくら増えるか」ということ
変化の割合は、xが3増えるとyは9増えたので、9÷3=9/3=3

変化の割合を求める式は、変化の割合=yの増加量/xの増加量=y2-y1/x2-x1

ところが、一次関数y=ax+bでは、変化の割合は常にaになる
変化の割合=a

(4)xの増加量が4のときのyの増加量を求めよ。
「xの値が4のときのyの値を求めよ」という問題ならば、式y=3x+1にx=4を代入してy=13だが、「xの増加量が4のとき」だから、代入ではない

「増加量」とあるときは、「変化の割合」つまりy=ax+bのaだけに関する問題である

「変化の割合」=「xが1増えるごとにyはa増える」という意味だから、xが4増えるとyはa×4、つまり、この問題だと、3×4=12増える

３、一次関数のグラフ

一次関数のグラフを、傾きと切片を使ってかく

例題２：次の一次関数の傾きと切片をいい、それぞれのグラフをかけ。
(1)y=2x+1
(2)y=1/2x-3
(3)y=-3x+7

一次関数y=ax+bで、aを傾き、bを切片という
一次関数のグラフをかくときは、まず、y軸上に切片をとって、そこから右に傾きの分だけ進む

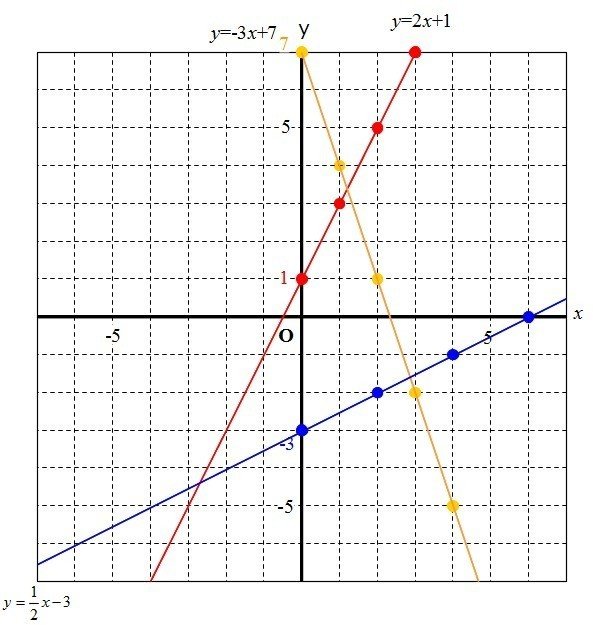
(1)y=2x+1
傾きは2、切片は1
y軸上に切片の1をとり、そこから右に、傾き2ずつ（右に1進むたびに上に2）進む

(2)y=1/2x-3
傾きは1/2、切片は-3
y軸上に切片の-3をとり、そこから右に、傾き1/2ずつ（傾きが分数のとき、右に2進むたびに上に1）進む

(3)y=-3x+7
傾きは-3、切片は7
y軸上に切片の7をとり、そこから右に、傾き-3ずつ（傾きが負の数のとき、右に1進むたびに下に3）進む

（注）例えば、一次関数y=2x+3のグラフは、比例y=2xのグラフを、y軸の正の方向に3だけ、平行移動したグラフである（y=2x-3なら、y軸の正の方向に-3、または、y軸の負の方向に3、平行移動したもの）

４、一次関数の式を求める

一次関数の式を求める問題には、次の6つの種類がある

例題３：次のような条件が与えられているとき、一次関数の式を求めよ。
(1)グラフを見て、直線の式を求めよ。
(2)点(-1,2)を通り、傾きが4の直線の式を求めよ。
(3)(-3,2)を通り、切片が3の直線の式を求めよ。
(4)点(1,-3)を通り、直線y=-4x-3に平行な直線の式を求めよ。
(5)2点(3,1)、(-2,-1)を通る直線の式を求めよ。
(6)x=3のときy=1で、xの増加量が2のとき、yの増加量が6である一次関数の式を求めよ。

一次関数の式を求める問題は、y=ax+bのaとbを見つけたらよい。

どの問題も、次の4段階で解くことができる。
1、y=ax+bで、aとbを見つけようと決める。
2、傾き（=変化の割合）=aの値を先に求める。
3、もう一つの条件から、bの値を求める。
4、y=ax+bの式のa,bに求めた数値を入れる・・・それが答え。

(1)グラフを見て、直線の式を求めよ。

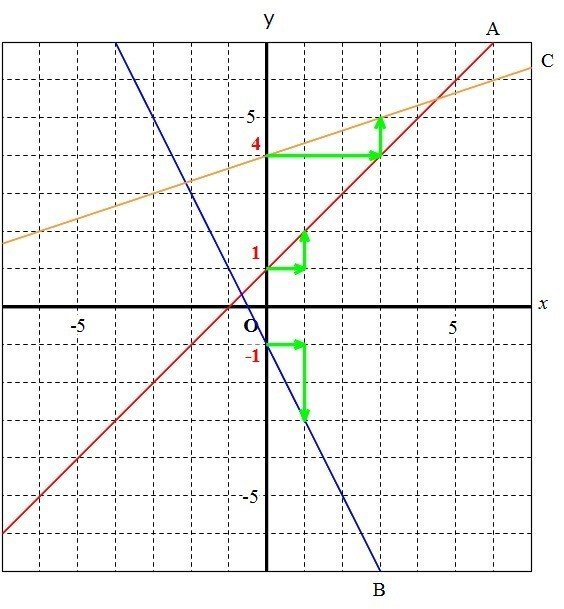
A…
1、y=ax+bで、
2、右へ1、上に1進んでいるから、傾きa=1
3、切片bは1
4、直線の式はy=x+1

B…
1、y=ax+bで、
2、右へ1、下に2進んでいるから、傾きa=-2
3、切片bは-1
4、直線の式はy=-2x-1

C…
1、y=ax+bで、
2、右へ3、上に1進んでいるから、傾きa=1/3
3、切片bは4
4、直線の式はy=1/3x+4

(2)点(-1,2)を通り、傾きが4の直線の式を求めよ。
1、y=ax+bで、
2、傾きが4だから、a=4
3、y=ax+bで、a=4だから、y=4x+b
この式が、
(-1,2)を通るから、x=-1、y=2を代入して、2=4×(-1)+b
この方程式を解いて、b=6
4、直線の式は、y=4x+6

(3)(-3,2)を通り、切片が3の直線の式を求めよ。
bを先に求めることが他の問題と違う
1、y=ax+bで、
2、切片が3だから、b=3
3、y=ax+bで、b=3だから、y=ax+3
この式が、
(-3,2)を通るから、x=-3、y=2を代入して、2=a×(-3)+3
この方程式を解いて、a=1/3
4、直線の式は、y=1/3x+3

(4)点(1,-3)を通り、直線y=-4x-3に平行な直線の式を求めよ。
平行なグラフは傾きaが等しい
1、y=ax+bで、
2、y=-4x-3に平行だから、傾きa=-4
3、y=ax+bで、a=-4だから、y=-4x+b
この式が、
(1,-3)を通るから、x=1、y=-3を代入して、-3=-4×1+b
この方程式を解いて、b=1
4、直線の式は、y=-4x+1

(5)2点(3,1)、(-2,-1)を通る直線の式を求めよ。
1、y=ax+bで、
2、まず、
傾き=変化の割合を求める式、

変化の割合=yの増加量/xの増加量=y2-y1/x2-x1を使って、aを求める

変化の割合（=傾き）=yの増加量/xの増加量=-1-1/-2-3=-2/-5=2/5
傾きa=2/5
3、y=ax+bで、a=2/5だから、y=2/5x+b
この式が、
(3,1)を通るから、x=3、y=1を代入して、1=2/5×3+b
この方程式を解いて、b=-1/5
4、直線の式は、y=2/5x-1/5

(6)x=3のときy=1で、xの増加量が2のとき、yの増加量が6である一次関数の式を求めよ。
1、y=ax+bで、
2、まず、
傾き=変化の割合を求める式
変化の割合=yの増加量/xの増加量を使って、aを求める
変化の割合（=傾き）=yの増加量/xの増加量=6/2=3
傾きa=3
3、y=ax+bで、a=3だから、y=3x+b
この式で、
x=3のとき、y=1だから、x=3、y=1を代入して、1=3×3+b
この方程式を解いて、b=-8
4、直線の式は、y=3x-8

以上のように、一次関数の式を求める問題は、どの問題も、次の4段階で解くことができる。
1、y=ax+bで、aとbを見つけようと決める。
2、傾き（=変化の割合）=aの値を先に求める。
3、もう一つの条件から、bの値を求める。
4、y=ax+bの式のa,bに求めた数値を入れて式を完成する

５、二元一次方程式とグラフ、連立方程式とグラフ

中1で学んだ一次方程式や、中2で学ぶ二元一次方程式は、グラフでは直線になる

例題４：次の方程式のグラフをかけ。
(1)-4x-2y-6=0
(2)10x+5y+20=0
(3)4x+20=0
(4)9x-12=6

一次関数y=ax+bの形に変形すれば、グラフをかくことができる

(1)-4x-2y-6=0
等式を変形する
-4x-2y-6=0
-2y=4x+6…両辺を-2でわる
y=-2x-3

(2)10x+5y+20=0
等式を変形する
10x+5y+20=0
5y=-10x-20
y=-2x-4

（別解）x軸との交点（y=0の点）、y軸との交点（x=0の点）の2点の座標がわかれば、グラフをかくことができる
10x+5y+20=0の式にy=0を代入してx軸との交点を求めると、
10x+20=0
10x=-20
x=-2
x軸との交点は、(-2,0)
10x+5y+20=0の式にx=0を代入してy軸との交点を求めると、
5y+20=0
5y=-20
y=-4
x軸との交点は、(0,-4)
2点(-2,0)、(0,-4)を通る直線をかけばよい

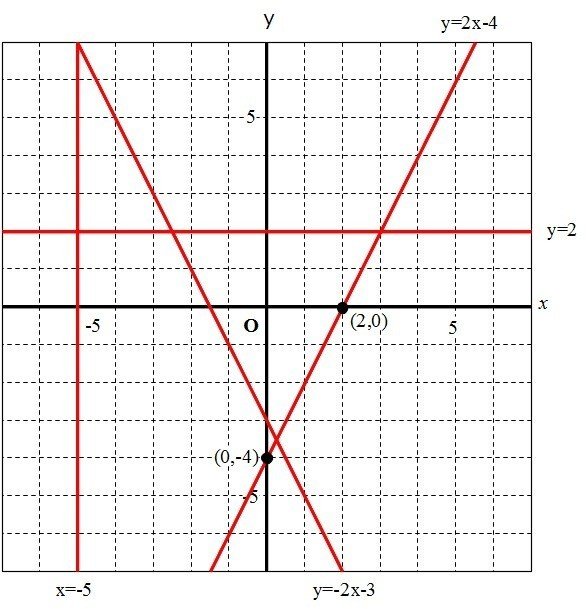
(3)4x+20=0
式を変形して、x=kの形にする
4x+20=0
4x=-20
x=-5

x=kのグラフは、y軸に平行な直線である

(4)9y-12=6
式を変形して、y=kの形にする
9y-12=6
9y=18
y=2

y=kのグラフは、x軸に平行な直線である

６、連立方程式とグラフ

連立方程式の解とグラフの交点の座標とは同じものである

例題５：
(1)次の連立方程式の解を、グラフを使って求めよ。
x-2y=6
2x+y=2

連立方程式の解とは、2つの式、x-2y=6と2x+y=2の両方の式が成り立つx,yの値である
グラフの交点の座標は、2つのグラフ、x-2y=6と2x+y=2の両方の式が成り立つx,yの値である
よって、連立方程式の解を知りたければ、グラフの交点の座標を読み取ればよい
連立方程式の解=交点の座標

y=ax+bの形に変形してグラフをかき、交点の座標を読み取る

x-2y=6より、
-2y=-x+6
y=1/2x-3

2x+y=2より、
y=-2x+2

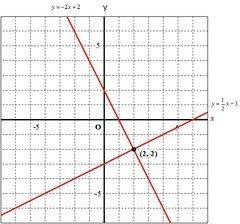
交点の座標が(2,-2)だから、連立方程式の解は、x=2,y=-2

(2)次の2直線の交点の座標を求めよ。
x+4y=-2
2x+3y=1

逆に、グラフの交点の座標を知りたければ、連立方程式を解いて解を求めれば、それが交点のx座標、y座標である
交点の座標=連立方程式の解

連立方程式を計算で解く

x+4y=-2…(1)
2x+3y=1…(2)

(1)×2-(2)
2x+8y=-4
2x+3y=1

5y=-5
y=-1

(1)に代入して、
x+4×(-1)=-2
x=2

連立方程式の解がx=2,y=-1だから、交点の座標は(2,-1)