数学嫌いなエンジニアでも使えるFFT処理の実用例
信号処理では「FFT」と言う技術が色々なところで使われています。プログラム言語ではライブラリーとしてFFTが準備されていますし、エクセルですらFFTがサポートされています。
FFTを使ってみようとFFT入門書などを探してみても、FFTの基本原理や基本的な使い方がほとんどで、「どんなことに具体的に使える」「どんな分析ができる」などがあまり書かれていません。
基本的な説明がどうしても数学がメインになってしまい、なかなか先へ進めません。そこで、数学的な考え方を余り使わないでFFTを使うことだけに絞った説明を書いてみたいと思います。
ここでは数学的な表現を少しは使いますが、基本、理解しないでも、使い方(手順)だけ覚えれば取りあえずFFT処理の結果を出すことに注力します。
■フーリエ(Fourier)、名前の由来
すでに固有名詞化していてあまり知られていませんが、フランスの数学者&物理学者のジャン・バティスト・ジョゼフ・フーリエ男爵(Jean Baptiste Joseph Fourier)から来ています。
フーリエと言う名前が付く固有名詞には「フーリエ級数」「フーリエ積分」「フーリエ変換」などいろいろありますがみんな親戚のような関係で、一番有名なのがフーリエ変換ではないでしょうか。簡単に言うと時間信号を周波数領域に変換するアルゴリズムです。
フーリエ変換の基本変換はDFT(Discrete Fourier Transformation)と呼ばれていますが、その中でも特に高速で変換できるアルゴリズムがFFT(Fast Fourier Transformation)と呼ばれるようになりました。
■FFTの入力信号と出力の関係
FFTは数学的表現だと「時間信号を周波数領域で複素数出力にする変換アルゴリズム」。簡単に言うと、1入力の時間信号を2出力の周波数成分に変換するアルゴリズムです。
FFTするための基本的な条件は2のn乗になるデータ列が必須です。下の例では32個のデータで計算しています。出力は32個の周波数成分になります。
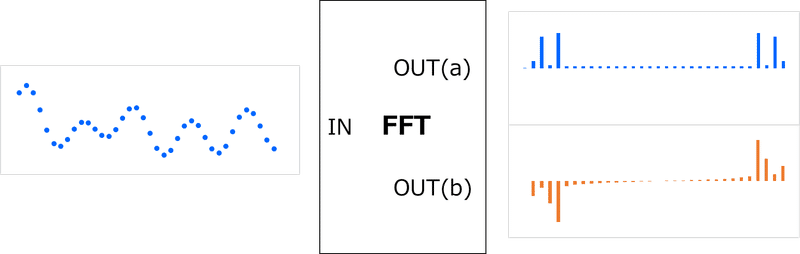
なぜ、2出力かと言うと周波数成分は「振幅」「位相」情報から成り立っているからです。FFT出力自体は「振幅」「位相」にはなっていませんが、この出力から計算で求められます。
信号sをFFTすると[a,b]が出力されますが、一般的にはa+biと複素数の型で出力されます。複素数と言ってもデータがそれぞれ独立していることを意味しているだけです。このデータから振幅と位相を求めてみると

■エクセルでFFT分析を試してみる
FFTをプログラムを書かないで簡単に試すにはエクセルが最適です。
最初に分析データを[D1:D32]に入力し、以下のような手順でフーリエ解析を行います。出てこない場合は[ファイル]→[オプション]→[アドイン]→[分析ツール]のチェックを最初に行ってください。

出力を[E1:E32]に設定すると複素数で計算結果が出てきます。

この結果から振幅や位相を求めるにはエクセル関数のIMABS( )、IMARGUMENT( )で簡単に求められます。
■FFTをハードウェアとしてイメージする
電気測定器ではスペクトラムアナライザー、オーディオ機器ではグラフィックイコライザーに相当します。要はバンドパスフィルタ(BPF)の集合体で、入力信号をそれぞれのBPFを通過させて周波数成分を分離します。

FFTのBPF毎の帯域幅の形は一般のBPFと違って理想的な形をしています。また、BPFの帯域幅はすべての周波数で同じになります。
■FFTの扱える最高周波数は何で決まる?
処理できる最高周波数はサンプリング周波数の半分の周波数になります。これはサンプリング定理をイメージしてもらえば良いと思います。サンプリング定理だとfs/2を中心に「0~fs/2」「fs/2~fs」成分は線対象になります。
しかし、最初の例で計算した32個FFTのb出力は対象になっていません。そこで出力の振幅を計算してみると

見事に中心周波数fs/2で左右対称(線対称)になりました。この図からわかるようにFFT分析では出力周波数は0~fs/2まであれば十分で、残りの周波数は必要ありません。この例では32個の入力データから16個の周波数成分で出てきます。
■FFTのBPFの帯域幅は何で決まる?
では、この帯域幅は何で決まるでしょうか?
サンプリング周波数[fs]やサンプリング個数[N]では決まりません。BPFの幅を[Δf]とすると

Δfの逆数は丁度、FFTの処理時間「1/fs×N」と同じになります。FFTの処理区間が同じでサンプリング数が倍違うデータをそれぞれFFTして振幅を計算してみます。図からもわかるようにサンプリング周波数が倍違うことと同じことになります。

サンプリング周波数を高くしても、周波数分解能は変化しません。そこで、周波数分解能を向上したい場合はサンプリング周波数を上げるのではなくて、FFTの処理時間を長くすればいいことがわかります。
■FFT出力の周波数成分を数学的な表現で説明
今まではなるべくイメージ図で理解してもらいましたが、信号処理するときはもう少し正確さが必要になります。ここでは少しだけ数学的表現中心で説明をしたいと思います。
FFTの出力は[a]、[b]はfs/2を中心に[a]は線対称、[b]は点対称の関係(FFTの主出力成分の図を参照)になっています。32個のサンプリングデータ{0~31}をFFT計算すると以下のようになります。
a(n)=a(32-n)、b(n)=-b(32-n) 但し、0<n<16
詳しい説明は省きますが、a(0)とa(16)は実数になり、周波数的には、あまり意味を持たないと思ってください。
例えば、ある周波数、n=3の場合、a(3)=a(29)、b(3)=-b(29)と言う関係なり、複素数表現だと
n=3の周波数成分は a(3)+b(3)i
n=29の周波数成分は a(29)+b(29)i=a(3)-b(3)i
虚数部分の符号だけが反転しているこれらの周波数成分は共役な複素数関係にあると表現されます。つまり、n=3がわかればn=29の周波数成分も求められるという関係にあります。
共役な複素数とは「振幅」は同じで、「位相」の符号だけが反転している関係です。
■FFT処理時間と測定周波数の周期が不一致
サンプリング定理ではfs/2未満の周波数を取り扱えますが、取り扱う周波数がfsの整数分の1の場合が精度よく分解できます。

周期が一致してる場合はスペクトラム1本だけ正確に出てきますが、下図のように周波数が少し下がって最初と最後の値が少しずれてしまうと
ここから先は
¥ 200
最後まで読んでいただいて有難うございます。 コメントは今後の参考に、フォローやサポートは今後の励みになります。
