16進数の補数表現

どうも、とのっちょです。

ちょっとなんとなく趣味のコーディングをしていて思い出したのでちょっとメモがてらに。

16進数から10進数への変換できますか？

特になんてこともないと思うんですが、16進数から10進数への変換というのが基本情報処理でも出ると思います。コレ自体は大して難しいわけじゃなく、各桁の重みを計算して掛け算して、とかひたすら16で割っていって、とか二進数を4桁ずつに分けてとかですね。

なんで0xffff=-1なの？

Javaだと、shortに0xffffを代入して表示すると-1になります。この他にも0x7fffを代入すると32767ですが、0x8000は-32768になります。

これがなんでかっていう話です。

先頭の1ビットは符号ビット

Cではsigned intという定義と、unsigned intという定義があります。これは符号ビットを符号ビットとして使うのか、それともそのまま数として使うのか、ということなんですが、Javaにはそれがありません、全部signedです。

じゃぁ、この符号ビットが1だとなんなのかというと、負の数だ、ということになるんですが、更に落とし穴があり、負の数は補数表現というやつになります。

補数表現というのは、要は全ビット反転して1足せばいいという雑な説明になりますが、数学の勉強をしている人たちは二進数に甘えた説明を信じないでくださいね。

じゃぁ、実際に考えます。shortは2バイトの整数なので、16ビットです。0xffffは以下のようになります。

1111111111111111

先頭ビットは符号ビットなので、マイナスで、残った15この2の補数を取ると1になります。全部のビットを反転（要は全部0）にして1足すからですね。

0x7fffですが、これは、先頭ビットが0で残りが全部１ということです。

0111111111111111

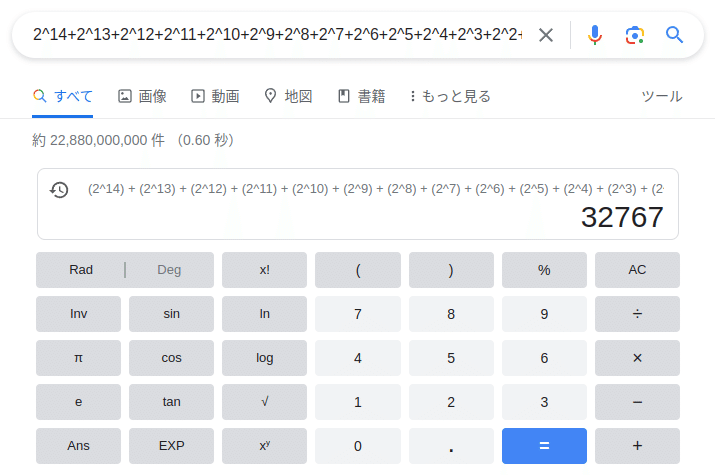
ということは、正の数であり、2^14＋…+2^0となって、32767になります。Google先生もお墨付きをくれました。

0x7fff=32767

では0x8000ですね。これは符号ビットが1でほかは全部0という状態です。

1000000000000000

ということは、15この0を反転して１を足した数ということになるので、-32768になります。2^15は32768で、符号ビットが1なのでマイナスですね。

なんで符号ビットなんて言うのがあるの？

ところでなんで符号ビットなんてあるのか、というと、要はコンピュータにはマイナスがないからです。ですが、マイナスを表現する必要があります。

なので符号ビットというのがあるみたいですね。

じゃぁなんで補数表現なんてするの？

例えば、1000...0001が-1でいいんじゃないのという話ですよね、これがなんでかというとですね、補数表現を使うと、引き算を足し算で表せるからなんですね。

16-8というのは8ですね。人間は引き算ができますが、これを足し算でやる場合は、「8の10の補数を16に足して一番上の桁を捨てる」ということをすればいいわけです。

16が2桁なので8の補数は92です。16+92=108、百の位を捨てて答えは8、というように引き算を足し算で表せるというのが補数の強みになります。

このようにすることでコンピュータは足し算さえすればいいということになります。

掛け算は複数回の足し算、割り算は複数回の引き算

で、足し算さえできれば引き算もできますし、掛け算は足し算を繰り返す、割り算は引き算を繰り替えるということになりますね。

そう考えると足し算さえできれば計算できるというのがわかる人たちってもうワケワカランですね。

そう考えると実はコンピュータは足し算しかしていないことになります。だから加算機しかないんでしょうかね。