Pythonで符号付16進数データを正負の10進数に変換（データ解析前処理）

データ解析する際、そのままでは解析できない場合が多く、たいていは解析しやすいように前処理が必要になると思います。

今回は、符号付の16進数データを、Pythonで正負の10進数へ変換する方法について書いていきます。

内容をもう少し具合的にいうと、signed（符号あり）16進数データを2進数に変換し、最上位ビット（符号ビット）で正負を判定します。符号の判定結果を用いて、正の10進数または負の10進数に変換します。この処理をPythonで行います。

こんなのどこで使うの？って思う方もいるかもしれないので、1つ事例を挙げておきます。web系のアプリケーションでは使うことがないかもしれませんが、マイコンやDSPなど組み込み系のシステムから収集したデータを扱う場合に使えると思います。

具体的な事例
蓄電システムのバッテリ充放電データを収集して、バッテリの寿命を解析する。データはRS485やCAN通信を用いて、実際に稼働している装置のマイコン計測値から収集する。通信で受け取ったデータは16進数である。バッテリは充放電するため、双方向の電流が流れるので、正負の極性がある。

いきなり本題に入る前に、基礎的なところから解説していきます。本題のプログラミングを先に見たい方は目次のリンクから先へ進んでください。

また、この記事以外にも、良い方法を知っている方がいましたら、コメントいただけると嬉しいです。

2進数・10進数・16進数

はじめに、2進数・10進数・16進数について簡単に説明します。こちらのブログが参考になると思いますので、紹介しておきます。

私たちの日常生活で最も馴染みがあるのは10進数です。10進数は「0」から「9」までの表現を扱い、10個増えたら1桁繰り上がります。世界中で一般的に使われています。

10進数
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ・・

コンピュータなどの処理には2進数が使われています。2進数は「0」と「1」だけで表現します。2個増えたら1桁繰り上がります。機械語とも呼ばれています。

使用例を挙げると、スマートフォンに搭載されているCPUで使われています。CPUは「0」と「1」だけで動いています。もっと具体的に言うと、CPUのハードウェアは電圧が閾値よりも「高い」か「低い」か、言い換えると「High」or「Low」で動作しています。

2進数
0, 1, 10, 11 ・・

マイコンのプログラミングや通信などには16進数が使われています。16進数は「0」から「F」までの表現を扱い、16個増えたら1桁繰り上がります。

個人的な感覚として、16進数は人間が日常的に扱う10進数と、コンピュータが扱う2進数の良いとこ取りのような感じです。コンピュータにとっては2進数のように扱え、人間にとっては短い桁で納まります。

16進数
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11 ・・

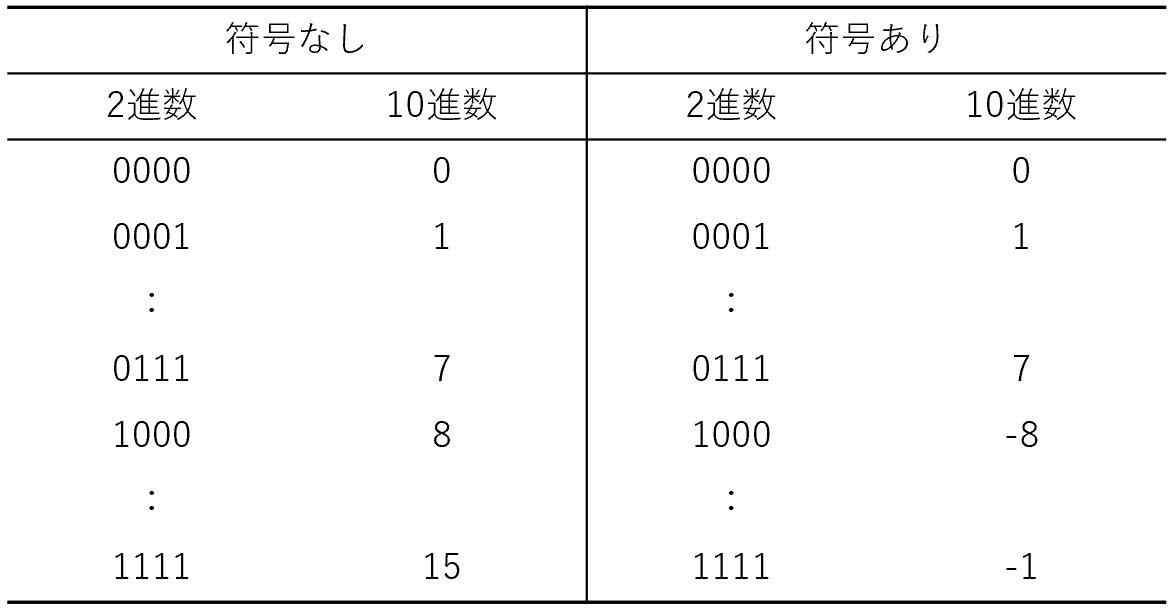
2進数、10進数、16進数を並べると下表になります。

また、知識として英語表記を覚えておくと良いです。

BIN：2進数 (binary number)
DEC：10進数 (decimal number)
HEX：16進数 (hexadecimal number)

ここまでの内容で「2進数」「10進数」「16進数」の違いと概要は把握できたと思います。ちなみに、コンピュータは正負の符号をどのように扱っているのでしょうか。次は正負の符号について解説します。

符号付データ

次はコンピュータは正負の符号をどのように扱っているのか解説します。

10進数の「2」を4ビットの2進数で表現すると「0010」になります。では、10進数で「-2」の場合はどうでしょうか。

コンピュータは「0」「1」しか表現できないので、「-」の符号は付きません。そこで、最上位のビットを「符号ビット」として扱い、最上位ビットが「0」ならば「正」、「1」ならば「負」として扱います。

ここからが重要なポイントです。

最上位の1ビットを符号として扱うので、符号なしの場合（unsigned）に対して、符号あり（signed）で扱える値は 1/2 になります。そして、2進数で「1111」が10進数で「-1」になります。詳しくはこちらのブログでも解説されています。

Pythonでデータを処理する場合、「0001」が「+1」で「1111」が「-1」になる点が重要なポイントになります。

Pythonでデータを処理する場合、最上位ビットとそれ以下のビットに分けて処理します。まず、最上位ビットで正負を判定し、次に下位のビットを10進数に変換します。

その際、負の下位ビットは2進数の「111」を10進数の「1」にする必要があります。そこで「1」と「0」を反転させるビット演算が必要になります。Pythonの「bin」や「hex」「int」を駆使して変換しようとすると「111」は「5」になってしまいます。ここが重要です。

ビット演算（AND・OR）

次は、ビット演算について解説します。ビット演算については、こちらの記事に詳しく書かれているので紹介しておきます。

まず、基本的な演算が AND と OR です。

AND（ & ）
0 = 0 & 0
0 = 0 & 1
0 = 1 & 0
1 = 1 & 1

a と b の両方に 1 が入れば c も 1

OR（ | ）
0 = 0 | 0
1 = 0 | 1
1 = 1 | 0
1 = 1 | 1

a または b のどちらかに 1 が入れば c は 1

ちょっとした注意点ですが、プログラミングの演算式は「右辺の演算結果を左辺の変数に代入する」が基本になります。日常生活で使う算数は　左から右への数式なので注意してください。

（注意）
　日常生活で使う数式
　a + b = c

　プログラミング（Python, 他）
　c = a + b

ビット演算（NOT）

次はビット演算の NOT です。NOT は 0, 1 の状態をすべて逆転させるときに使います。

NOT（ ! ）
0000 != 1111
0101 != 1010
1111 != 0000

ビット演算（XOR）

次はビット演算の XOR です。XOR は2つのデータの状態を比較して、どちか片方だけが 1 なら 1 、どちらも 0 または 1 の場合は 0 となります。2つのデータを比較して相違がある箇所を抽出するのに使えます。

XOR（ ^ ）
0000 = 0000 ^ 0000
1111 = 1111 ^ 0000
0000 = 1111 ^ 1111
0101 = 0101 ^ 0000

ビット演算（ビットシフト）

ビットシフトは格納されているデータを左右にずらします。右にずらす場合は右ビットシフト（>>）、左にずらす場合は左ビットシフト（<<）となります。

右ビットシフトの例
011110 = 111100 >> 1
001111 = 111100 >> 2

左ビットシフトの例
111000 = 111100 << 1
110000 = 111100 << 2

ビットシフトには重要な注意事項があります。

ビットシフト注意事項（超重要！）
データは格納できる数が決まっています。16ビットのデータであれば、0,1 のデータを16個までしか格納できません。よって、左右にビットシフトしてあふれた分のデータは消えてしまいます。16ビットのデータを1ビットシフトして17ビットのデータになるようなことはありません。

ここまでで「2進数」「10進数」「16進数」「符号データ」「ビット演算」について解説してきました。これらの知識をベースに、符号付の16進数データを、Pythonで正負の10進数へ変換していきます。

Pythonプログラム

Pythonの「2進数」「10進数」「16進数」相互変換については、こちらのブログで分かりやすく解説されています。

今回は8ビットの符号付き16進数データの「ff（HEX）」「-1（DEC）」を例に進めます。まず初めに、Pythonでそのまま10進数に変換してみます。ちなみに「0x」はデータが16進数であることを意味します。

16進数：ff
2進数  ：1111 1111
符号　：1 → 負
10進数：-1

ソースコード（上手くいかない例）

dataIn_Hex = '0xff'
dataOut_Dec = int(dataIn_Hex, 0)
print(dataOut_Dec)

実行結果

255

はい、違う結果になりました。
そもそも負の値になっていません。

Pythonでは符号ビットを考慮して変換してくれないので、最上位ビット（符号ビット）で正負を判定し、符号の判定結果を用いて、正の10進数または負の10進数に変換する処理が必要となります。

ソースコード

# 16進数を一旦10進数に変換し、2進数に変換
# 右にビットシフトして最上位ビットだけにする
polarity = int(bin(int(dataIn_Hex, 0) >> 7), 0)
print('極性 : ', polarity)

# 極性演算
if polarity == 1:
   # 極性が負のとき
   # 下位ビットを反転させてから10進数に変換
   dataOut_Dec = (int(bin(int(dataIn_Hex, 0) ^ 0b11111110), 0)) * (-1)
else:
   # 極性が正のとき
   dataOut_Dec = int(dataIn_Hex, 0)

# 計算結果を出力
print('変換結果 : ', dataOut_Dec)

実行結果

極性 :  1
変換結果 :  -1

これで8ビットの符号付き16進数データの「ff（HEX）」を10進数の「-1（DEC）」に変換できました。

処理を関数化して使いやすくする

次の例では、前述したコードを関数化して使いやすくしていきます。例えば以下のように関数化しておけば繰り返し使う場合にとても便利です。