Python-Control 電流フィードバック制御系の特性比較

Pythonの制御工学ライブラリであるPython-Controlを自動制御システムの設計計算に活用してみようと取り組んでいます。本記事ではフィードバック制御の簡単な例として、電気回路のRL回路で電流フィードバック制御の特性を Python-Control で出力してみます。

また、コントローラの制御パラメータを変化させてボード線図の違い、ステップ応答の違いを見てみます。その結果から、制御ゲインをどのように与えたら、どのような特性になるのか考察したいと思います。

今回はフィードバック制御の流れを掴む事を目的とし、制御モデルもできる限り簡単にして進めていこうと思います。

開発環境

・windows 10（64bit）
・Visual Studio Code 1.45.1
・Python 3.8.2（32bit版）

そもそも RL 回路ってなに？

ご存じの方は読み飛ばして頂いても構いません。

RL 回路は抵抗（Resistance）とインダクタ（Inductor）を組み合わせた電気回路です。インダクタはコイル（電線をグルグル巻いたもの）です。理科の実験で見たことがあると思います。

インダクタはあらゆる電気機器で使われており、バッテリの充放電を制御する回路などにも使われています。ここでは詳細を説明しませんが、インダクタには以下の特徴があります。この特徴を活用して、抵抗とインダクタを組み合わせて回路の電流を制御します。

ちなみに、インダクタの回路シンボルとして「L」が使われるのには諸説あるようですが、電磁誘導に関する「レンツ(Lenz)の法則」に由来しているようです。

インダクタの特長
・インダクタに流れる電流が増加するとそれを妨げようとする
・インダクタに流れる電流が減少するとそれを増加させようとする

RL 回路の電流制御で何ができる？

RL 回路の電流制御ができれば、バッテリ充放電の電流を制御できます。他にも、モータの制御に展開できます。モータも大まかにいえばコイルなので、巻いている電線の抵抗分を含めて、RL 回路のモデルで置き換えることができます。

バッテリの充放電、モータの制御と言ったら「電気自動車」ですね。実際には、他にも色々な制御系が必要ですが、電気自動車の自動制御に展開できます。

（余談：モータの速度制御）
モータ制御の場合、電流フィードバック制御ループの外側に速度制御フィードバック制御ループを構成することで、モータの回転速度を制御できるようになります。速度制御のコントローラが、与えられた速度指令とセンサで検出した実際のモータ回転速度の偏差に応じて操作量を演算し、演算結果がモータに流す電流指令値になります。

そしたら今度は速度制御系の内側にある電流制御フィードバック制御ループで、電流制御のコントローラが電流を制御します。世の中にある自動制御システムの多くは、このように何重ものフィードバック制御ループで構成されています。

制御するシステムの構成

システムの自動制御を行うにあたり、まず初めに行うのが制御対象のモデル化です。そのためには制御するシステムの構成を把握する必要があります。今回、フィードバック制御するシステムは下図とします。少々図が雑なのはご了承ください。

抵抗 R とインダクタ L 、直流電圧源 Vs で構成された回路がベースになります。しかし、R, L, Vs だけだと回路に流れる電流はオームの法則から I＝Vs/R となり一定の電流しか流れません（インダクタは直流に対してインピーダンスがゼロになるため Z＝jωL＝j2πfL ）。

そこで登場するのがスイッチ（SW）です。この回路にスイッチを挿入し、スイッチを ON/OFF することで、抵抗RとインダクタLの両端電圧 VRL を 0 または Vs に変化させます。こうすることで RL 回路に流れる電流を制御します。

また、電流を制御するためにはセンサを使って現在流れている電流を検出し、コントローラにフィードバックする必要があります。なので、制御したい対象に応じて必要なセンサを入れます（例：電流センサ、電圧センサ、速度センサなど）。

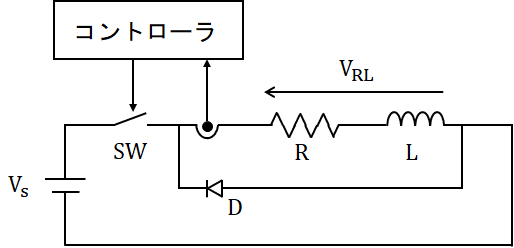
ちなみにダイオード D が入っているのは、インダクタ電流が還流する経路を作るためです。先ほど、インダクタは流れる電流が減少するとそれを増加させようとする特性があると記載しました。

今回の場合、スイッチ（SW）を OFF すると、インダクタは磁気的に蓄えられたエネルギーで電流を流し続けようとします。そのため、インダクタの電流の行き場を作ってあげます。インダクタの電流の行き場を作ってあげないと、インダクタの両端電圧が跳ね上がってしまい、回路の破損に繋がります。また、一般的にスイッチ（SW）にはトランジスタや IGBT といった半導体部品が使われます。

（余談：PWM 制御）
スイッチを ON/OFF するだけで、どうして電流を制御できるのか疑問を抱く方がいるかもしれません。スイッチを ON/OFF して RL の両端に 0 または Vs の電圧を加えるだけなのにどうして電流を制御できるのか。

細かく解説すると、スイッチを ON させる時間と OFF させる時間の比率にポイントがあります。スイッチ ON の時間と OFF の時間を合わせて1周期とし、その1周期間において、ON 時間を50%、OFF 時間を50%とした場合、RL の両端に印加される電圧は平均すると 0.5Vs となります。

もし ON 時間が80%、OFF 時間が20%であれば RL の両端に印加される電圧は平均すると 0.8Vs となります。つまり、スイッチ（SW）の ON 時間と OFF 時間の比率を制御することで、RL の両端には平均的に 0～Vs の電圧を印加することができるのです。

これをPWM（Pulse Width Modulation）制御といいます。RL の両端に印加する電圧パルス（0, Vs）の幅（ON時間とOFF時間）を変調させてあげるのです。

システムのモデル化

制御するシステムの構成を把握出来たら、次はシステムをモデル化して伝達関数を導出します。本来ならば、スイッチの部分もモデル化する必要があるのですが、今回はできる限り簡単なモデルでフィードバック制御の流れを掴む事を目標にしているので省略します。

現実的には、他のモデルよりも十分に応答が早ければ無視してもシステムの特性に大きな影響は生じないです。とりあえず今回は、RL 回路の部分とコントローラだけをモデル化します。

RL 回路部
RL 回路部の伝達関数は電圧方程式から次式になります。抵抗 R とインダクタ L のインピーダンス、両端電圧 VRL(s) と電流 I(s) の方程式を解きます。

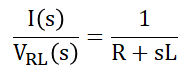
コントローラ部
今回、コントローラには PI 制御（比例積分制御）を使いたいと思います。ここは P 制御でも PID 制御でも問題ないですが、それぞれに良し悪しがあります。PI 補償器の伝達関数は次式になります。比例ゲインを Kp とし、積分ゲインを Ki とします。

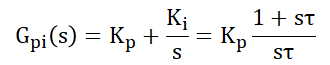
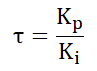
ブロック図

システムをモデル化できたら、導出した伝達関数を組み合わせてブロック図を作成します。これまでに導出した伝達関数を組み合わせると下図になります。PI 補償器に電流目標値と検出値の偏差を入力します。PI 補償器の出力として操作量が出てきます。この操作量によって RL 回路に印加される電圧が変化し、RL 回路に流れる電流が目標値に制御されます。また、PI 補償器はコントローラと呼び、制御対象の RL 回路はプラントと呼びます。

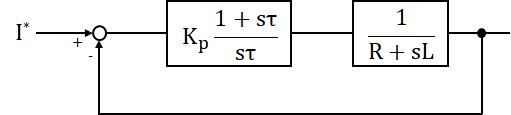
ブロック線図から閉（Closed）ループの伝達関数を計算すると次式になります。

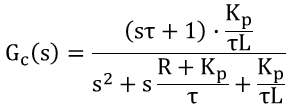
この数式をよく見ると、1次進み系の伝達関数に2次系の伝達関数が組み合わさった数式になっています。2次系の伝達関数はよく次式で表されます。

先ほどの数式に照らし合わせると、ζ と ωn は次式になります。2次系であることから、Kp と Ki の設計次第ではオーバーシュートのない1次遅れ的な特性になりますし、オーバーシュートする振動的な特性にもなります。

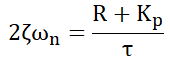
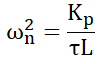
ボード線図

Python-Control を使ってボード線図を出力します。まず RL 回路の伝達関数のボード線図は下図になります。各パラメータは下記の値としました。まずは下記のパラメータでボード線図を出力し、そのあとに制御部の積分ゲインを変化させてボード線図を出力してみます。

パラメータ
　R ＝ 5mΩ
　L ＝ 10mH
　Kp ＝ 1.0
　Ki ＝ R/L

RL回路部のボード線図
角周波数は ω＝R/L＝2πf となるので、折点周波数は 0.08Hz 付近になります。折点周波数はゲインが -3dB 低下したところの周波数になります。出力したボード線図でも 0.08Hz で -3dB 低下しています。折点周波数より高周波数領域になると位相が -90° まで低下していきます。

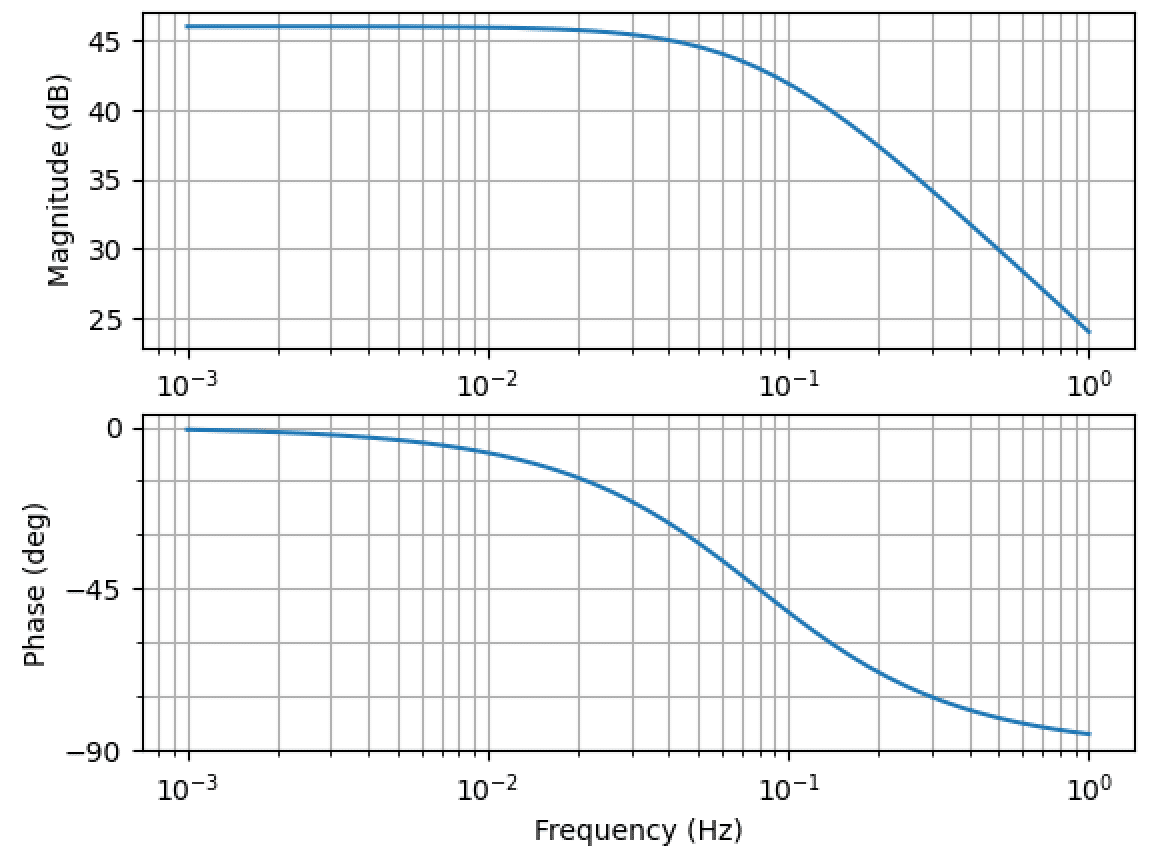
PI制御器のボード線図
上記のように、比例ゲイン Kp は 1.0、積分ゲイン Ki は R/L としています。角周波数は ω＝1/τ となり、前述した数式より τ＝Kp/Ki なので折点周波数は RL 回路と同様に 0.08Hz となります。

PI 補償器は折点周波数より低周波数領域ではゲインが高く、位相は -90° になっています。このボード線図から、制御対象である RL 回路の折点周波数に対して、コントローラの折点周波数を高周波数領域または低周波数領域のどちらにもっていくかでシステムの制御特性が変わります。

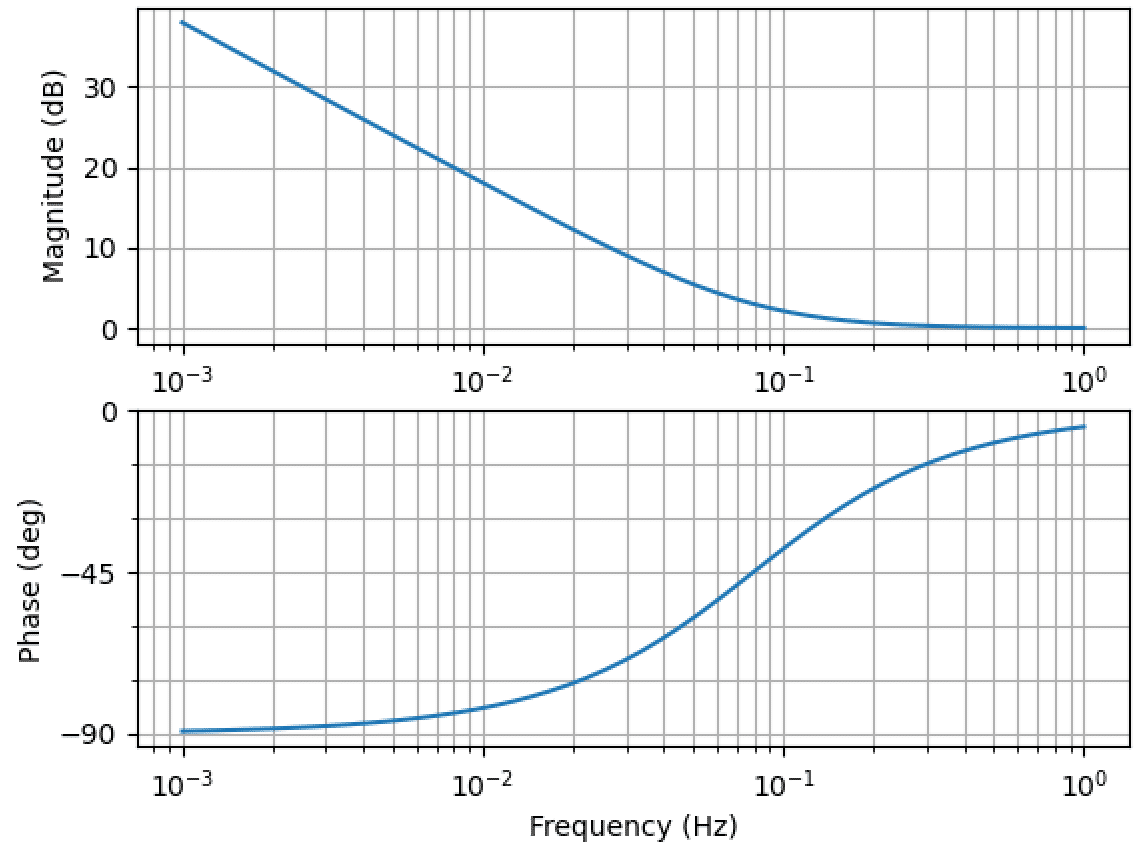
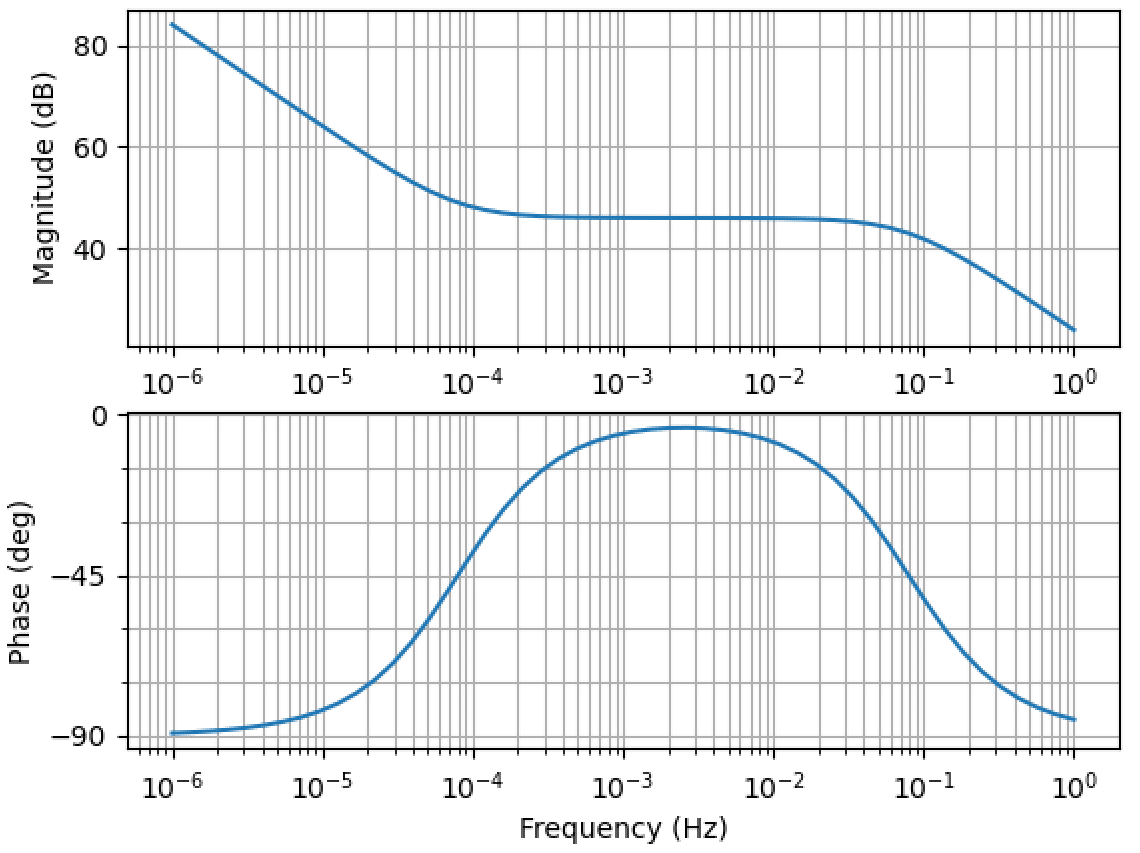
開ループ伝達関数（Ki＝R/L）
上記のパラメータで開（Open）ループ伝達関数のボード線図を出力すると下図になります。周波数によらず、ゲインは -20dB で低下し、位相は -90° で一定となります。

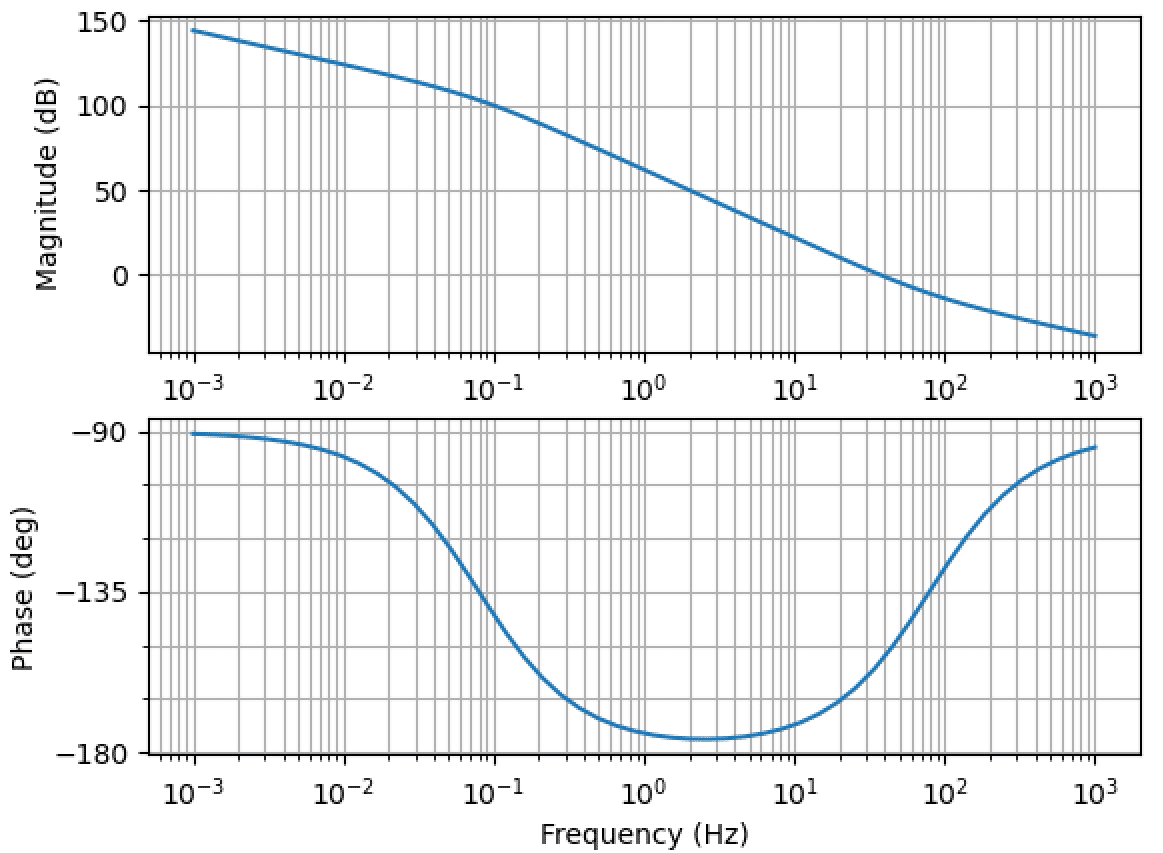
開ループ伝達関数（Ki＝(R/L)×1000）
コントローラの積分ゲイン Ki を 1000 倍にしました。RL 回路の折点周波数に対して、コントローラの折点周波数は 1000 倍になります。そうすると 0.1Hz 〜 100Hz 付近の帯域でゲインは -40dB で低下し、位相は -180° 付近まで低下します。Ki＝R/L の時と比較して位相余裕は少なくなることが分かります

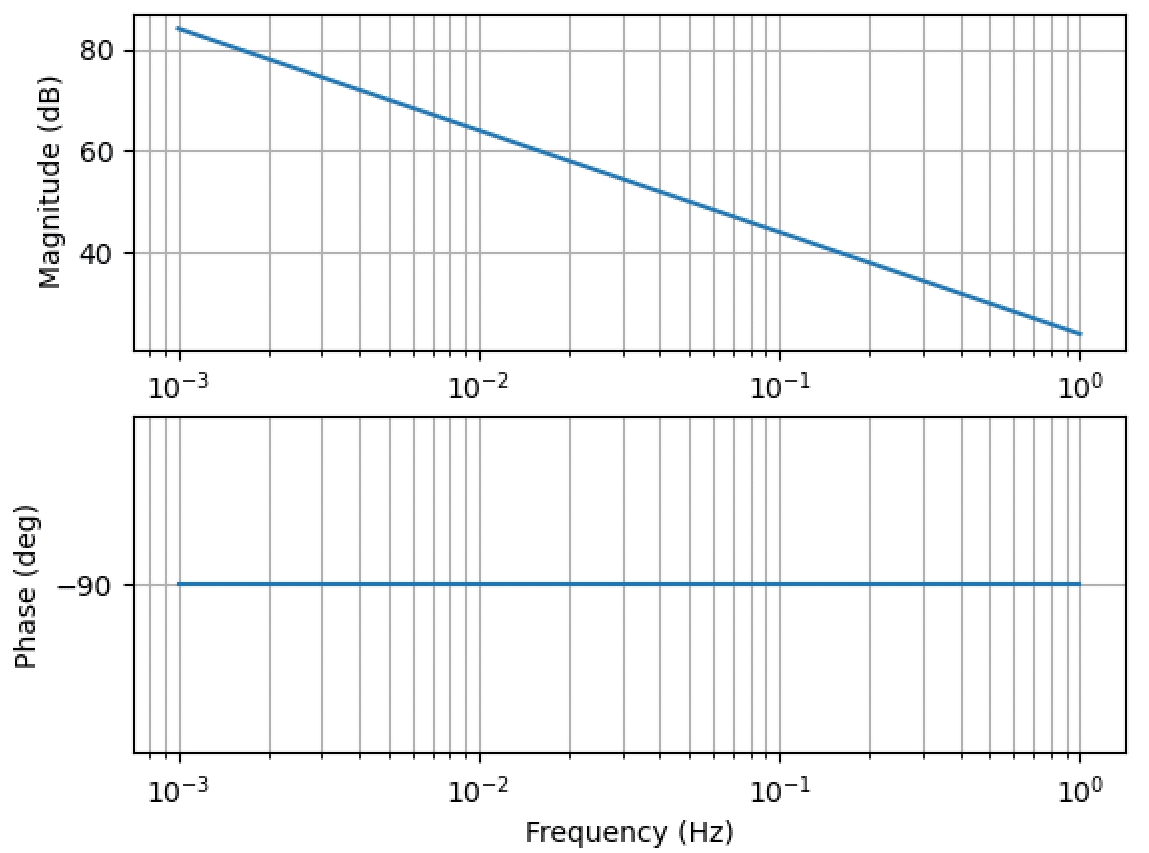
開ループ伝達関数（Ki＝(R/L)×0.001）
コントローラの積分ゲインを 1/1000 倍にしました。RL 回路の折点周波数に対して、コントローラの折点周波数は 1/1000 倍になります。そうするとゲインが低下しない周波数帯域が生じ、位相は 0° 付近まで変化する周波数帯域が生じます。

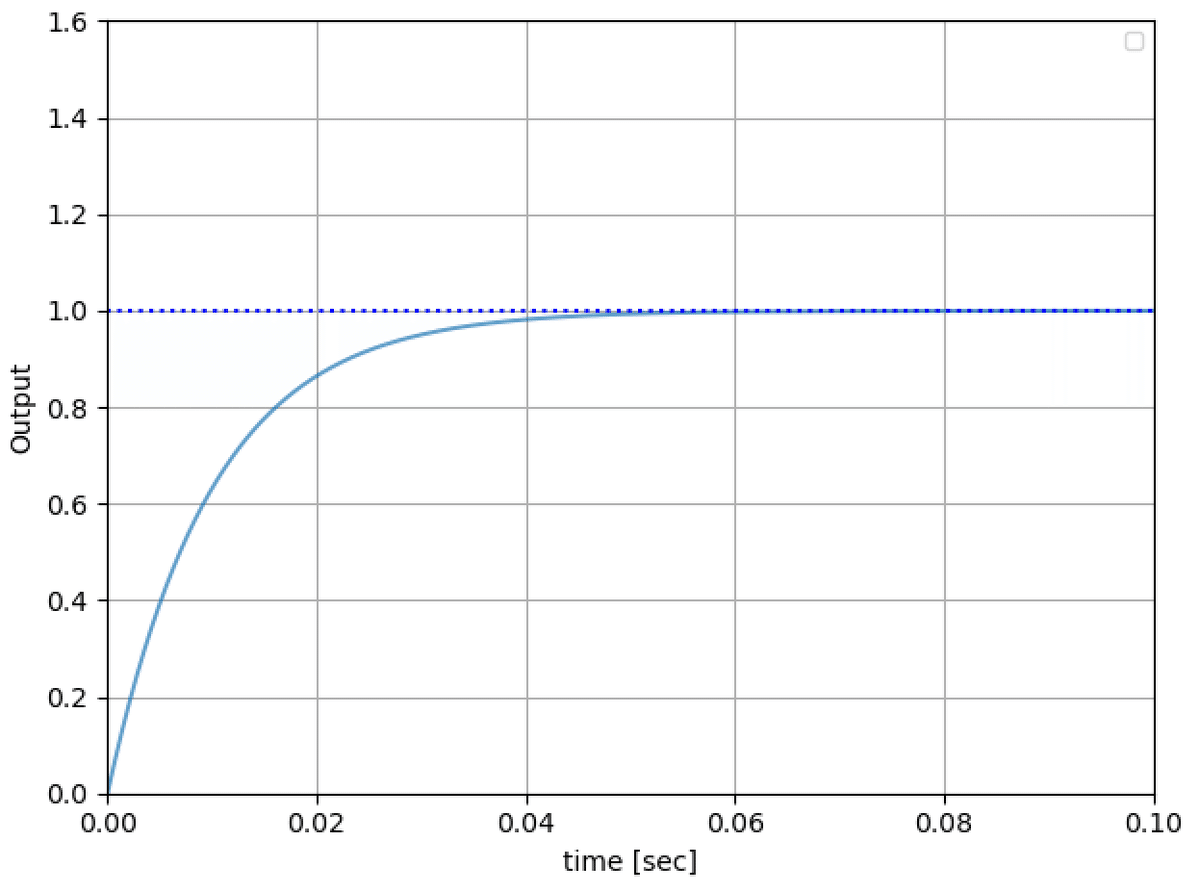
ステップ応答

次にステップ応答を出力してみます。

Ki＝R/L
ステップ応答は1遅れ系になり、オーバーシュートも振動も見られません。応答波形は 0.04sec 程度でほぼ収束します。この場合、閉ループ伝達関数は１次遅れ系に近似しても問題ありません。近似する事のメリットとして、何重ものフィードバック制御で構成されたシステムを設計するときに計算が楽になります。

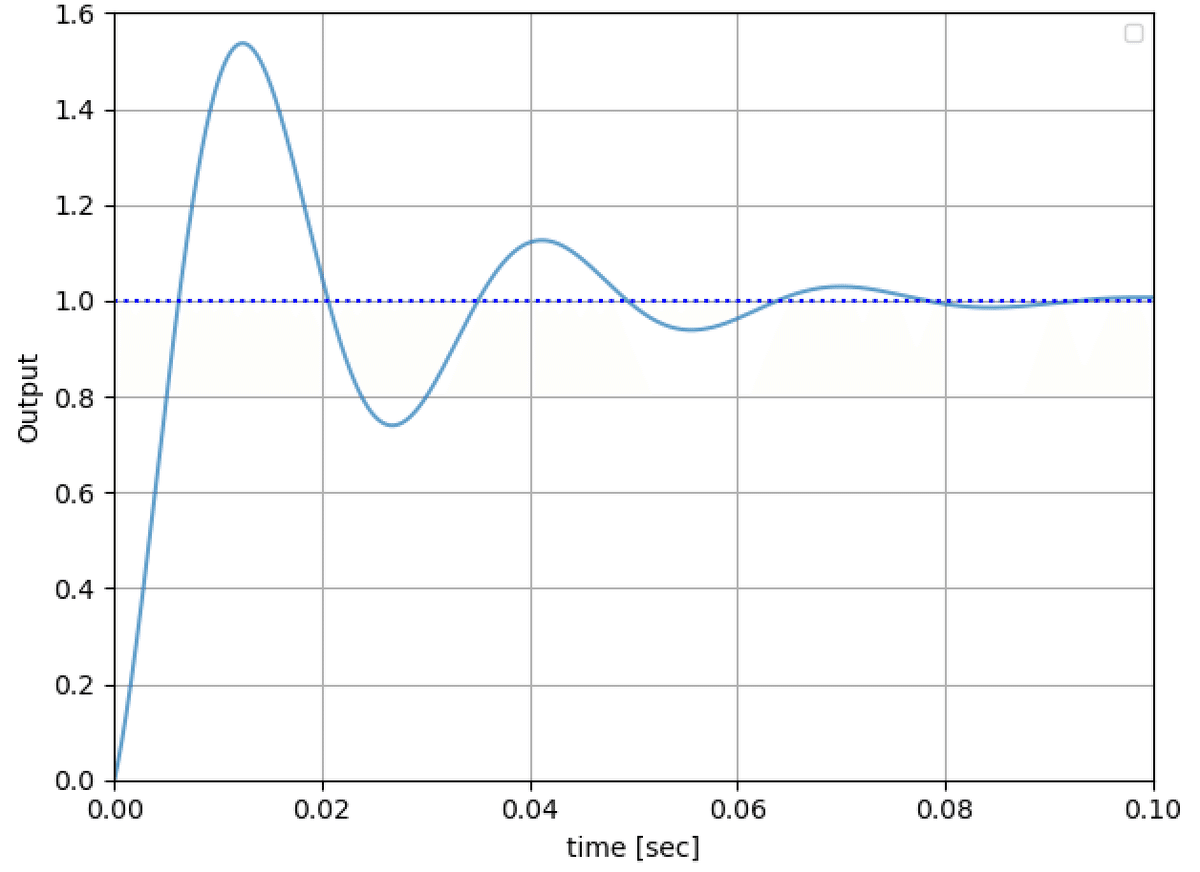
Ki＝(R/L)×1000
ステップ応答に、ピークで +50% 程度のオーバーシュートが生じ、波形は振動的になります。波形はちゃんと収束していますが、システムの特性を振動させたくない場合は改善が必要になります。

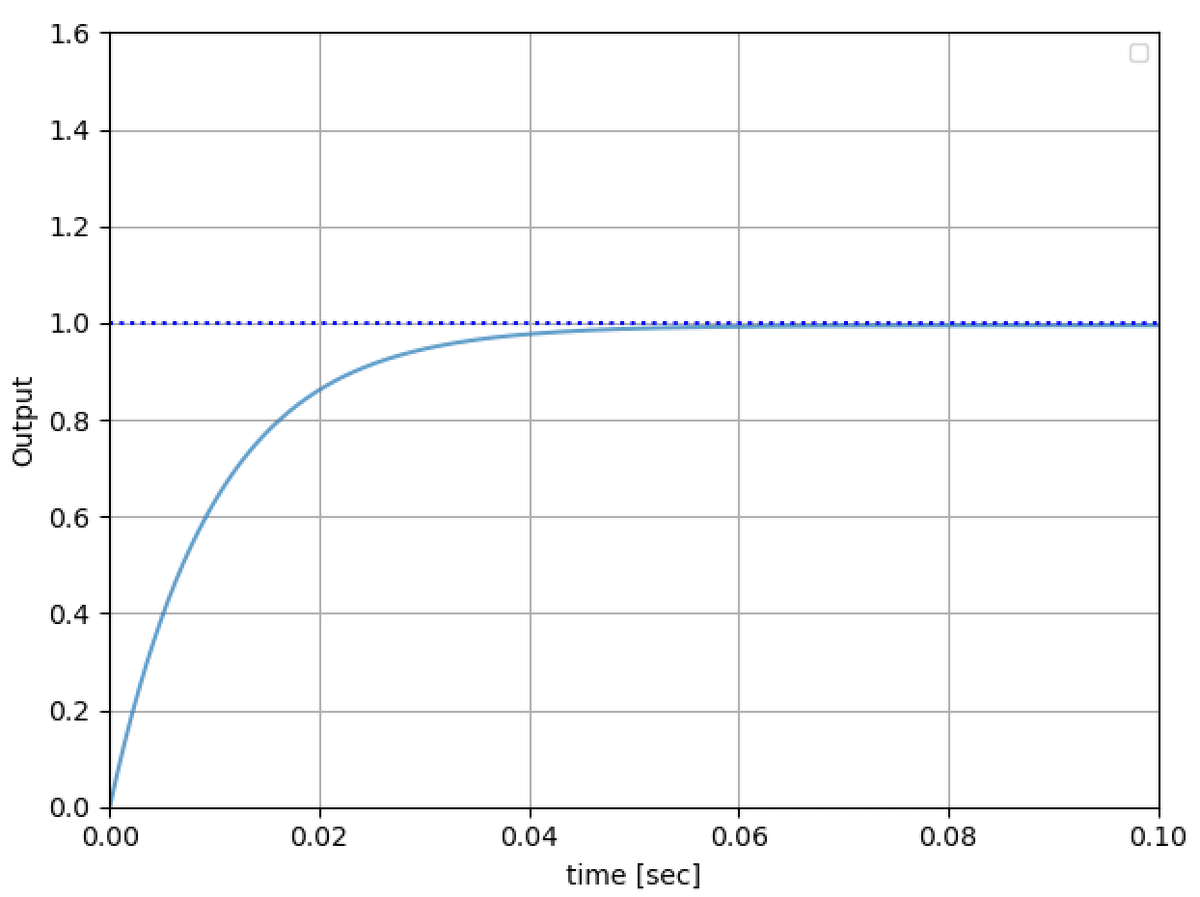
Ki＝(R/L)×0.001
ステップ応答は1遅れ系になり、オーバーシュートも振動も見られません。応答波形は 0.04sec 程度でほぼ収束します。Ki＝R/L の時と同様の特性になりました。

まとめ

電気回路の RL 回路で電流フィードバック制御の特性を Python-Control で出力しました。コントローラの制御パラメータを変化させてボード線図の違い、ステップ応答の違いを確認した結果、積分ゲイン Ki を大きくしていくと振動的な特性となり、小さくしていくと１次遅れ系の特性となることが分かりました。

制御ゲインの与え方次第で、オーバーシュートのない1次遅れ的な特性になりますし、オーバーシュートする振動的な特性にもなるということが分かりました。余談として、ステップ応答波形が収束していれば振動的な特性でも一応問題はありません。

しかし、現実的なシステムの制御を考えた場合、電流フィードバック制御ループの外側に、電圧フィードバック制御や速度フィードバック制御を構成するため、外側のフィードバックループの設計をする際に安定性が低下して設計に苦労すると思います。なので、何重にもフィードバックループが構成されるシステムにおいて、最も内側に構成されるフィードバックループは、オーバーシュートするかしないかくらいの特性で設計するのが良いと思います。

Python ソースコード

Python のソースコードを以下に添付します。classの部分については過去に作成したこちらの記事をご参照ください。

# =================================================
#           ライブラリインポート
# =================================================
# 数値演算ライブラリ
import numpy as np
# 制御工学ライブラリ
from control import matlab
# グラフ描画
from matplotlib import pyplot as plt

# =================================================
#           固定パラメータ
# =================================================
# ステップ応答時間設定
TIME_START = 0.0
TIME_END = 0.1
TIME_STEP = 1000

# 回路パラメータ
R = 0.005
L = 0.01

# =================================================
#           class定義
# =================================================
# クラス定義 (伝達関数モデル作成)
class tf_model:

   # 初期化メソッド
   def __init__(self):
       # ゲイン 1.0 の比例要素に初期化
       num = [1.0]
       den = [1.0]
       self.tf = matlab.tf(num, den)

   # 1次遅れ要素
   def delay_1st(self, k, t):
       num = [k]
       den = [t, 1]
       return matlab.tf(num, den)

   # PI補償器
   def controller_pi(self,kp, ki):
       # 比例補償器
       num_p = [kp]
       den_p = [1]
       Gp = matlab.tf(num_p, den_p)
       # 積分補償器
       num_i = [ki]
       den_i = [1, 0]
       Gi = matlab.tf(num_i, den_i)
       return Gp + Gi
 
# =================================================
#           関数
# =================================================

# =================================================
#           メイン
# =================================================
 #インスタンス生成 
temp_tf = tf_model()

# RL回路の伝達関数
G_RL = temp_tf.delay_1st(1/R, L/R)

# ボード線図作成
matlab.bode(G_RL)
plt.show()

# PI補償器のの伝達関数
Gpi = temp_tf.controller_pi(1.0, R/L)

# ボード線図作成
matlab.bode(Gpi)
plt.show()

# 開ループ伝達関数
Go = Gpi*G_RL

# ボード線図作成
matlab.bode(Go)
plt.show()

# 閉ループ伝達関数
Gc = matlab.feedback(Go, 1.0)

# ステップ応答
t = np.linspace(TIME_START, TIME_END, TIME_STEP)
(output, t) = matlab.step(Gc, t)

# 波形出力パラメータ
# (ls:線種, lw:線太さ, alpha:透過度, color:色指定, marker:マーカー形状指定, ms:マーカーサイズ, label:凡例名)
plt.plot(t, output, alpha=0.7)

# 収束値を点線表示
plt.axhline(1.0, ls=":", color="blue")

# グラフ表示設定
plt.rcParams['font.family'] = 'Times New Roman' # 全体のフォント
plt.legend(loc="upper right",fontsize=8)        # 凡例の表示（2：位置は第二象限）
plt.xlabel('time [sec]', fontsize=10)           # x軸ラベル
plt.ylabel('Output', fontsize=10)               # y軸ラベル
plt.xlim([0, TIME_END])                         # x軸範囲
plt.ylim([0, 1.6])                              # y軸範囲
plt.tick_params(labelsize = 10)                 # 軸ラベルの目盛りサイズ
plt.tight_layout()                              # ラベルがきれいに収まるよう表示
plt.grid()                                      # グリッド表示
plt.show()                                      # グラフの表示

以上