
数学×ミリシタ 第1講「二項分布」;目的の提供割合が1%のガシャを100回引いたとき、目的が排出される確率は?
こんにちは。大学生(学士課程)です。いつもは嘘を申し上げる文章を書いている者ですが、今回は全て真実を述べます。そのため、本文中に誤りを発見された場合はご一報ください。
導入「ガシャとは?」
※ガシャのことをご存じの方は、読み飛ばしてください。
一般的に、スマートフォンやPCなどのゲームにおいて、「基本無料(一部有料アイテムあり)」のような表記があるものにありがちなシステムであり、そのゲームの進行において有利になるアイテムや、衣装や装備を入手する手段を一般的に「ガチャ」と言う。なお、ゲームを配信している企業によっては、ガチャを「ガシャ」と表記をする場合がある。……と、こんなこと言っても、知らない人にはわかりづらい内容であるため、はっきりと申し上げます。ガチャを知らない人は今すぐに、この文章を読むことをやめなさい。ガシャとは、法の裁きを受けない危険薬物のようなものであり、手を出していない人物が手を出す事自体が危険である。
ミリシタにおけるガシャ
みなさんはご存知でしょうか。バンダイナムコエンターテインメントによる、主にスマートフォンで展開されるゲーム「アイドルマスター ミリオンライブ! シアターデイズ」(略:ミリシタ)を。

ミリシタも例に漏れず、ガシャというシステムが存在します。ミリシタにおいて、ガシャは数種類存在しますが、今回は「プラチナガシャ」を取り上げます。プラチナガシャは、一定期間ごとに新規SSRのアイドルのカードが追加され、追加されたカードは、排出率がほかのSSRのカードよりも高く設定されている、いわゆる「ピックアップ」の対象となります。
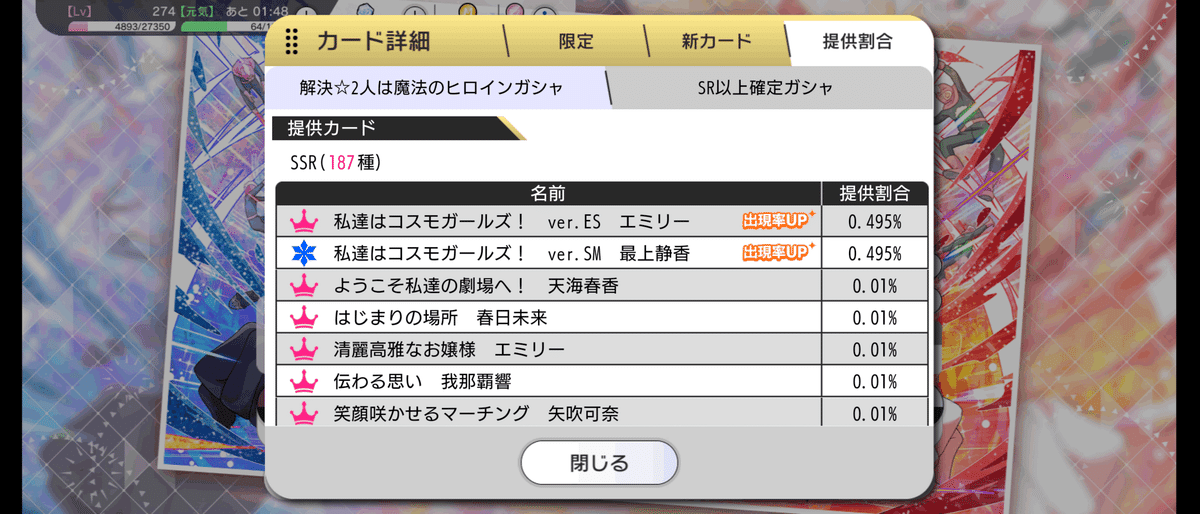
図2は、執筆当時に実施されているプラチナガシャの提供割合です。図内の表において、上から2名が今回のピックアップです。図を見てわかる通り、ピックアップ対象は、ほかのSSRカードと比較して排出率が高いです。また、ガシャを300回引くと、任意のピックアップカードを選択して入手することができる通称「天井」というシステムが存在します。
目的の提供割合が○○%のとき、目的が排出される確率は?
1 目的の提供割合が1%のとき、ガシャを100回引いて目的が排出される確率は?
この記事の副題でもあるように、目的の提供割合が1%のときを考えましょうてみましょう。

少し古いですが、図3のように、2020年12月25日~12月31日までに実施された、ミリオンフェスのときについて考えてみましょう。このガシャは1日10連1回、計60回分を無料で引くことができました。このとき、ピックアップカードの提供割合はいずれも0.99%であります。
ここで、例えば佐竹美奈子さんのPさんがこのガシャを引くことを考えてみましょう。このPさんは、「小さな燈火 佐竹美奈子は確実に欲しい。芥の恋 真壁瑞希は引ければラッキー」「ミリオンジュエルは10000個のみ所持(=40連分)、無料60連、計100連で挑む」という状況としましょう。
ここでは簡単のため、「小さな燈火 佐竹美奈子」の提供割合が1%のときを考えます。提供割合が1%のとき、100回引いて少なくとも1回「小さな燈火 佐竹美奈子」が排出される確率はどれくらいになると思いますか?これを読んでいるみなさんも、「提供割合が1%のとき、100回引けば1回くらいは必ず出る」という考えを持つ人は多くはないでしょう。正解です。では具体的な確率はどれくらいでしょうか。50%くらい?90%くらい?
正解は、およそ63.4%です。「思ったより少ない」と思う方も一定数いるかもしれません。現実とはそういうものなのです。
2 63.4%を簡単に運試しする方法
身近な63.4%を調べてみました。スキルLvが3のカードに対してレッスンチケット Rを15枚使用すると、スキルLv上昇確率は64%です。

また、スキルLvが4のカードに対してレッスンチケット Rを19枚使用すると、スキルLv上昇確率は63%です。

人間のガシャ欲というものはこんなものでは満たされないことはわかっています。しかし、これに効く薬はありません。
3 目的の提供割合が○○%のとき、ガシャを△△回引いて目的が排出される確率は?
2023年2月現在、ミリシタのプラチナガシャにおけるピックアップカードの提供割合は主に、
①SONG FOR YOU!ガシャ(恒常ガシャ)期間限定ペアガシャ(髪色変化)が各ピックアップごとに0.495%
②ミリオンフェス(ピックアップが3枚のとき)が各ピックアップごとに0.66%(画像なし)
③セカンドヘアスタイルガシャ~プライベートドレス編~が各ピックアップごとに0.899%

④ミリオンフェス(ピックアップが2枚のとき)および限定復刻ガシャが各ピックアップごとに0.99%
となっています。
目的の提供割合が以上のとき、ガシャを数回引いて目的が排出される確率は以下の通りになります。

各提供割合において、目的が排出される確率が50%以上のとき、確率の値を色付けしています。
①提供割合が0.495%のとき、140回以上引くことで、排出される確率が50%を超え、天井となる300回時点で、排出される確率は77.4%となります。つまり、22.6%で天井します。
②提供割合が0.66%のとき、105回以上引くことで、排出される確率が50%を超え、天井となる300回時点で、排出される確率は86.3%となります。天井する確率は、13.7%となります。
③提供割合が0.899%のとき、77回以上引くことで、排出される確率が50%を超え、天井となる300回時点で、排出される確率は93.3%となります。よって、天井する確率はおよそ6.7%です。
④提供割合が0.99%のとき、70回以上引くことで、排出される確率が50%を超え、天井となる300回時点で、排出される確率は94.9%となります。天井する確率は、5.1%ほどです。
4 確率の求め方
それでは、上の図のような確率はどのように求められるのかを教授します。仕組みを理解すれば、自分で任意の提供割合において、任意の回数ガシャを引くとき、目的が排出される確率を求められます。
・$${n}$$ 回ガシャを引き、提供割合が $${p}$$ % のカードを1回以上排出される確率(単位は%)は
$$
\left\{ 1- \left( 1- \frac{p}{100} \right)^n \right\} \times100
$$
となることが知られています(導出は後述します)。
例えば、以下のシチュエーションについて、実際に計算してみましょう。

図8のガシャを引きたいとします。いま、ミリオンジュエルを24,500個所持しており、ガシャは98回引くことができます。何としてもこのガシャのピックアップカードの1つである「JUSTICE!AKANECHAN! 野々原茜」を引きたいとします。スクショは取っていませんが、このガシャは限定ガシャであり、「JUSTICE!AKANECHAN! 野々原茜」の提供割合は0.495%です。このガシャを98回引くとして、「JUSTICE!AKANECHAN! 野々原茜」が排出される確率を一緒に求めてみましょう。
($${n}$$=98) 回ガシャを引き、提供割合が ($${p}$$=0.495) % のカードが1回以上排出される確率(単位は%)は、
$$
\left\{ 1- \left( 1- \frac{p}{100} \right)^n \right\} \times100
$$
に($${n=}$$98) と ($${p=}$$0.495) を代入して、
$$
\left\{ 1- \left( 1- \frac{0.495}{100} \right)^{98} \right\} \times100
$$
となります。なお、この計算を手で行うことは困難です。計算機を使いましょう。
今回は、一番簡単な「関数電卓」を用いた求め方を初心者向けに教授します。はじめに、関数電卓を用意します。WindowsやGoogleなどで「関数電卓」と検索すると、関数電卓を使用できます。

まずは、計算の順序に従い、
$$
\left( 1- \frac{0.495}{100} \right)^{98}
$$
を計算します。計算機に、「(1-(0.495/100))^98」と順に入力します。「^」は累乗$${^{98}}$$を表します。計算機によると、結果は「0.614894…」となります。今回は小数点第5位で四捨五入して、0.6149としましょう。すると、最初の式は、
$$
\left( 1- 0.6149 \right) \times100
$$
となり、これを計算すると、
$$
=0.3841 \times100
$$
$$
=38.51
$$
という結果になります。したがって、提供割合が0.495%の目的「JUSTICE!AKANECHAN! 野々原茜」のガシャを98回引くとして、排出される確率は、およそ38.5%であることが求められました。この38.5%という数字が大きいと考えるか、小さいと考えるか、98回引く価値はあるか、それは自分自身の問題です。確率は目安でしかありません。
なお、上記以外の提供割合で、抽選回数について計算するときは、0.495と98を変えることで、任意の確率を求めることができます。
順序の復習です。
1 (提供割合) ÷ 100 を計算する
2 1の計算結果を (ガシャを引く回数) 乗する
→ (1の計算結果)^(ガシャを引く回数)
3 1から、2の計算結果を引く
(4 3の計算結果を100倍すると、確率の単位は%になります。)
この計算になれたい人がいましたら、次の例題を解いてみてください。(1)~(4)の解答はこの記事の下の方にあります。
例題
次の問いに答えてください。なお、答えの表記は問いません(%表記でも可)。
(1) 目的の提供割合が0.495%のとき、ガシャを78回引いて、目的を1回以上引き当てる確率は?
(2) 目的の提供割合が0.899%のとき、ガシャを5回引いて、目的を1回以上引き当てる確率は?
(3) 目的の提供割合が0.99%のとき、ガシャを26回引いて、目的を1回以上引き当てる確率は?
(4) 目的の提供割合が0.495%のとき、ガシャを85回引いて、目的を1回以上引き当てる確率は?
(5) 現在実施しているガシャについて、今持っているミリオンジュエルをすべて使ってガシャを引くとき、ピックアップSSRのうちの1枚が1回以上引き当てる確率は?
5 式の導出・二項分布
第4項において、
$${n}$$ 回ガシャを引き、提供割合が $${p}$$ % のカードが1回以上排出される確率(単位は%)は
$$
\left\{ 1- \left( 1- \frac{p}{100} \right)^n \right\} \times100
$$
と紹介しました。この式の導出を紹介していきます。
起こりうる出来事が {A, B} のみであるとき、Aが起こる確率を $${p}$$ とします。起こりうる出来事は {A, B} のみであるため、Aが起こらないということは、必ずBが起こることになります。したがって、Bが起こる確率は、100%からAが起こる確率を引き、$${1-p}$$であることがわかります(確率の公理主義的定義)。この不変の条件のもと、{A, B} のどちらかを独立に抽選することを繰り返すことを、Bernoulli試行(ベルヌーイ試行)と言います。Bernoulliとは、人名 Jakob Bernoulliさんのことです。
例えば、ガシャにおいて起こりうる出来事は、{目的が排出される, 目的が排出されない} の2通りであるときを考えます(目的がない場合は考えないことにします)。目的が排出される確率を、今回は$${p}$$とします。片や、目的が排出されない確率は、1-(目的が排出される確率)であり、$${1-p}$$です。例えば、目的の提供割合が0.99%のとき、$${p=}$$0.0099で、$${1-p=}$$0.9901です。
この条件のもとでガシャを引くことは、Bernoulli試行と言えます。
※なお、引けば引くほど確率が変わるガシャ(例:ミリコレのコインガシャ)は、独立ではないため、Bernoulli試行ではありません。
Bernoulli試行を$${n}$$回行うとき、すなわち、ガシャを$${n}$$回引くとき、目的が$${x}$$回排出される確率は、
$$
p^x
$$
であり、目的が排出されない回数は、(ガシャを引いた回数)-(目的が排出された回数)であり、$${n-x}$$回です。よって、$${n-x}$$回目的が排出されない確率は、
$$
(1-p)^{n-x}
$$
です。$${n}$$回ガシャを引く中で、$${x}$$回の目的の排出、$${n-x}$$回の目的が排出されないという出来事が起こる組合せがあります。この組合せは、$${_n\text{C}_x}$$通りあります。
$${_n\text{C}_x}$$は、二項係数とよび、一般的に$${\binom{n}{x}}$$と表記します。
※ $${_n\text{C}_x}$$の求め方は、付録を確認してください。
以上をまとめて、目的の排出確率が$${p}$$のBernoulli試行を$${n}$$回行い、目的が$${x}$$回排出される確率は、
$$
f(x)=\binom{n}{x}p^x(1-p)^{n-x}
$$
という$${x}$$を確率変数とする確率関数で表される確率分布に従うとされ、この確率分布を二項分布と言います。
例えば、目的の排出確率が0.99%のBernoulli試行を100回行い、目的が2回排出される確率は
$$
f(2)=\binom{100}{2} \times\left(\frac{0.99}{100}\right)^2\times\left(1-\frac{0.99}{100} \right)^{100-2}
$$
で求められます。これを用いて、$${n}$$ 回ガシャを引き、提供割合が $${p}$$ % のカードを1回以上引き当てる確率を求めていきます。ガシャにおいて、目的のカードが1回以上排出される確率は、1-(目的のカードが1回も排出さない確率)と同義です。
目的のカードが1回も排出さない確率は、
$$
f(0)=\binom{n}{0} \times\left(\frac{p}{100}\right)^0 \times\left(1-\frac{p}{100} \right)^{n-0}
$$
となります。ここで、
$$
\binom{n}{0} = \left(\frac{p}{100}\right)^0 =1
$$
を利用して、
$$
f(0)=\left(1-\frac{p}{100} \right)^n
$$
となります。したがって、目的のカードが1回以上排出される確率は、
$$
1-f(0)
$$
$$
=1- \left( 1- \frac{p}{100} \right)^n
$$
単位を%にすると、
$$
\left\{ 1- \left( 1- \frac{p}{100} \right)^n \right\} \times100
$$
と求められます。
パラメーターである$${n, x, p}$$を任意の値に変えることで、任意の確率を求めることができます。現実逃避をしたい方は、試してみてください。
6 おわりに
今まで記事を書いてはきましたが、出るときは10連で出ますし、出ないときは300連回して出ないこともあります。確率はあくまで目安に過ぎません。「5%くらいが当たってラッキー」や、「150連回したけどだいたい50%の確率で出ないから仕方無い」のような心の保養に利用することをおすすめします。自身の天井したガシャの天井確率を求めることは、自身の寿命を短くさせるだけゆえにおすすめしません。以上。ごきげんよう。
7 補遺
察しが良い方はわかったと思いますが、私は野々原茜さんのPちゃんです。

もしもP業に関して私に興味がある方や、記事についての質問は、https://twitter.com/T_notequal_T こちらまで。発現頻度は低いですが、興味がある人など皆無かと思いますので、一応載せておきます。
付録:組合せ・順列・階乗の求め方(高校数学A)
$${_n\text{C}_x}$$の求め方は、
$$
_n\text{C}_x =\frac{n!}{x!(n-x)!}=\frac{_n\text{P}_x}{x!}
$$
であり、$${x=0}$$のとき、組合せは 1通りとします。なお、$${_a\text{P}_b}$$は順列を表し、$${c!}$$は、階乗を表します(なお、$${a, b, c}$$は任意の実数です)。
・順列
$$
_a\text{P}_b=a \times(a-1)\times(a-2)\times\cdots\times(a-b+1)
$$
順列の例
$$
_5\text{P}_3=5 \times 4\times3
$$
$$
_6\text{P}_4=6 \times 5\times4\times3
$$
→$${_a\text{P}_b}$$のとき、$${a}$$からスタートして1ずつ減らしていき、順々に掛けていく。出てくる数字は$${b}$$個
・階乗
$$
c!=_c\text{P}_c=c \times(c-1)\times(c-2)\times\cdots\times2\times1
$$
で表されます。
階乗の例
$$
5!=5\times4\times3\times2\times1
$$
$$
6!=6\times5\times4\times3\times2\times1
$$
→$${c!}$$のとき、$${c}$$からスタートして、1になるまで1ずつ減らしていき、順々に掛けていく。
組合せの例
3回ガシャを引いて目的が0回排出する組合せ
$$
_3\text{C}_0 =1
$$
→排出しない の1通り
3回ガシャを引いて目的が1回排出する組合せ
$$
_3\text{C}_1 =\frac{_3\text{P}_1}{1!}=3
$$
→1回目に排出 or 2回目に排出 or 3回目に排出 の3通り
3回ガシャを引いて目的が2回排出する組合せ
$$
_3\text{C}_2 =\frac{_3\text{P}_2}{2!}=\frac{3\times2}{2\times1}=3
$$
→1, 2回目に排出 or 2, 3回目に排出 or 1, 3回目に排出 の3通り
3回ガシャを引いて目的が3回排出する組合せ
$$
_3\text{C}_3 =\frac{_3\text{P}_3}{3!}=\frac{3!}{3!}=1
$$
→1, 2, 3回目に排出 の1通り
例題の解答
例題の(1)~(4)は、すべて実体験でした。以下、有効数字3桁で解答を示します。
(1) 32.1%

(2) 4.42%

(3) 22.8%

(4) 34.4%
参考
バンダイナムコエンターテインメント. アイドルマスターミリオンライブ!シアターデイズ. https://millionlive-theaterdays.idolmaster-official.jp/ (2023/02/22閲覧)
杉山将. 機械学習のための確率と統計. 講談社, 2013.
