
QuizKnockに教えたい、暗号の解き方解説
先日QuizKnockの動画を拝見しまして、
↓これ
RSA暗号について解説されている良〜い動画でしたね!(偉そうに言ってごめんなさい)
私も一応数学好きなので途中でついつい自分で計算してみたくなり、クイズノックのメンバーが大変な計算で阿鼻叫喚しているところで一時停止してシャーペンを走らせてみました。

メンバーのお二人は途中から電卓を使って計算していましたが、私は手計算で、割と楽に(といっても大変だけど)求められたので、今日はその解法を紹介します。
↓そのときのメモ

要するに、ちょっと自慢したいなという記事です。
決してクイズノックの皆さんに喧嘩を売っているわけではありませんが、より良い方法で解けたら自慢したいじゃないですか!
これでも整数問題には自信があるので、少しだけ偉そうに解説させてください。クイズノック最高です。
動画見てない人はなんのことだかわからないと思いますが、「なんか自慢したいんだね、よしよし」と優しく見守ってくれるか、もしくはそっとページを閉じてくれればありがたいです。
いちおう高校数学レベルなので、整数問題が好きな人はぜひ読んでってくださいな。
合同式がわかる人は読み解けると思います。
〜以下 自分の解法〜
nとdを計算するところは省略します。問題は最後のステップ。
指数がたくさん出てきてパソコンだと打ちづらいので、写真で失礼します。

Mの計算、動画を見る限りクイズノックのお二人はmod2627をそのまま計算していたと思うのですが、これはちょっと効率が悪いと思います。
2627はそもそも2627=37×71と求めた数字なので、せっかくならそれを利用するのが楽です。
mod37とmod71を求めてしまえば、実はここからmod2627を求めるのは結構簡単なんですよねー。高校数学でよく出るアイツを使えばうまくいきます(後述)
(ちなみに「中国剰余定理」という定理が背景にあります、あんまり詳しくは語れませんが)
ということでまずはmod37を求めるわけですが、ここで使えるのがフェルマーの小定理。Youtube内でも別の場面で解説がありました。
フェルマーといえば最終定理ですが、この小定理は割と実用的に(大学入試の難問くらいでは)使えるので、身につけておいて損はないです。大学入試の記述で使うなら証明も書いた方がいいですけどね。

以下、しばらくmod37で話します。
とりあえず指数の319をどうにかもう少し小さな数にしてあげたいですよね。そこで使うのがフェルマーの小定理。これを使うと、
904^36≡1
であることがわかります!嬉しい!(嬉しいんです)
1と合同になる数字がわかると、319を36で割ったあまりを計算すると31なので 904^319≡904^31 であることがわかります。一気に計算が楽になりましたね!嬉しい!
ついでに904≡16なので、あとは16^31を計算すればいいわけです。
この計算なら気合いでいけそうですが、もう一つぜひ使って欲しいテクニックがあります。それが「2乗していけ計算法」です(今命名しました。正式名称あるのかな)
16^31(mod37)の計算は人によっていろいろ工夫はできると思いますが、
この方法ならどんな問題でも、割と簡単な手計算の繰り返しで求められます。

こんな感じで、どんどん2乗を繰り返していくと、
16^1 →16^2 →16^4 →16^8 →16^16 →16^32 →…
というふうに、【(2の累乗)乗】が簡単に計算できます。
16^2などは計算すると≡33になりますが、マイナスで考えることで≡-3になり数字を小さくできます。
実際やってみるとわかりますが、これなら手計算で楽にできるはず!なんなら筆算なしでも頑張れる。今回のmod37なら、適宜マイナスも考えることで18^2より大きな数の2乗は計算しなくていいことになりますからね。便利でしょ?
でもそこからどうすんねんと思ったそこのアナタ。
ここで2進法の知識を使うのです!
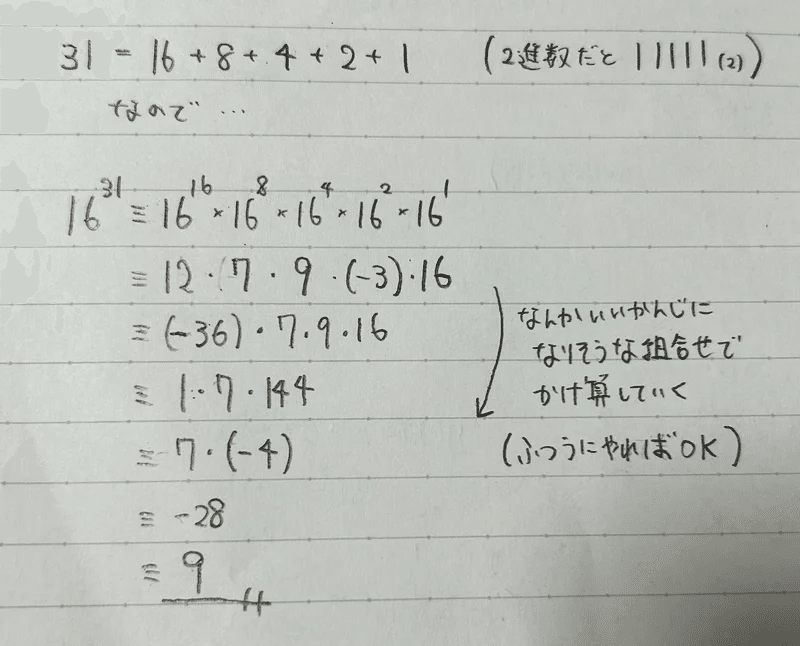
31を2進数表記するときの計算をしてみると(n進数表記をするときに習う特別な筆算を使うなどして求めてね、自分は筆算の仕方は覚えてません)
31= 16+ 8+ 4+ 2+ 1
となるはずです。(31=11111 (2)になる)
これを使って31を分解することで、
16^31≡16^16 ×16^8 ×16^4 ×16^2 ×16^1
と先ほど求めた【(2の累乗)乗】の掛け算で表すことができるのです!指数法則に感謝しましょう。
あとは地道に先頭から掛け算していくもよし(mod37なので18×18より大きな計算はしなくて済みます)カッコつけて工夫するもよし。上の画像では良い掛け算の組み合わせがあったのでカッコつけてます。
計算すれば、16^31≡9 とわかります!!
したがって904^319≡9 つまりa=9です。やったね!ついてこれましたか?
(ちなみに… 逆元の知識があると、16^5 ×k≡1 となるkを求めることで【4k≡-1 → 4k≡36 となり、割と簡単にk=9が出ます】16^31≡16^36×(1/16)^5≡(1/16)^5≡k≡9がわかります)
その次、904^319 (mod71) も同様の流れで計算することができます。
こちらはさっきの37よりは大きいので若干大変ですが、一個一個の掛け算は最大でも35×35程度で済むのでできると思います。君もやってみよう!52^39≡(-19)^39を計算することになると思います。(ここは流れが一緒なので省略)
…ってことで計算できましたかね、bの値を求めると、b=35になります。
これで前半戦は終了です。一旦お疲れ様でした!

ほい、ということで後半戦のスタートです。
まあでも後半戦は完全に高校数学の範囲なので、合同式を知らない人でも解けると思います。そこの君、ペンを取るのである!
いよいよMを求めにかかります。

ここで、904^319について前半戦で分かったことをまとめると、

一気に不定方程式の問題っぽくなったのがわかりますか?
「nは37で割ると9余り、71で割ると35余る。このときnを求めよ」
みたいな問題、見覚えあると思います。
(実際はおそらく「最小の自然数nを求めよ」とかだと思うけど)
今回はとりあえずnを求めちゃうことで自然とMがわかるので、騙されたと思って解いてみましょう。

37k-71L=26
これを解けばいいわけです。
係数が大きいね!!でも手順は一緒なので、手を動かせば解けます。
まずはこの不定方程式の右辺を1にした、
37k-71L=1
これを満たす解をひとつ求める必要がありますね。
てことはアイツの出番です。記事の最初に「(後述)」と書いたアイツです。
みんなで呼びましょう、せーのっ
\ ユークリッドの互除法〜! /
は〜い

てことでk=-23、L=-12が解の一つとして求まります。
これができたらもうこっちの勝ちですね。解くところまで一気に行っちゃいましょう。
今求めたのは37k-71L=1の解なので、=26の解を出すために26倍することに注意です。

はい、これで k=71m-598, L=37m-312(mは整数)が無事に求まりました!これを最初のnの式に代入すると…!

掛け算が少し面倒ですが、そこを乗り越えれば
n=2627m-22117 が得られます。
…ってことは、この式をよく見れば、
「nを2627で割った余りは、-22117を2627で割った余りに等しい」ことが、
つまりn≡-22117 (mod2627)がわかります。
(最後だけ合同式の知識が必要でしたね、すみません)
マイナスがついていると嫌なので一旦計算が簡単なので+26270をして、あとはちょちょいとやれば…
n≡1526 (mod2627)
したがって
M=1526
が求められました!!
やったね!おめでとう!これで暗号が解読できます。お疲れ様でした!!
…いかがでしたでしょうか。これでアナタも暗号解読者ですね、おめでとう!
クイズノックにスカウトされたりしないかな、、ないか。整数担当の枠が空いてたら呼んでください。
え、ふくらPには敵わないから無理?…ですよね、すみませんでした。精進します。
ま、結構ちゃんと解説ができたんじゃないかな〜と自分的には満足です。
「よくわからんけど難しいこと書いてあるな」と思っただけだとしても、自慢したいという当初の目的は達成されたのでOKなのだ!笑
ためになった人はぜひクイズノックの動画の方の高評価を押しといてください。以上、すりーむーんでした。
この記事が気に入ったらサポートをしてみませんか?
