3次元極座標と図形の方程式

動機

2次元極座標平面$${(r,\theta)}$$では、方程式

$$
\begin{align*}
r&=\theta\\
r&=1\\
\theta&=\dfrac{\pi}{4}
\end{align*}
$$

が表す図形が、それぞれ螺旋や円や直線になることを勉強しました。高校数学の数IIIでやると思います。(今は数学C？)

では、3次元極座標空間$${(r,\theta,\phi)}$$において、

$$
\begin{align*}
r&=\theta\\
\theta&=\phi\\
\phi&=r
\end{align*}
$$

や

$$
\begin{align*}
r&=\text{const.}\\
\theta&=\text{const.}\\
\phi&=\text{const.}
\end{align*}
$$

はどのような図形を表しているのでしょうか？

極座標と直交座標の相互変換

$${x,y,z}$$と$${r,\theta,\phi}$$の関係式を示します。

$$
\begin{cases}
x=r\sin\theta\cos\phi\\
y=r\sin\theta\sin\phi\\
z=r\cos\theta\\
\end{cases}
\,\,\,
\left(r\geq 0,
0\leq\theta\leq\pi,
0\leq\phi<2\pi\right)
$$

$$
\begin{cases}
r=\sqrt{x^2+y^2+z^2}\\
\theta=\arccos\dfrac{z}{\sqrt{x^2+y^2+z^2}}\\
\phi=\text{sgn}(y)\arccos\dfrac{x}{\sqrt{x^2+y^2}}
\end{cases}
$$

直交座標では(復習)

1変数＝定数

$${x=1,y=1,z=1}$$などの、「1変数＝定数」は、それぞれ$${yz,zx,xy}$$平面を、$${x,y,z}$$方向に定数分だけ平行移動した平面になります。

1変数＝1変数

$${x=y,y=z,z=x}$$などの、「1変数＝1変数」は、直線$${x=y,y=z,z=x}$$をそれぞれ$${z,x,y}$$方向に平行移動して通過した部分からなる平面になります。

極座標では

では極座標について考えます。形がイメージにしくいものは、グラフ描画のソフトを使って描いてみます。

r＝定数

$${r=1}$$を考えます。これは半径1の球になります。2次元の場合は半径1の円になるので、予想通りというかイメージしやすいです。

θ＝定数

$${\theta=\dfrac{\pi}{4}}$$を考えてみます。これは、円錐面になります。

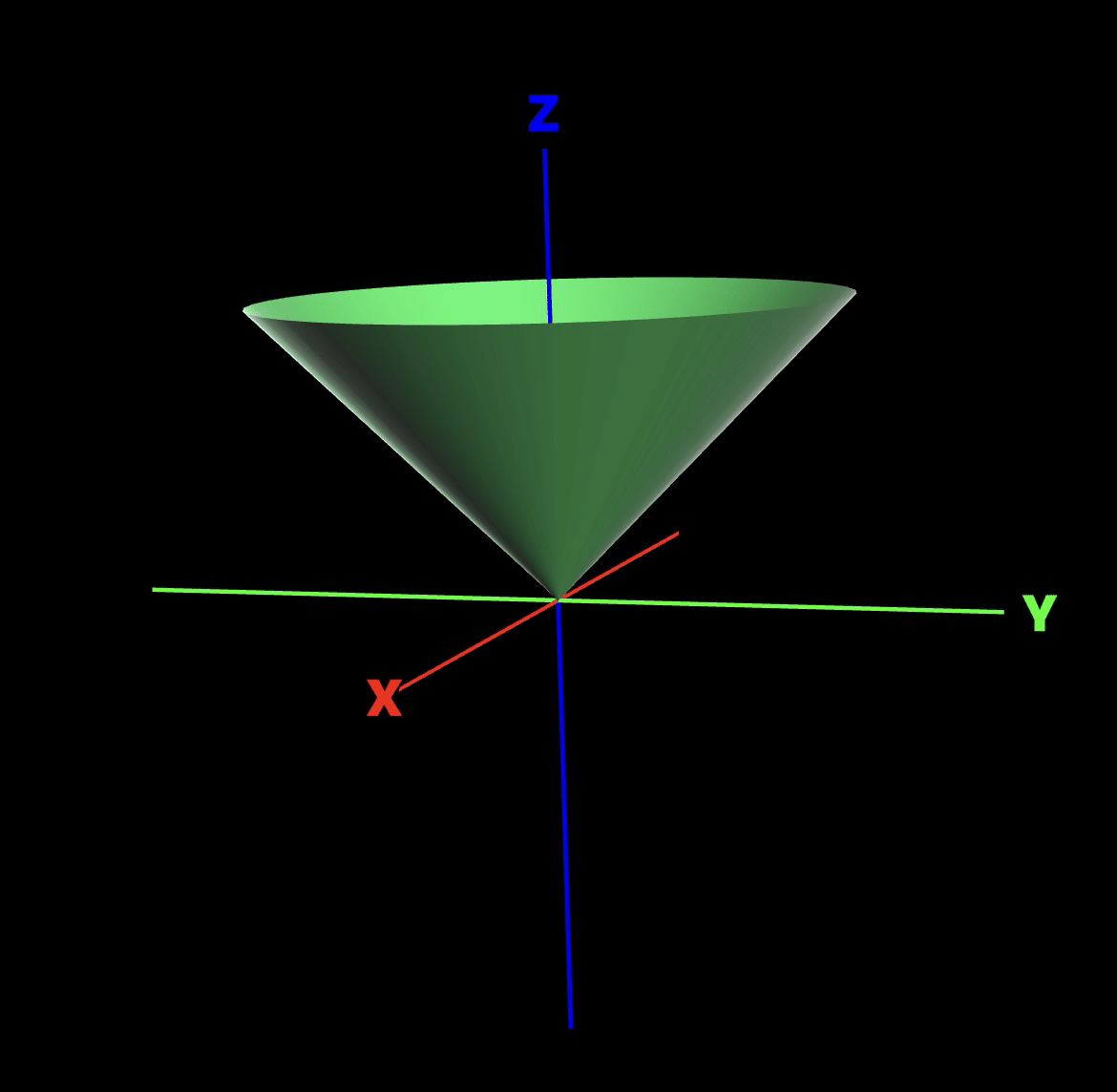
$${x,y}$$平面上の原点に立って、空を見上げる角度を常に$${\dfrac{\pi}{4}}$$に保ちながら、その場でぐるりと1回転したというイメージでしょうか。

φ＝定数

$${\phi=\dfrac{\pi}{4}}$$を考えてみます。
これは、図のような平面(半径無限大の半円板)になります。

イメージとしては、$${xy}$$平面上の原点に立って、ある$${\phi}$$方向を向いて天井から地下まで視線を動かしている感じでしょうか。

r＝θ

$${r=\theta}$$はこんな感じ。

色合いも相まって、梨みたいですね(美味しそう)

下からの視点

縦にスパッと切れば、2次元極座標の$${r=\theta}$$の形が出てくるっぽい感じがします。

θ＝φ

$${\theta=\phi}$$はこんな感じ。

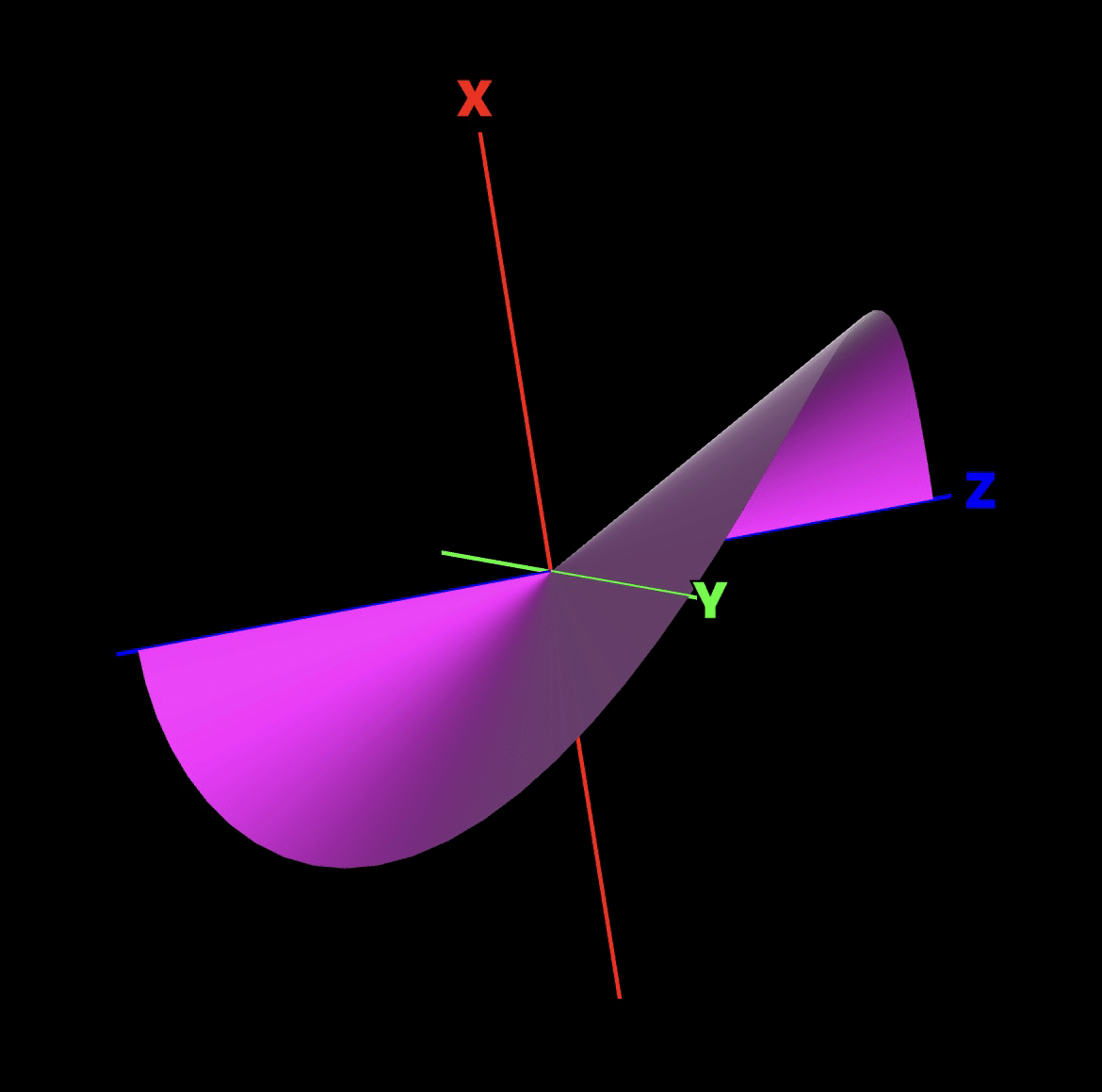
なんかロゴマークとかでありそう。

φ＝r

$${\phi=r}$$はこんな感じ。

貝殻みたい。

以上です。ありがとうございました。