ABC172振り返り
かなり久しぶりになってしまいましたが、ABC172の振り返りをします。
最近環境が変わりしばらくコンテスト自体にも出られていなかったのですが、ぼちぼちAtCoderも再開しようと考えています。
ABC172の結果は26分A-D4完でレートがそこそこ上がりました。
D問題まではスムーズに解けていると言っていいと思います。
EのNEQ、FのUnfair Nimは半年ほどたった今でも印象に残っています。
A問題
値を出力します。
int main(){
ll a; cin >> a;
cout << a + a * a + a * a * a << endl;
}B問題
S,Tの文字列の長さが同じで、その長さが2*10^5以下なので一文字ずつ見ていけば良いです。
int main(){
string s; cin >> s;
string t; cin >> t;
ll n = s.size();
ll ans = 0;
rep(i,n){
if(s[i] != t[i]){
ans++;
}
}
cout << ans << endl;
}
C問題
想定よりdifficultyが高かったですがここはすんなり解法が思い浮かびました。
机Aの読む本を固定した時に、机Bを何冊読むかを求めます。
A, Bの累積和を事前にとっておくことで何冊読むのに何分かかるかのベクトルを生成します。
また、正の数の累積和なので単調増加になります。
よってその後二分探索でそれぞれの机Aの読書数に対して、机Bから何冊まで読む時間があるかO(logN)で求められます。
int main(){
ll N , M , K; cin >> N >> M >> K;
vector<ll> a(N); rep(i,N) cin >> a[i];
vector<ll> b(M); rep(i,M) cin >> b[i];
vector<ll> asum(N + 1);
vector<ll> bsum(M + 1);
rep(i,N){
asum[i + 1] += asum[i] + a[i];
}
rep(i,M){
bsum[i + 1] += bsum[i] + b[i];
}
ll ans = 0;
rep(i,N + 1){
ll tmp = 0;
if(asum[i] > K) break;
else{
tmp = i;
tmp += POSU(bsum , K - asum[i]) - 1;
ans = max(tmp , ans);
}
}
cout << ans << endl;
}D問題
この問題も問題を読んでまずエラトステネスの篩が思い浮かびました。
エラトステネスの篩の事前処理の計算量がO(N loglogN)です。
それぞれの正整数の処理が間に合うかどうかは素数である約数の個数についての見積もりが大事ですが、10^7までの正整数に対する素数約数の個数は最大10程度で平均は5程度ではないかと考えました。
この問題では N = 10^7だったので通るか微妙だなと感じたのですがコードテストで10^7の入力に対して時間内で実行されたので提出したところACになりました。
struct Sieve {
ll n;
vector<ll> f, primes;
Sieve(ll n=1):n(n), f(n+1) {
f[0] = f[1] = -1;
//エラトステネスの篩
for (ll i = 2; i <= n; ++i) {
if (f[i]) continue;
primes.push_back(i);
f[i] = i;
for (ll j = i*i; j <= n; j += i) {
//最小素因数がかかれるようにしている
if (!f[j]) f[j] = i;
}
}
}
bool isPrime(ll x) { return f[x] == x;}
//素因数列挙
vector<ll> factorList(ll x) {
vector<ll> res;
while (x != 1) {
res.push_back(f[x]);
x /= f[x];
}
return res;
}
//頻度を集計したもの
vector<P> factor(ll x) {
vector<ll> fl = factorList(x);
if (fl.size() == 0) return {};
vector<P> res(1, P(fl[0], 0));
for (ll p : fl) {
//小さい順に出てくるので前回と同じなら足す作業でmapが作れる
if (res.back().first == p) {
res.back().second++;
} else {
res.emplace_back(p, 1);
}
}
return res;
}
};
int main(){
Sieve sieve(1e7 + 10);
ll N; cin >> N;
ll ans = 0;
repn(i,N){
vector<P> a = sieve.factor(i);
ll tmp = 1;
rep(j , a.size()){
tmp *= a[j].sc + 1;
}
ans += tmp * i;
}
cout << ans << endl;
}実際に素数の約数の個数について調べてみました。
N = 10^6の時1-Nまで、素数約数の個数は平均2.85371
N = 10^7の時1-Nまで、素数約数の個数は平均3.01303でした。
想定よりも少なかったです。エラトステネスの篩の方が計算量多かったみたいです。
ここら辺の知見あったらぜひ教えて欲しいです。
解説の解法は賢いと感じました。
それぞれの正整数ごとに約数になる時を足していくという発想でした。
ll fac(ll n){
return n * (n + 1) / 2;
}
int main(){
ll N; cin >> N;
ll ans = 0;
repn(i,N){
ans += i * fac(N / i);
}
cout << ans << endl;
}E問題
実際に手を動かしていていて完全順列がらみの問題だなと感じていましたが、解けませんでした。
包除原理の考え方を利用することで理解できました。
以下サイトが参考になりました。
蟻本264ページの内容も勉強になりました。
自分は最初解法をみてもわかりませんでした。
イメージとしては、いきなり問題の二つの条件を満たす数列の個数を求めることは難しいので、計算しやすいところから包除原理を利用して条件を満たす数列の個数を求めるといった解法です。
以下解答のそれぞれの項が何を計算しているのか(解答参照)
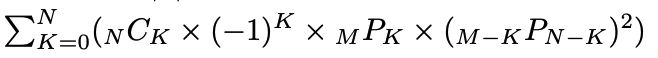
これのKはAとBに確定で何文字AとBにA_i = B_iを満たす箇所があるか
第一項はその箇所の選び方
第二項(-1)^kは包除
第三項は確定で同じ部分の選び方(順列)
第四項はA,Bの確定部分以外の順列
注意なのはもちろん第四項の部分でさらに条件を満たす部分が出てくるかもしれない点です。
int main() {
// 前処理
COMinit();
ll N , M; cin >> N >> M;
ll ans = 0;
for(ll i = 0; i <= N; i+= 2){
ans += COM(N , i) * fac[M] % MOD * finv[M - i] % MOD
* fac[M - i] % MOD * fac[M - i] % MOD
* finv[M - N] % MOD * finv[M - N] % MOD;
ans %= MOD;
}
for(ll i = 1; i <= N; i+= 2){
ans -= COM(N , i) * fac[M] % MOD * finv[M - i] % MOD
* fac[M - i] % MOD * fac[M - i] % MOD
* finv[M - N] % MOD * finv[M - N] % MOD;
ans += MOD;
ans %= MOD;
}
ans %= MOD;
cout << ans << endl;
}
なかなか文章で包除原理を伝えるのが難しく、わかりにくいかもしれません。
F問題
Nimの必勝法については軽く学んだことがあったのでできるかもと思いましたが、Nimは知っている前提の問題だったようでできませんでした。
この問題の復習にあたり蟻本4-2「ゲームの必勝法を編み出せ!」を読みました。
他の章との関連はそこまでないので飛ばしてここだけ読むのも勉強になると思います。(特にゲームが好きな方は入りやすいと思います。)
Grundy数については初めて知りました。理解するのに時間がかかりましたが、面白い概念だと感じました。
解説がわかりやすいですが理解に時間がかかったので、備忘録として自分のイメージを書いてみます。
今回の問題では、最初の二つの和(Sとする)を保ちながら最初の二つのxorをその他のxor(Xとする)と一致させたいです。
D = (S - X) / 2を考えます。
最初の二つの数字それぞれがDをもち、xorでなくすイメージです。
そのDの他に消せるものを消した後の残りの値が答えです。
わかりにくいので具体例です。
例えば、N = 8, A = (10, 9, 8, 7, 6, 5, 4, 3)の時
S = 19, X = 11になります。
この時 D = (S - X) / 2 = 4です。
10から2^2は必須で保有するので、残り6を超えないように最大限2^xを引いていきます。
今回の場合は2^1, 2^0は引くことができるので6 - 2^1 - 2^0 = 3が答えです。
2 ^ 2は必要なので消せない、残り0b1011から最大6まで消せるけどいくつ消せるという問題です。
int main(){
ll N; cin >> N;
vector<ll> a(N); rep(i,N) cin >> a[i];
ll s = 0, x = 0;
s = a[0] + a[1];
for(ll i = 2; i < N; i++){
x ^= a[i];
}
ll d = s - x;
if(d < 0 or d % 2 == 1) cout << -1 << endl;
else{
d /= 2;
// 関係ないところで消さなきゃいけない
if((d & x) != 0) cout << -1 << endl;
else{
bitset<50> bs(x);
// maxの値はxの中からa[0] - dの値
ll ans = a[0] - d;
for(ll i = 49 ; i >= 0; i--){
if(bs.test(i) and ans > modpow(2, i)){
ans -= modpow(2, i);
}
}
if(ans == a[0] or ans < 0) cout << -1 << endl;
else cout << ans << endl;
}
}
}めっちゃわかりにくいかもですが書きました。
何かコメントなどあれば気軽にお願いします。
よろしければ少額でもサポートお願いします。サポートの費用対効果は抜群です。
