除法の筆算の土台　｜基礎計算研究所

÷１桁と÷複数桁の共通点、そして大きな相違点

　乗法の際，複数桁×複数桁は、乗数の桁数分の「複数桁×1桁分」の計算が構成要素になっている。

　しかし÷複数桁の除法の筆算においては，÷１桁の筆算はその構成要素にはなっていない。ここが様相が異なるので注意が必要である。

　具体的に言うと，483×72を筆算するときは、483×7と483×2に分解して計算を進めるが、3674÷73の筆算は3674÷7と3674÷3に分解して計算するわけではないのである。

　乗法では九九（素過程）を組み合わせてまず×１桁をつくり、それを部品に×複数桁を構成するという2段構えであった。ところが、除法の場合は÷１桁は÷複数桁の構成要素とはならないのである。

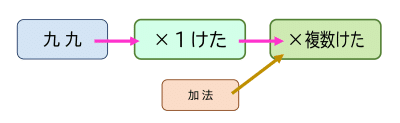
筆算における「加減乗・÷１桁の除法」と「÷複数桁の除法」の大きな違い

　では、÷１桁と÷複数桁とでは、何が異なるのであろうか。それは加減乗算と÷１桁の筆算は素課程によって確定した数値をすぐに紙の上に書いていく過程である。間違いがなければ、書き直しはない。ところが、÷複数桁の筆算は「仮商（かりの商）」を立てるところからスタートし、商（真商）を探り当てる、という試行錯誤の過程が避けられない。

　もちろん÷１桁でも試行錯誤の過程は存在する。しかし、それは九九を何回か暗唱することによって解決しているのである。複数桁×１桁ではそうはいかない。実際にかけ算（筆算！）をするしかないのである。

　現在、÷１桁を短除法で扱っている教科書はない。水道方式では「同じ形式・同じ手続きで計算ができる」と、÷１桁も÷複数桁も長除法で解く、と言うことを提唱し，その後、東京書籍も啓林館も短除法を扱わなくなった。（なお、公文式は短除法である）

cf. 長除法と短除法

　÷複数桁の筆算は、ここまでの筆算の体系になかった仮商をたてるという試行錯誤のアルゴリズムが存在している。紙に書きつけた数字が正解とは限らないという仮商の試行錯誤は、ほかの筆算にない特異なプロセスである。

　これが乗法のときになかった複雑化である。÷複数桁は÷１桁の単純な合成ではない。

　÷１桁から÷複数桁を「おなじ書き方」で揃えたことである。つまり，「たてる」→「かける」→「ひく」→「おろす」のアルゴリズムと、その表記法をそろえた、というである。しかし，残念ながら、「加減乗と÷１桁の除法まで」と「÷複数桁」には、紙に書きつけた数字が最終的に残らないかもしれないという、仮商・試行錯誤へのジャンプが存在し、そのことが筆算の研究としては課題となるのである。

　÷１桁の計算は、筆算のアルゴリズムや表記形式が同じでも、÷複数桁の部品としては使えないのである。

　そして、これは最近の教科書に掲載されているように，世界での除法の筆算の形式は統一されたものがなく、この２００年程度の初等教育の定着の中で、それぞれの地域で定着し標準化されたものが，それぞれの地域で定着している，というもののようである。そもそも除法記号"÷”を使うのも、世界から見ると少数派である。

　話が脱線しそうになったが、「÷複数桁」の部品として「÷１桁」が使えない、ということを確認したかったのである。ここで、「÷複数桁」の手前にある「÷１桁」についての考えとしては２つある。アルゴリズムと表記形式を統一するという方式で行くか、アルゴリズムも別物であるので形式も別物と考えるか，ということである。

　加えて、この仮商の立て方には、4つの流儀があり、教科書によっても全て紹介しているものから、１つの流儀のみに絞っているものがある。

　とかく教科書通りを求められる日本の教育では，教科書通りに事を進めた方がいいのも確かであるが、思いとしては、×複数桁のときにも述べたように、あまり÷複数桁を正確に計算することを追求しすぎず、ざっくりアルゴリズムを押さえた上で、なぜその方法で計算ができるか、考える・伝え合う、ということの方を重視する方がいいのではないか，と思う。もちろん、わり算を使うことで何を求めることができるのか、などなど、計算技術の習得よりも、これから求められるのはそちらの方である。実際の計算は，もうこの時代、人間を機械化するのではなく、この部分は電卓だのスマホだの科学技術に頼ればいいのではないか、と思う。（そういう点では、円周率をおよそ３として，ざっくり計算する「ずるさ」を身につける、×３．１４なんて電卓でちゃちゃっと計算してしまった方がよいことも，数処理の知恵として覚えたらよいのでは、と思う。もうすでに一人１台なんらかの端末を手にしながら学習をする時代なのだし。ゆとり教育の象徴として批判されたアレは、ちょっと時代が早すぎたのか・・・　）

　話がズレた。とりあえず，ここで言いたいのは、÷複数桁の分析は，÷１桁の分析を単純に組み合わせたものとはならず、様相が異なるものになる、ということである。これ以上詳しくは÷複数桁のところでまた詳しく解説することにして，まずは÷１桁の計算について，述べていくことにしよう。