
約分:最大公約数でわる・・・? |基礎計算研究所
教科書には、約分するときには分子と分母の最大公約数を見つけて、それで割ると1回で約分ができる、ということが書いてあります。

(2021年度版5年生各社算数教科書より)
しかし、最大公約数を見つけるのが一番いいわけではありません。
ここでおすすめするのはできるだけ大きな1桁の公約数を見つける(ダメなときもあるけど)、ということです。(最大公約数、と書いていない教科書は、その当たりわきまえているからでしょうか?)
同じわり算でも、÷1桁の計算と÷2桁の計算では,面倒さが相当ちがいます。できるだけ÷1桁の計算で済ますことができれば、それに越したことはありません。わり算のむずかしさとして、
÷1桁=1桁(九九1回で済むわり算) << ÷1桁=複数桁 << ÷複数桁
のようにわり算の面倒さがそれぞれに各段にちがうのです。÷18をするときに、÷2をした後÷9をしたり、÷6をした後÷3をしたりした方が,÷18を筆算でやろうとするよりも実は早いのです。
教科書では、さも「1回で約分が済む」ということが最速最短の方法のように見えています。しかし、そこに至るまでの計算の負荷や総量については全く触れていません。そして、どの教科書も最大公約数が1桁の場合のみ例を取り上げています。例えば36/54の約分はどうでしょう。最大公約数は18です。計算の負荷や総量に注目して、都合の良い例だけではなく、いくつかの場合をみていくことにしましょう。その上で、なぜ「できるだけ大きな一桁の公約数で数回」が「最大公約数で1回」よりも良い戦略と言えるのか、検討していきます。
最大公約数を見つけるだけで大変では・・・?
たとえば36/54を約分することを考えます。最大公約数は18です。
最大公約数を見つけるにはどうしましょう。いくつか方法がありますが、まずは教科書で約分の直前ぐらいに出てくる方法を確認しておきます。
(その1)2つの数の約数をそれぞれ書いて、その中から同じ数を見つける
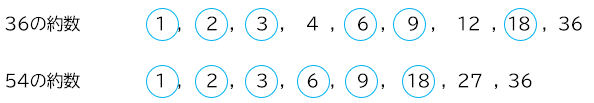
(その2)小さい方の約数の中から、大きい方の約数を見つける
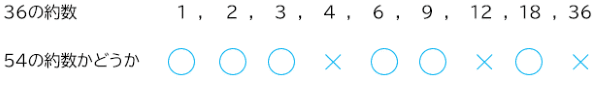
このように、教科書の図だけ見ると、さらりと約数が並んで、さらりと比較ができて、やっているように感じるかも知れないけれども、実際どういう計算をしているか、ということを一つ一つ見てみると
★2つの数の約数をそれぞれ書いて、その中から同じ数を見つける
約数を見つけるときに、九九1回のわり算ではない36÷2=18、36÷3、54÷2、54÷3、54÷4、54÷5が必要です。
★小さい方の約数の中から、大きい方の約数を見つける
54÷2,54÷3,54÷4,54÷6,54÷12,54÷18,54÷36と、実は面倒なわり算の計算が多く出てくるわけです。
最大公約数だけ見つければいいので、36の約数の大きい方から確かめてみるにしても、54÷36、54÷18という、÷2桁の計算をしなければならないのは変わりません。
÷2桁の計算は大変!
さて、最大公約数が18と出てきたので、今度は18で分子と分母をわってみると、36÷18=2,54÷18=3で、2/3と約分が1回で済みます。しかし、2桁÷2桁の計算は筆算を持ち出さないといけないので、約分の回数を減らすメリット以上に計算が面倒になります。54は9×6なので、36が9や6でわれるかどうか、を考える方が計算が簡単です。
2回約分が必要になりますが、九九の範囲であれば基本は筆算のいらないわり算だけで済みますし、九九の範囲を超えて筆算が必要になっても÷2桁よりも÷1桁は結局九九適用のわり算を繰り返すだけですので、÷2桁の筆算よりも格段に楽です。
そして、ここで最大公約数は18とさらっと言いましたが、最大公約数が18である、ということを求めるためにも上のように計算が必要です。
教科書には「最大公約数をまず見つけて、それでわる」ということが書いてありますが、それは約分を1回で済ますのがよい、という発想であり、そのための細かい計算の量は考慮をされていません。
九九を利用することができれば、できるだけ大きな1桁の公約数を見つけることも可能なので、(何回かかかるかもしれないけど)わる、という方が、計算の素早さはちがいます。

「できるだけ大きな1桁の公約数」はどうやって見つける?
しかしそうは言っても、約分回数を少なくすることは計算の総量を減らすためには外せないポイントです。そのために「できるだけ大きな1桁の公約数」としているのです。では、その「できるだけ大きな1桁の公約数」とやらは、どのように見つければよいのでしょう。
約分の練習をするときに、あまりどこにもはっきりと書いていないけど、多くの人が利用しているルールがあります。それが「九九の活用」です。分子と分母が九九の同じ段にあるかどうかを考えてみることです。先ほどの36/54の例を考えてみましょう。まず同じ偶数どうしなので2でわって18/27、3でわって6/9、さらに3でわって2/3、これ以上公約数がないので既約、としてもいいのでが、54は=6×9で、36も6の段や9の段にある数なので、6でも9でもわり切れます。「できるだけ大きな1桁の公約数」のルールで行くと、9で分子・分母をわると4/6。このわり算は「九九を利用するわり算」で簡単にできます。それで、さらに2で約分ができて、2/3で既約ですね。
「九九を活用する」というやり方は、なかなか文字として示しているものが見当たりません。(得意な人がなんとなくやっている、という暗黙知の領域に入るものなのでしょうか)。
九九分解で見つけるコツ
できれば、分子・分母のうち大きい方の数をまずは九九で分解できるかを考える、というのがいいかもしれません。小さい数だと、例えば36は4*9と6*6の2通りに分解できて、幾つもの組合せの中から考える必要があります。数が大きくなればなるほど、九九で分解できても1通りしかない可能性が高くなります。
(ちなみに2通りに分解できる九九は12=2*6=3*4、16=2*8=4*4、18=2*9=3*6、24=3*8=4*6、36=4*9=6*6)
九九で分解できなければ、次の手、とすればよいのです。
この記事が気に入ったらサポートをしてみませんか?
