書記が数学やるだけ#112 フーリエ級数の一般化， パーセヴァルの等式

今回はフーリエ級数の一般化について見ていく。また，パーセヴァルの等式の応用についてもここで扱う。

問題

説明

[0,π]で定義された関数を周期関数へと拡張するのに，偶拡張と奇拡張がある。

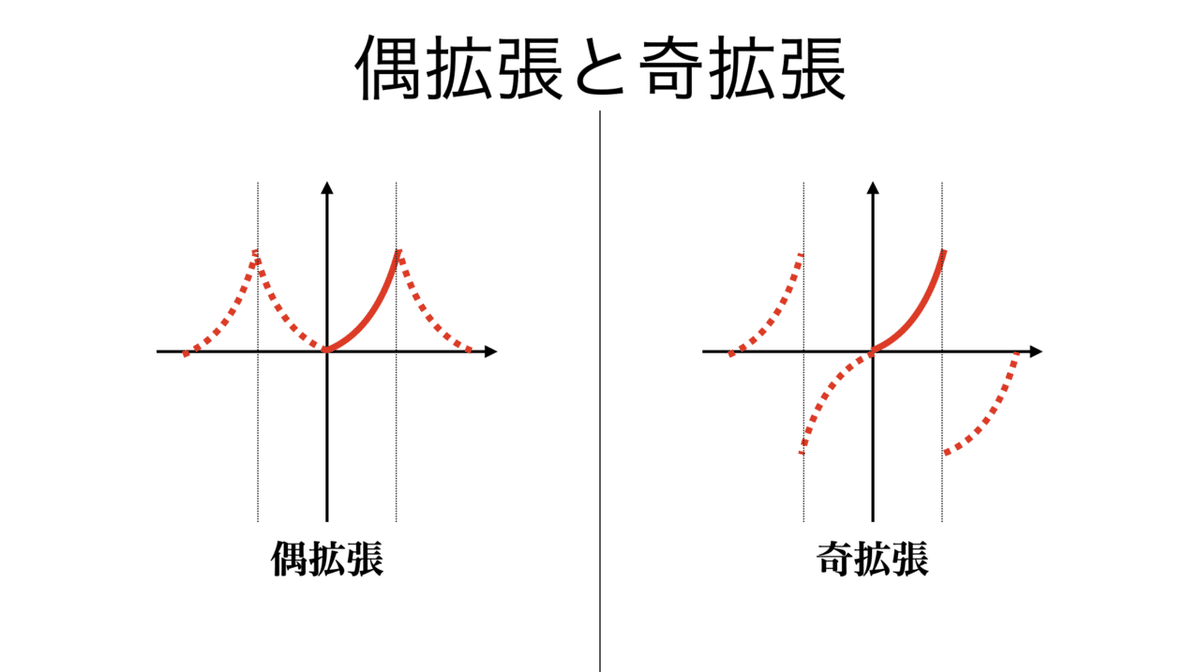
それぞれの片割れに対して，フーリエ余弦級数とフーリエ正弦級数が定義される。

さて，今までのフーリエ級数は周期2πであったが，変数変換をすることで一般の周期に拡張できる。

更にフーリエ級数は複素数に拡張できる。方法としてはオイラーの公式を用いる。

最後に，パーセヴァルの等式とそれに関連する定理についてのメモ。

解法

フーリエ正弦関数，フーリエ余弦関数の導出は，フーリエ級数と同じような計算でできる。

フーリエ級数とパーセヴァルの等式を組み合わせることで，特定の無限級数和を求めることができる。

本記事のもくじはこちら：