
書記が数学やるだけ#764 2次不定方程式の整数解
2次不定方程式の整数解について,入試問題を例に見ていく。
問題

説明
2次不定方程式の整数解は,判別式により性質が大きく異なる。詳しいことは代数幾何学を扱う際に見ることとする。

解答
2次不定方程式の問題は因数分解できさえすれば簡単なのだが,流石に東大ではそうはいかない。本問では逆像法を用いて解の範囲を絞るのが良いだろう。x,yともに有限の範囲で,整数解(0,0)があることから,有限個の整数解を持つことが示される。

次に千葉大の問題について,まずは誘導に従ってみる。
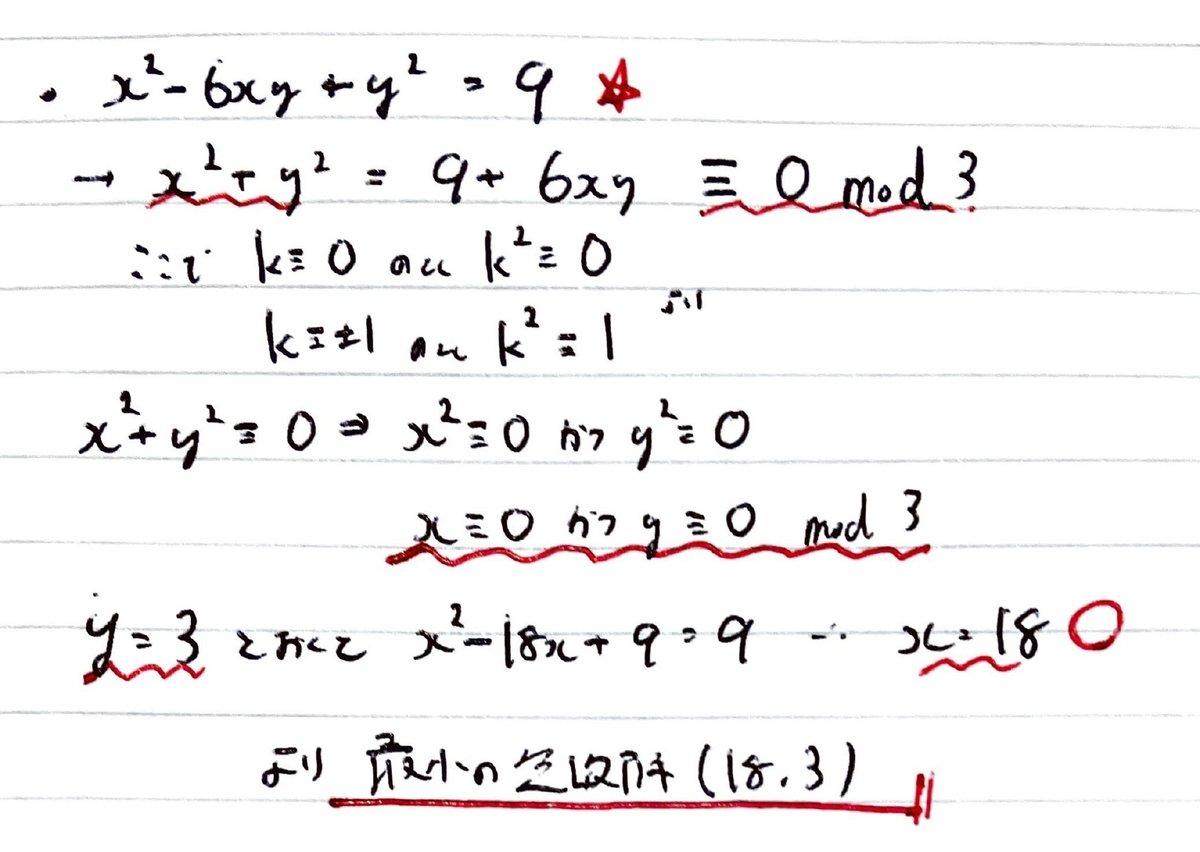

無数個の解を持つことは,一つ整数解があればある増加数列の漸化式に沿って整数解を生成できることによる。以前に解いたお茶の水大の問題の応用である。

本記事のもくじはこちら:
学習に必要な本を買います。一覧→ https://www.amazon.co.jp/hz/wishlist/ls/1XI8RCAQIKR94?ref_=wl_share
