書記が数学やるだけ#784 ベイズ統計におけるモデル選択

ベイズ統計におけるモデル選択の方法をいくつか見ていく。

問題

説明

回帰分析における変数選択について，特にAICを見てきた：

そのほかにも以下のような基準があり，PyMC3で計算することができる。

別の基準として，事後確率の比であるベイズファクターが用いられている。

解答

事前分布は以下の形をしており，確率0.3というのであればB(4,8)の方が近いように見える。

ベイズファクターのモデルを作成する。

coins = 10
heads = 3
y_d = np.repeat([0, 1], [coins-heads, heads])

with pm.Model() as model_BF:
    p = np.array([0.5, 0.5])
    model_index = pm.Categorical('model_index', p=p)
    m_0 = (4, 8)
    m_1 = (8, 4)
    m = pm.math.switch(pm.math.eq(model_index, 0), m_0, m_1)
    theta = pm.Beta('theta', m[0], m[1]) y = pm.Bernoulli('y', theta, observed=y_d)
    trace = pm.sample(5000)

pm.traceplot(trace)
plt.figure()

pM1 = trace['model_index'].mean()
pM0 = 1 - pM1
BF = (pM0/pM1)*(p[1]/p[0])
print(pM0, pM1, BF)
#出力　0.8206 0.1794 4.574136008918617

これによりベイズファクターは4.57と算出され，これはB(4,8)の方が十分に望ましいことを示している（基準についてはRaftery(1995)など参照）。

次にWAICとLOOを算出する，これには個別にモデルを組み立てる必要がある。

with pm.Model() as model_BF_0:
    theta = pm.Beta('theta', 4, 8)
    y = pm.Bernoulli('y', theta, observed=y_d)
    trace_0 = pm.sample(5000)  

pm.traceplot(trace_0)
plt.figure()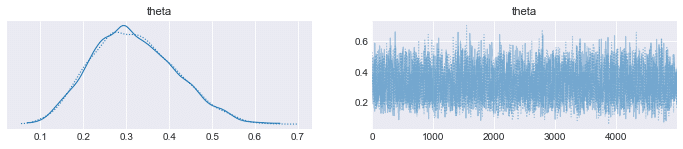

with pm.Model() as model_BF_1:
    theta = pm.Beta('theta', 8, 4)
    y = pm.Bernoulli('y', theta, observed=y_d)
    trace_1 = pm.sample(5000)

pm.traceplot(trace_1)
plt.figure()

まずはWAICの計算から，これによりB(4,8)の方が優れていることがわかる。

import arviz as az
df_comp_waic = az.compare({"BF_0": trace_0, "BF_1": trace_1}, ic="waic")
az.plot_compare(df_comp_waic, insample_dev=False);

LOOについても同様の結果であった。

df_comp_loo = az.compare({"BF_0": trace_0, "BF_1": trace_1})
az.plot_compare(df_comp_loo, insample_dev=False);

では，1000回投げて300回表が出た場合ではどうなるか。表が出た確率は同じだが試行回数が多い分確信度が高いようにも思える。

ベイズファクターについては以下の通りで，B(4,8)の方が一層望ましいことを示している。

#出力0.9618 0.0382 25.17801047120419

一方でWAIC・LOOを比較すると，両モデルの良し悪しの差はほとんどないことが示される（図はLOO）。

この違いを考えるために，事後分布のグラフを見てみる。

10回投げた場合は，B(4,8)の方が表の確率0.3であることをよく示せている。

一方で1000回投げると，両モデルで事後分布に差が見られないことがわかる。

このことから，WAICやLOOといった指標は事後分布の影響を受けやすく，一方でベイズファクターは事前分布の影響を受けやすいことが考えられる。

本記事のもくじはこちら：