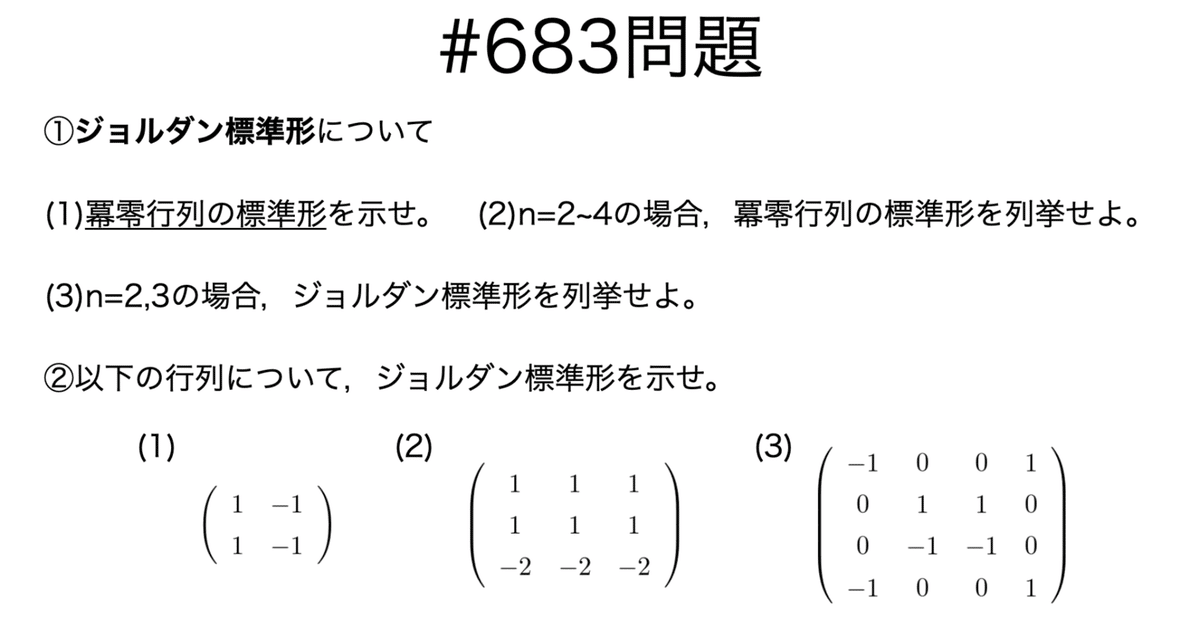
書記が数学やるだけ#683 ジョルダン標準形の導出
前回示したジョルダン分解より,冪零行列のジョルダン標準形が示せればよいことがわかる。
問題
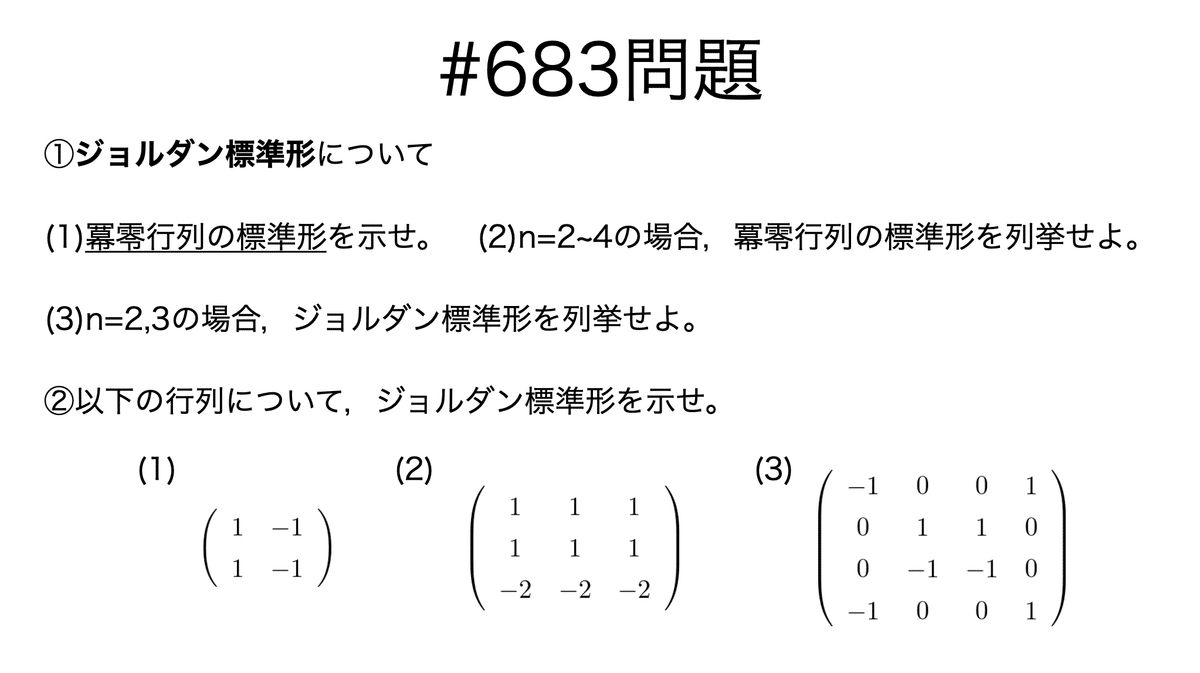
説明
任意の正方行列は,ジョルダン細胞を用いた分解で表すことができる(ジョルダン標準形)。
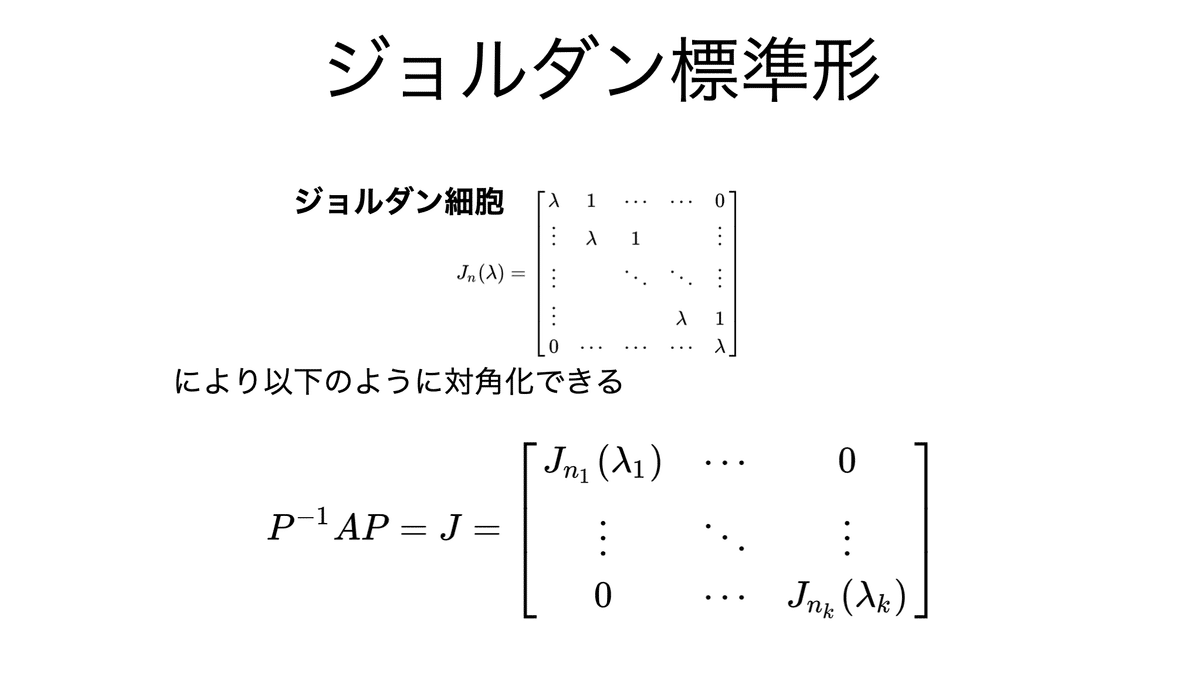
一般の場合では,以下のようにアルゴリズム的に求めることになる。

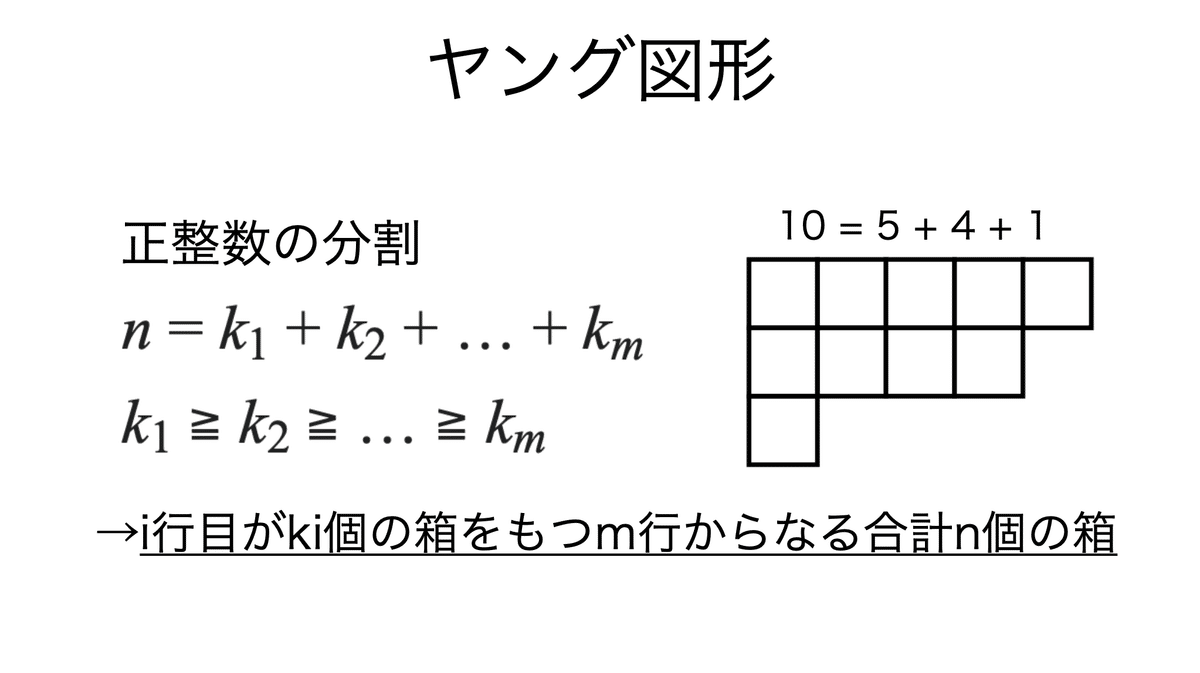
ヤング図形は表現論において重要である。ここでは基底を考える上でヤング図形が出てくることだけに説明をとどめておく。
解答
冪零行列を分解するために,以下のような減少列から基底を作っていく。


冪零行列のジョルダン標準形について,いくつか具体例を示しておく。

一般の行列のジョルダン標準形について,n=2,3では固有多項式と最小多項式のみから一意に決まる。


具体例をいくつか。手順としては,まず最小多項式からジョルダン標準形を決め,条件を満たすような基底を決め,最終的に対角化できることを確かめる。

基底を決めるために,ヤング図形に基づくダイアグラムが有効である。

n=4以上の場合は最小多項式のみではジョルダン標準形が決まらず,基底の線形独立性を確かめていく必要がある。

本記事のもくじはこちら:

