書記が数学やるだけ#641 分割法，測定の繰り返し

実際の測定では順番を完全にランダムにするのは効率的ではなく，分割法が行われることが多い。

問題

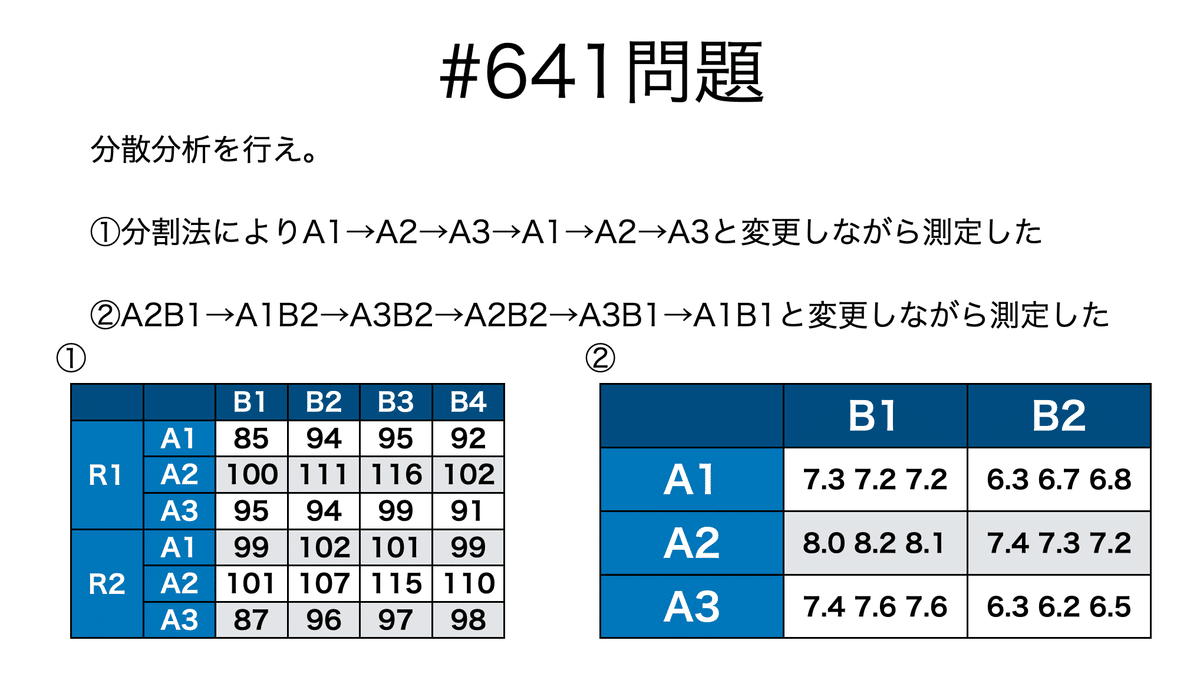
説明

例えば，500℃から700℃の温度槽を扱う際に，毎回ランダムに温度変更をするのは容易でないことがある。その際には，分割法により温度を固定して他要因を変更して測定するという方法により，温度変更を大幅に削減できる。

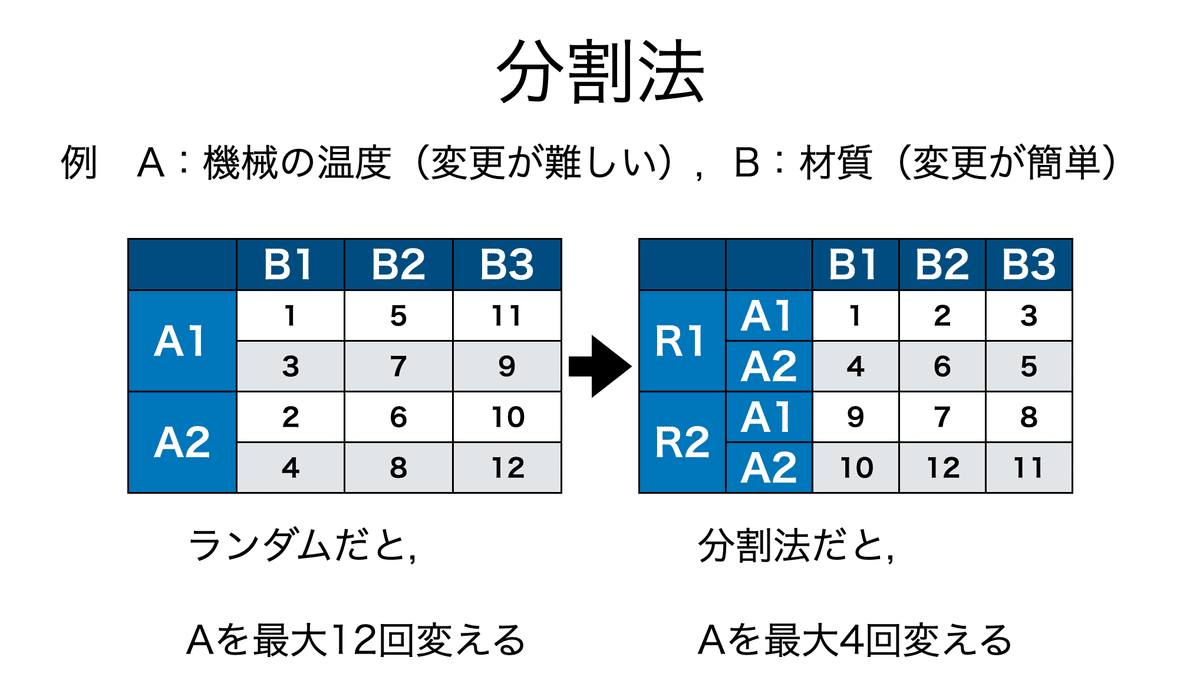
この場合，各反復ごとにブロック因子が置かれ，誤差が反復ごとのものと測定ごとのものに分解される。

また，ある水準ごとに測定を繰り返して次の水準に，という方法も分割法に含まれる。しかしこの場合は交互作用と一次誤差は交絡してしまうので，誤差を推定するには交互作用がないと仮定する必要がある。

今回は実施しないが，乱塊法や分割法の区間推定ではウェルチ–サタスウェイトの式による自由度が必要になる。

解答

グラフではAもBも差がありそうだが，問題は誤差をどう評価するか。

実際の計算では，どの要因をどの誤差で検定するかが重要になってくる。この場合，R・Aは1次誤差，B・A×Bは2次誤差で検定する。実際に効果があったのはBだけであり，Aが見かけ上効果があったのは反復による誤差と捉えることができる。

(2)について，測定の繰り返しという前提がなければ普通の二元配置であることに注意。

この場合は，A×Bはないと仮定してE1とみなして検定を行う。測定の繰り返しでは，ランダムな順番でない分の誤差を評価する必要がある。

ウェルチ–サタスウェイトの式の導出には，カイ二乗分布による近似が鍵となる。

本記事のもくじはこちら：