
書記が数学やるだけ#835 複比の不変性によるデザルグの定理
射影幾何における複比の不変性を示し,これをデザルグの定理の証明に用いる。
問題

説明
複比とは,4つの共線上の点特に射影直線上の点の集合に関連付けられた数値であり,4つの同一線上の点の唯一の射影不変量である。

解答
複比について,a3とa4がa1とa2で決定される場合の補題を示しておく。

これを用いて複比は射影変換により不変であることが示せる。

4つの線束についても複比の不変性が成り立つ。

このことを用いてデザルグの定理(P1,P2が直線mにあるなら,P3も直線mにある)を証明する。
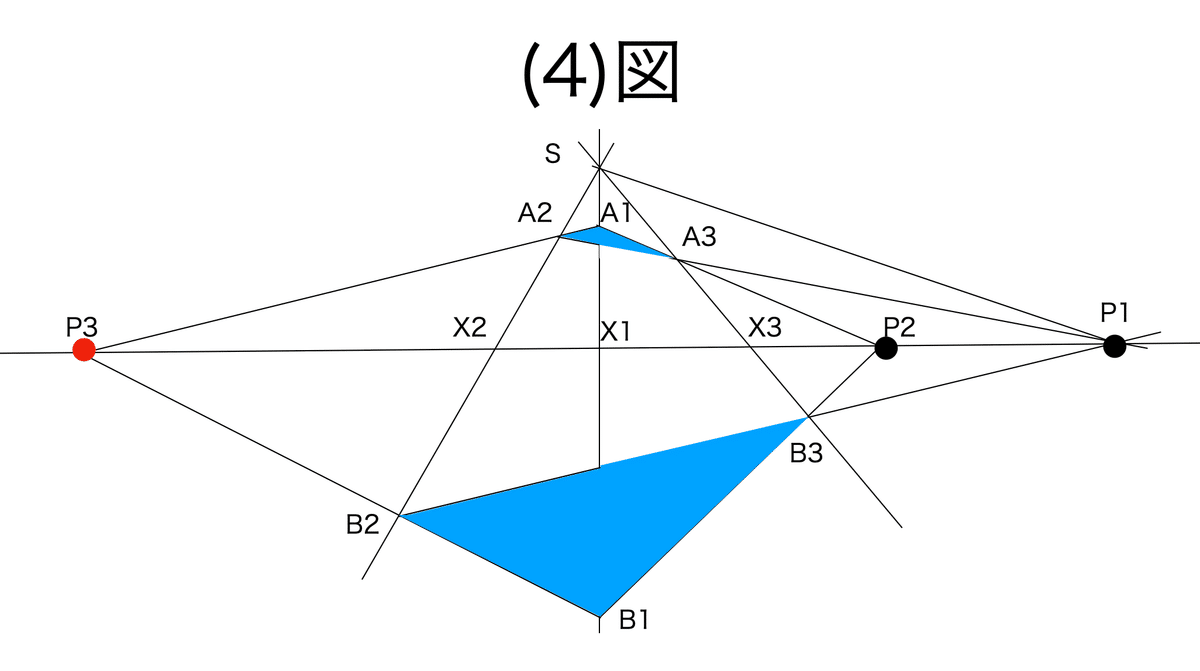
以下の青線を線束とおくと,赤線・紫線との交点について複比の不変性が成り立つ。

別の取り方により,2つ目の等式が導出できる。

よってP3はmにあることがわかる。


本記事のもくじはこちら:
学習に必要な本を買います。一覧→ https://www.amazon.co.jp/hz/wishlist/ls/1XI8RCAQIKR94?ref_=wl_share
