書記が数学やるだけ#821 多重解像度解析

ウェーブレット関数に加えスケーリング関数も含めた多重解像度解析について概要を見ていく。

問題

説明

多重解像度解析（MRA）では，スケーリング関数で基底展開された信号列を，半分の解像度のスケーリング関数とウェーブレット関数による基底展開の和に分解する。

基底展開では射影作用素を用いる：

スケーリング関数とウェーブレット関数の間には，トゥースケール関係が成り立っている。

解答

多重解像度表現について，直和分解により信号空間の階層的分解・並列分解が得られる。

並列分解に射影をかけることで，元の信号を近似成分と詳細成分に分解できる。

例としてハール関数による多重解像度表現を示す。まずはスケーリング係数などを求める。なお，ウェーブレット係数は前回求めた通り：

有限時間区間における多重解像度表現について，以下のように示せることから，近似成分と詳細成分を逐次的に求めることができる。

具体的に，近似成分と詳細成分の和が次の近似成分となる。

実装例として，1次元信号の多重解像度表現を示す。

import numpy as np
import matplotlib.pyplot as plt
import pywt

# 信号の生成
t = np.linspace(0, 1, 2**7, endpoint=False)
signal = (
    np.sin(2 * np.pi * 5 * t) +
    np.sin(2 * np.pi * 20 * t)
)

# Haarウェーブレット変換 (多重解像度解析)
coeffs = pywt.wavedec(signal, 'haar', level=4)

# 各レベルの近似成分と詳細成分
approximations = [coeffs[0]] + coeffs[1:]

# 可視化
plt.figure(figsize=(10, 6))

# オリジナル信号
plt.subplot(5, 1, 1)
plt.plot(signal)
plt.title('Original Signal')
plt.xlabel('Sample Index')
plt.ylabel('Amplitude')

# 近似成分と詳細成分
for i in range(4):
    plt.subplot(5, 1, i + 2)
    plt.plot(approximations[i], label=f'Level {i + 1} Approximation')
    plt.plot(coeffs[i + 1], label=f'Level {i + 1} Detail')
    plt.title(f'Level {i + 1}')
    plt.xlabel('Sample Index')
    plt.ylabel('Amplitude')
    plt.legend()

plt.show()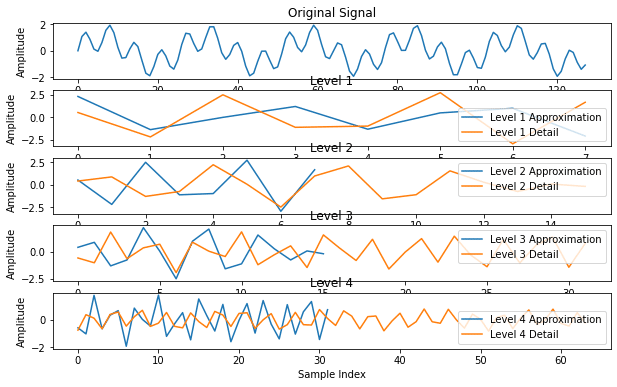

2次元の画像データについては以下の通り。

import numpy as np
import matplotlib.pyplot as plt
import pywt
from skimage import data

# 画像の読み込み
image = data.camera()

# Haarウェーブレット変換 (2次元)
coeffs2d = pywt.dwt2(image, 'haar')

# 近似成分と詳細成分
approximation = coeffs2d[0]
horizontal_detail = coeffs2d[1][0]
vertical_detail = coeffs2d[1][1]
diagonal_detail = coeffs2d[1][2]

# 可視化
plt.figure(figsize=(10, 6))

plt.subplot(2, 2, 1)
plt.imshow(approximation, cmap='gray')
plt.title('Approximation')

plt.subplot(2, 2, 2)
plt.imshow(horizontal_detail, cmap='gray')
plt.title('Horizontal Detail')

plt.subplot(2, 2, 3)
plt.imshow(vertical_detail, cmap='gray')
plt.title('Vertical Detail')

plt.subplot(2, 2, 4)
plt.imshow(diagonal_detail, cmap='gray')
plt.title('Diagonal Detail')

plt.show()

本記事のもくじはこちら：