
東京パラリンピック2020のエンブレムをpythonで描く

エンブレムに底流する1:2:√3
まず、制作の背景を紹介します。

この図形は、小中大3つの四角形からできていますが、それらの面積比が1:√3:2となっていることが発表されています。これ以降は、この3つの四角形をそれぞれP, Q, Rと呼ぶことにします。P, Q, Rはいずれも、同じ大きさの正十二角形の頂点を結んで作られたものであると考えられています。具体的には、頂点をA_0~A_11としたときに、A_0, A_1, A_6, A_7を結んでできるのがP, A_0, A_2, A_6, A_8を結んでできるのがQ, A_0, A_3, A_6, A_9を結んでできるのがRです。

したがって、エンブレムに含まれる45の四角形について、それぞれの元になっている正十二角形を全て描くことで、エンブレムの構造をより正確に把握することができます。

なお、色も単なる藍色ではなく、1:2:√3の比にあやかってCMYK表示でK=50, C=100, M=86と表される藍色が使われているということで、これをRGB表示に変換したR=0, G=17, B=127 (16進数表示で "#00117F" ) という数値で塗りつぶしの色を指定しています。
描き方の方針
さて、それではどのようにこの図形を描いていくか、に話を移しましょう。P, Q, Rの3つの四角形がそれぞれ18, 18, 9個ずつ使われてできているのがパラリンピックのエンブレムですが、どのように並んでいるかを把握するために、最も外側に位置するPに着目します。

最下部に扇型のように並んでいる5つを除いた、左右5つずつのPを見てください。右の5つのPを上から P1, P2, P3, P4, P5 としましょう。P1から始めて、P1につながっているQ, そのQにつながっているR, そのRにつながっている(内側の)Q, そのQにつながっているP, の合計5つの四角形を、まとめて一つのグループG1とみなしましょう。P2から同様に時計回りにつながっている図形を辿っていくと、P2→Q→R→Q→Qとなります。ここでは、G1と同じ並びになっているところまで、すなわち最後のQを除いたP2, Q, R, Qの4つの四角形をグループG2とします。以降も同様に、G3 (P3, Q, R), G4 (P4, Q), G5 (P5) を考えます。したがって、これらのグループG1~G5に関しては「最も外側にあるPから5つの正十二角形を (up()の状態で) 描き連ね、その途中途中で一部の頂点だけを実線で塗っていく」「最も外側の正十二角形を描き始めた場所に戻る」「一つ隣の最も外側の正十二角形の場所に移る」を繰り返せば描けることがわかります。

左の最も外側にある5つのP (下からP1'~P5'としましょう) から始まるグループ (G1'~G5') に対しても、同じ描き方が通用します。さらに、左の最も上にあるP (P5') とP1の間に、up()の状態でもう一つPが描かれていると考えれば、forループを11周させることでそれらを一気に描くことができるだろう、という方針で進めています。

残りについても、最下部に扇型のように並んでいる5つのP (P6~P10としましょう) に対して、5, 4, 3, 2, 1つの四角形からなるグループ (G6~G10) をとれば似たように描けるはずです。今回は、あえてグループのとり方を逆回り、すなわち反時計回りにします。理由は、簡潔にまとめると、G1'-5', G1-5の描き終わりとG6-10の描き始めは近い方が楽であり、角度調整を考慮し直すよりright, leftを完全に入れ替える方が楽だからです。

以上の方針に基づいて、コードを書いていきます。
プログラム全体の構成
from turtle import *
def draw12_l(a):
pos_list = []
for i in range(12):
pos_list.append(pos())
forward(a)
left(30)
pos_lists.append(pos_list)
def draw12s_r(a,n):
# 塗りつぶしたくない場合
if n == 0:
up()
draw12_l(a)
down()
n += 1
# 通常の場合
else:
for i in range(n):
up()
# 始点の移動と角度調整;iが0のときは移動不要
if i != 0:
right(30)
goto(pos_lists[i-1][6])
# 正十二角形の頂点の座標のリスト(pos_list)をリストのリスト(pos_lists)に追加
draw12_l(a)
down()
# 四角形を塗りつぶす
begin_fill()
goto(pos_lists[i][i+1])
goto(pos_lists[i][6])
goto(pos_lists[i][i+7])
goto(pos_lists[i][0])
end_fill()
# 次のグループの始点への移動と角度調整
up()
goto(2*pos_lists[0][6][0] - pos_lists[0][1][0], 2*pos_lists[0][6][1] - pos_lists[0][1][1])
down()
left(30 * (n-2))
def draw12_r(a):
pos_list = []
for i in range(12):
pos_list.append(pos())
forward(a)
right(30)
pos_lists.append(pos_list)
def draw12s_l(a,n):
# 塗りつぶしたくない場合(今回は生じない)
if n == 0:
up()
draw12_r(a)
down()
n += 1
# 通常の場合
else:
for i in range(n):
up()
# 始点の移動と角度調整;iが0のときは移動不要
if i != 0:
left(30)
goto(pos_lists[i-1][6])
# 正十二角形の頂点の座標のリスト(pos_list)をリストのリスト(pos_lists)に追加
draw12_r(a)
down()
# 四角形を塗りつぶす
begin_fill()
goto(pos_lists[i][i+1])
goto(pos_lists[i][6])
goto(pos_lists[i][i+7])
goto(pos_lists[i][0])
end_fill()
# 次のグループの始点への移動と角度調整
up()
goto(pos_lists[0][1])
down()
right(30 * (n-2))
pencolor('#00117F')
fillcolor('#00117F')
left(60)
for j in range(11):
pos_lists = []
draw12s_r(15,5-j%6)
left(30)
for j in range(5):
pos_lists = []
draw12s_l(15,5-j%6)このプログラムは、主に4つの関数 A) draw12_l, B) draw12s_r, C) draw12_r, D) draw12s_l から成っています。A, B は G1'-5' および G1-5 を描くための関数で、C, D は G6-10 を描くための関数です。
イメージとしては図の通りです。まず、A) draw12_l ;「正十二角形をforward→leftの繰り返しで描く」関数を用いて、B) draw12s_r ;「いくつかの正十二角形を少しずつ右にずれていく形で繋げて描く関数」を定義します。次に同様に、C) draw12_r ;「正十二角形をforward→rightの繰り返しで描く」関数を用いて、D) draw12s_l ;「いくつかの正十二角形を少しずつ左にずれていく形で繋げて描く関数」を定義します。最後に、Bを11回繰り返すことで黄色の領域 (G1'-5' および G1-5) を描いたあと、Dを5回繰り返すことで緑色の領域 (G6-10) を描くという流れです。

なお、動きの対称性から、C) draw12_r は A) draw12_l 内の left を right に書き換えることで、D) draw12s_l は B) draw12s_r 内の right, left を入れ替えて最後のgoto()内を調整することで完成します。また、正十二角形の大きさを 15cm としています。
A) draw12_l
def draw12_l(a):
pos_list = []
for i in range(12):
pos_list.append(pos())
forward(a)
left(30)
pos_lists.append(pos_list)この関数で行っていることは、1) 各頂点に到着した際に座標を pos_list というリストに保存しながら、2) 1辺の長さが a である正十二角形を下図のように反時計回りに描き、3) 最後に pos_list を pos_lists というリストに保存することです。pos_listsについては次の関数内で説明します。
なお、C) draw12_r は同じことを逆回りで行う (始点から時計回りに11の頂点を辿って始点に戻る) だけなので、説明を割愛します。

B) draw12s_r
def draw12s_r(a,n):
# 塗りつぶしたくない場合
if n == 0:
up()
draw12_l(a)
down()
n += 1
# 通常の場合
else:
for i in range(n):
up()
# 始点の移動と角度調整;iが0のときは移動不要
if i != 0:
right(30)
goto(pos_lists[i-1][6])
# 正十二角形の頂点の座標のリスト(pos_list)をリストのリスト(pos_lists)に追加
draw12_l(a)
down()
# 四角形を塗りつぶす
begin_fill()
goto(pos_lists[i][i+1])
goto(pos_lists[i][6])
goto(pos_lists[i][i+7])
goto(pos_lists[i][0])
end_fill()
# 次のグループの始点への移動と角度調整
up()
goto(2*pos_lists[0][6][0] - pos_lists[0][1][0], 2*pos_lists[0][6][1] - pos_lists[0][1][1])
down()
left(30 * (n-2))この関数で行っていることは、1) いくつかの正十二角形から成る一つのグループを描き、2) 次のグループの書き始めの点まで移ることです。引数 a, n にはそれぞれ、正十二角形の辺の長さと、グループに含まれる正十二角形の個数をとります。詳しく見ていきます。
# 塗りつぶしたくない場合
if n == 0:
up()
draw12_l(a)
down()
n += 1まず、最初のif文では一つも塗りつぶしたくない場合 (G5' と G1 の間を通過する際) について書いています。この場合も、次のグループの始点を指定するために一つ目の正十二角形の座標が必要なので、ペンを上げた状態で一つだけ正十二角形を描くことにしています。最後に n += 1 がついている理由は、角度調整を正しく行うためです。角度の状態としては、一つの正十二角形を描き終わったときと同じなので、最終行の left(30 * (n-2)) にそのまま代入できるように n を1にしておく必要があるためです。n = 0 のままにしておくと、G1 の描き始めが 30° だけ右にずれてしまい、形が崩れることになります。
# 通常の場合
else:
for i in range(n):
up()
# 始点の移動と角度調整;iが0のときは移動不要
if i != 0:
right(30)
goto(pos_lists[i-1][6])
# 正十二角形の頂点の座標のリスト(pos_list)をリストのリスト(pos_lists)に追加
draw12_l(a)
down()通常 (G5' と G1 の間を通過する際以外) は、全ての正十二角形を描き終えるまでに、1) 正十二角形を空で描いて座標を記憶、2) そのうち4頂点を選んで塗りつぶす、3) 隣の正十二角形の始点に移る を繰り返すことになります。
まず頂点を命名します。1個目の正十二角形の頂点を A_0 ~ A_11 とし、2個目以降は B_0 ~ B_11, C_0 ~ C_11, ... と命名することにします。ただし、各十二角形の始点 (A_0, B_0, C_0, ...) の位置を定める必要があります。共有辺上だと位置がわかりやすく、塗りつぶしで使用する頂点に始点があれば他頂点の数値を指定しやすいことから、図のように設定することにします。
このとき、2個目の正十二角形はA_6をB_0として描けばよく、3個目以降も同様 (B_6→C_0, C_6→D_0, ...) です。描き始めの角度は 30° ずつ右に回転するので、「m+1 個目の正十二角形は、 m 個目の正十二角形の 6 番の頂点を始点 ( 0 番の頂点 ) として、m 個目を描き始めたときより右に 30° だけ回転させた角度で描き始める」…(*)とまとめることができます。これを反映しているのが、上記コードの4-6行目です ( i = 0 のときは描き始めで移動が不要なので if i != 0としています)。なお、pos_lists は pos_list を要素とするリストであり、[[A_0の座標, A_1の座標, ..., A_11の座標], [B_0の座標, B_1の座標, ..., B_11の座標], [], [], ...] という構造になっているので、pos_lists[i-1][6]は一つ前の正十二角形の 6 番の頂点の座標を取り出していることになります。

# 四角形を塗りつぶす
begin_fill()
goto(pos_lists[i][i+1])
goto(pos_lists[i][6])
goto(pos_lists[i][i+7])
goto(pos_lists[i][0])
end_fill()塗りつぶす四角形の4頂点を考えます。図を参考にすれば、2頂点はどの i のときでも 0, 6番の頂点で、残り2つは i+1, i+7番の頂点なので、それらを順に巡るようにgotoメソッドを連ねてbegin_fill(), end_fill()で囲います。
# 次のグループの始点への移動と角度調整
up()
goto(2*pos_lists[0][6][0] - pos_lists[0][1][0], 2*pos_lists[0][6][1] - pos_lists[0][1][1])
down()
left(30 * (n-2))最後に、入れ子になっている if 文の外側、すなわち最後の4行について説明します。この箇所では、次のグループを描き始められる状態にするために、座標と角度を変更しています。
座標については、両グループで最初に描く正十二角形の両方と辺を共有する2つの正十二角形を考えることでわかります。先に描いたグループで2番目に描いたもの (内側) と、その外側に位置するものの2つが条件を満たしますが、このうち外側の方に、先に描いたグループで最初に描いたPを平行移動して描き足します。すると、そのPの1頂点が次のグループの始点 (下図では矢印の位置) となることがわかります。つまり、先に描いたグループの1個目の正十二角形の頂点A_6 (x_6, y_6) は、A_1 (x_1, y_1) と次のグループの始点 (xx, yy) の中点になっているわけです。x 座標, y 座標についてこれを整理すれば xx = 2x_6 - x_1, yy = 2y_6 - y_1 となり、次のグループの始点の座標を先に描いたグループにおける座標で表すことができます (pos_lists[0][6] = (x_6, y_6) (タプル形式) であることに注意)。

角度については、順を追って考えます。グループで n 個の正十二角形を描き終えた場合、n個目を描き終えた際の角度はn個目を描き始めた際の角度と同じなので、1個目を描き始めた際から考えると右に 30° ずつ n-1 回だけ回転しています。また、次のグループの描き始めの角度は、先に描いたグループの描き始めの角度から右に 30° だけ回転しています (12個のPが外周に並ぶことから考えるとかりやすいです)。以上のことから、左に 30*(n-1-1)° だけ回転させれば角度が合います。
D) draw_12s_l
def draw12s_l(a,n):
# 塗りつぶしたくない場合(今回は生じない)
if n == 0:
up()
draw12_r(a)
down()
n += 1
# 通常の場合
else:
for i in range(n):
up()
# 始点の移動と角度調整;iが0のときは移動不要
if i != 0:
left(30)
goto(pos_lists[i-1][6])
# 正十二角形の頂点の座標のリスト(pos_list)をリストのリスト(pos_lists)に追加
draw12_r(a)
down()
# 四角形を塗りつぶす
begin_fill()
goto(pos_lists[i][i+1])
goto(pos_lists[i][6])
goto(pos_lists[i][i+7])
goto(pos_lists[i][0])
end_fill()
# 次のグループの始点への移動と角度調整
up()
goto(pos_lists[0][1])
down()
right(30 * (n-2))これはほとんど B) draw_12s_r と同じですが、rightとleftを入れ替えているほか、最後から3行目にてgotoメソッドで指定している移動先が異なります。これは、先に描いたグループの正十二角形のA_1を次のグループの始点 (A_0) とするためです。なお、正十二角形の頂点の順番が逆回り (反時計回り) になっていることに注意が必要です。
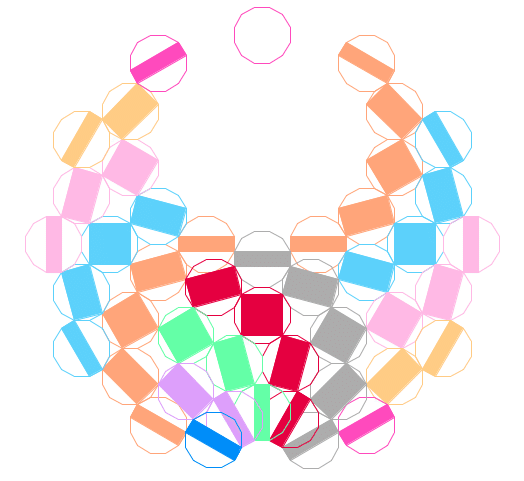
実行部分
pencolor('#00117F')
fillcolor('#00117F')
left(60)
for j in range(11):
pos_lists = []
draw12s_r(15,5-j%6)
left(30)
for j in range(5):
pos_lists = []
draw12s_l(15,5-j%6)色指定に関しては前述の通りです。また、turtleではデフォルトの描き始めが右向きなので、4行目のように left(60) で G1' の描き始めの角度に合わせます (図参照)。
5-7 行目の forループでは、G1' (j=0,n=5), G2' (j=1,n=4), G3' (j=2,n=3), G4' (j=3,n=2), G5' (j=4,n=1), φ(j=5,n=0), G1 (j=6,n=5), G2 (j=7,n=4), G3 (j=8,n=3), G4 (j=9,n=2), G5(j=10,n=1) を描いています (nはグループ内の正十二角形の個数)。draw12s_r(a,n)の引数nに、j を6で割った余りを5から引いた値をとれば、if文を使わずに上記の通り簡潔にまとめることができます。

8行目の left(30) は、少し驚きかもしれません。B) draw_12s_r を終えた時点での角度と位置を考えるにあたり、角度はわかりやすいの (真上) ですが、位置が実はちょうど G6 の始点にあたるのというのはわかりにくいです。
そこで、G5 の次の架空の正十二角形を描いた上で、8行目の前に forward(15) を入れて描いたものと比較しましょう。なお、上に 1 辺分進める理由は、これを行った場合に、Turtle は逆回りで描く場合に架空の正十二角形を描く始点となる場所からみて6つ先 (つまり180°逆のところ) の頂点に移ることになるので、left(30) を行った上で G6 の描画に入ると今までと同様の配置になるからです。
これを見ると、G6-10 の領域とそれ以外の領域の間に少しの隙間が生じています。なぜ隙間が生じたかというと、今までの流れを汲めば現在何も入っていない正十二角形には P が入るはずで、現在の G6 における 1-3 個目には P, Q, R ではなくQ, R, Q が入るはずだったからです。QがPになったことで8番にあった四角形の1頂点が7番に移り、RがQになったことで9番にあった四角形の1頂点が8番に移り…という変化が起きているので、その隙間を埋めるには1辺分だけ下げる必要があります。G6の始点の段階でこの調整をしておけば良いので、先ほどの forward(15) を消せばうまくいくことが感覚的にもわかると思います。

最後の forループに関しては、4-7 行目の forループと基本的には同じ原理なので、説明は割愛します。
ソースコード (再掲) と完成図
以上の内容をまとめたコードがこちらになります。これを動かすと、東京パラリンピック2020のエンブレムが完成します。
from turtle import *
def draw12_l(a):
pos_list = []
for i in range(12):
pos_list.append(pos())
forward(a)
left(30)
pos_lists.append(pos_list)
def draw12s_r(a,n):
# 塗りつぶしたくない場合
if n == 0:
up()
draw12_l(a)
down()
n += 1
# 通常の場合
else:
for i in range(n):
up()
# 始点の移動と角度調整;iが0のときは移動不要
if i != 0:
right(30)
goto(pos_lists[i-1][6])
# 正十二角形の頂点の座標のリスト(pos_list)をリストのリスト(pos_lists)に追加
draw12_l(a)
down()
# 四角形を塗りつぶす
begin_fill()
goto(pos_lists[i][i+1])
goto(pos_lists[i][6])
goto(pos_lists[i][i+7])
goto(pos_lists[i][0])
end_fill()
# 次のグループの始点への移動と角度調整
up()
goto(2*pos_lists[0][6][0] - pos_lists[0][1][0], 2*pos_lists[0][6][1] - pos_lists[0][1][1])
down()
left(30 * (n-2))
def draw12_r(a):
pos_list = []
for i in range(12):
pos_list.append(pos())
forward(a)
right(30)
pos_lists.append(pos_list)
def draw12s_l(a,n):
# 塗りつぶしたくない場合(今回は生じない)
if n == 0:
up()
draw12_r(a)
down()
n += 1
# 通常の場合
else:
for i in range(n):
up()
# 始点の移動と角度調整;iが0のときは移動不要
if i != 0:
left(30)
goto(pos_lists[i-1][6])
# 正十二角形の頂点の座標のリスト(pos_list)をリストのリスト(pos_lists)に追加
draw12_r(a)
down()
# 四角形を塗りつぶす
begin_fill()
goto(pos_lists[i][i+1])
goto(pos_lists[i][6])
goto(pos_lists[i][i+7])
goto(pos_lists[i][0])
end_fill()
# 次のグループの始点への移動と角度調整
up()
goto(pos_lists[0][1])
down()
right(30 * (n-2))
pencolor('#00117F')
fillcolor('#00117F')
left(60)
for j in range(11):
pos_lists = []
draw12s_r(15,5-j%6)
left(30)
for j in range(5):
pos_lists = []
draw12s_l(15,5-j%6)
参考資料
・Python公式ドキュメント turtle(https://docs.python.org/ja/3/library/turtle.html#turtle.end_fill)
+ 塗りつぶしの方法および、その色のRBG表記による指定
+ 線の色のRGB表記による指定
・第27回モリサワ文字文化フォーラム [個と群と律] 組市松紋の仕組み 2019年6月27日 株式会社モリサワ(https://www.morisawa.co.jp/culture/forums/reports/4632)
+ エンブレムの正確な幾何学的な形状
+ エンブレムに使用された色
・2020年東京オリンピック 野老さんの新エンブレムの解析/正12角形からなる幾何的デザインの構成の解析 鱈本父(@tsatie)(https://www.evernote.com/shard/s18/sh/3b028194-d8ae-47af-a4d6-cbd1322025cb/4454e16651b14b8d2a6778cd08d4c0b1/res/5958ad7b-9147-4b81-9721-13075b1c40c7/20160501LuaTeXMetaPostOlympicEmblemReport.pdf)
+ エンブレムを描く手順
